Уравнения в полных диффернциалах

Интегрирующий множитель

Определение 12.13.

Дифференциальное уравнение 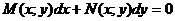называется уравнением в полных дифференциалах, если его левая часть есть полный дифференициал некоторой функции 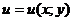, то есть .

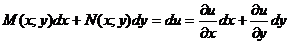Уравнение в полных дифференциалах может быть переписано в виде 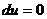, так что его общий интеграл имеет вид .

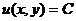Теорема 12.3.

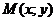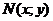Пусть функция и определены и непрерывны в некоторой области D и имют в ней непреывные частные производные соответственно по у и по х. Тогда, для того чтобы уравнение 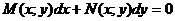было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество .

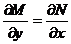При выполнении этого условия общий интеграл можно записать в виде 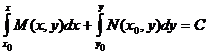или 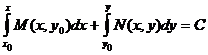, где нижние пределы х_0,,у₀ можно выбрать произвольно, лишь бы точка (х₀,у₀) D.

Особых решений уравнение в полных дифференциалах не имеет.

Пример 12.14.

Проинтегрируем дифференциальное уравнение .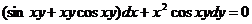

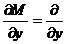
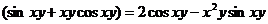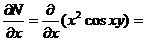
Проверим, является ли оно уравнением в полных дифференциалах: , , 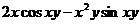так что .

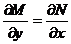Таким образом, имеем уравнение в полных дифференциалах.

Общее решение определим по формуле 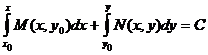, взяв за начальную точку 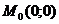: 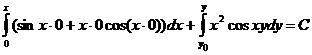. Интегрируя, получим xsinxy = C. Это и есть общий интеграл данного дифференциального уравнения.

Укажем другой способ нахождения общего интеграла уравнения в полных дифференциалах.

Функция 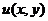должна удовлетворять системе уравнений . (*)

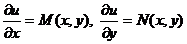Интегрируя частным образом по х первое из уравнений (*), получим 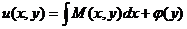, где φ(у) – произвольная дифференцируемая функция от у. Выберем ее так, чтобы функция 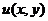была решением и второго из уравнений (*).

Дифференцируя 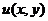по у и полагая 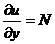, для нахождения φ(у) получаем дифференциальное уравнение вида φ(у')=ω(у), интегрируя которое, найдем функцию .

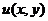Пример 12.15.

Найдем общий интеграл уравнения в полных дифференциалах .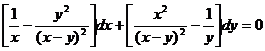

Интегрируя по х коэффициент при dx, получим 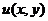= 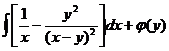или = .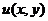

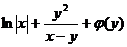Дифференцируя по у и приравнивая коэффициенту при dy, находим 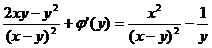, откуда 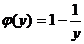, а тогда .

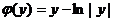Определив функцию 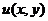и полагая u=С, найдем общий интеграл .

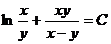Определение 12.14.

Функция 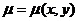называется интегрирующим множителем, если дифференциальное уравнение 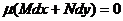есть уравнение в полных дифференциалах.

Интегрирующий множитель можно найти из уравнения с частными производными .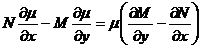

Пусть уравнение 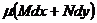= 0 имеет интегрирующий множитель, заисящий только от х, тогда .(**)

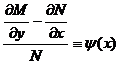В этом случае 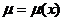есть решение уравнения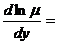 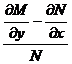. Оно имеет вид .

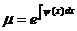Если уравнение 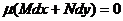имеет интегрирующий множитель, зависящий только от у, то .

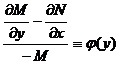Множитель 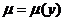ищется как решение уравнения . (***)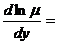

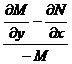Оно имеет вид .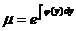

Пример 12.16.

Решим дифференциальное уравнение .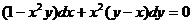

Легко показать, что оно не является уравнением в дифференциалах.

Проверим, не имеет ли оно интегрирующего множителя, зависящего только от х.

Имеем 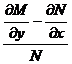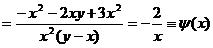, то есть условие (**) выполнено. Поэтому .

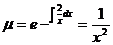Умножая обе части исходного уравнения на 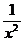, получим 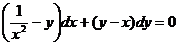- уравнение в полных дифференциалах.

Найдем его общий интеграл: 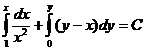, или .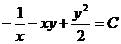

Пример 12.17.

Решим дифференциальное уравнение .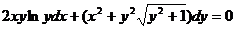

Здесь 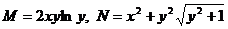. Условие теоремы 12.3 не выполнено.

Имеем 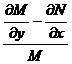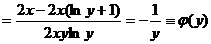, следовательно, по условию (***)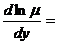 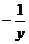, откуда .

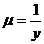Уравнение 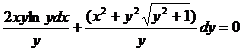является уравнеием в полных дифференциалах, общее решение которого .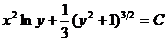