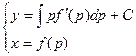Уравнения в полных дифференциалах (тотальные)

Определение. Дифференциальное уравнение первого порядка вида:

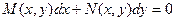
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции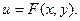

Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде: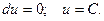

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;

2) как найти эту функцию.

Если дифференциальная форма 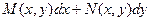является полным дифференциалом некоторой функции u, то можно записать:

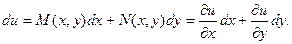
Т.е. .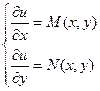

Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:

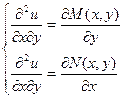
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.

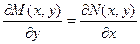
Теперь рассмотрим вопрос о нахождении собственно функции u.

Проинтегрируем равенство :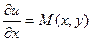

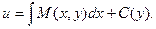
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром.

Определим функцию С(у).

Продифференцируем полученное равенство по у.

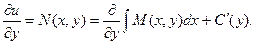
Откуда получаем: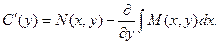

Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.

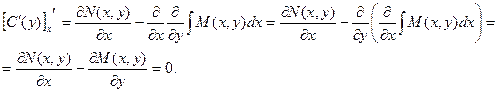
Теперь определяем функцию С(у):

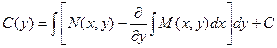
Подставляя этот результат в выражение для функции u, получаем:

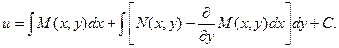
Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

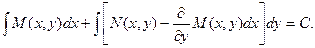
Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.

Пример. Решить уравнение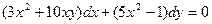

Проверим условие тотальности: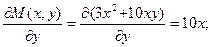

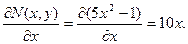
Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию u.

;

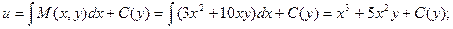
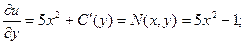
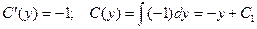Итого,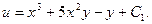

Находим общий интеграл исходного дифференциального уравнения:

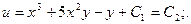
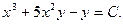
Уравнения вида y = f(y’) и x = f(y’).

Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции.

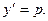
Для уравнения первого типа получаем: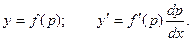

Делая замену, получаем: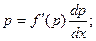

В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.

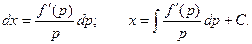
Общий интеграл в параметрической форме представляется системой уравнений:

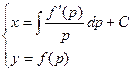
Исключив из этой системы параметр р, получим общий интеграл и не в параметрической форме.

Для дифференциального уравнения вида x = f(y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат: