Уравнения в полных дифференциалах
Пусть Р = Р(х, у) и Q = Q(х, у) – непрерывные функции. Уравнение вида
P dx + Q dy = 0 (10)
называется уравнением в полных дифференциалах , если
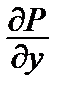 =
= 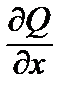 .
.
Уравнение (10) тогда и только тогда является уравнением в полных дифференциалах, когда существует функция U = U(х, у) такая, что
dU = P dx + Q dy ,
т.е.
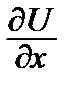 = P,
= P, 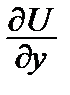 = Q. (11)
= Q. (11)
Общий интеграл уравнения (10) имеет вид
U(х, у) = С.
ЗАДАЧИ
1. Решить дифференциальные уравнения. Найти частный интеграл, если заданы начальные
условия:
1.1. 2x cos2y dx + (2y – x2sin 2y) dy = 0 .
Р е ш е н и е. Здесь P = 2x cos2y, Q = 2y – x2sin 2y.
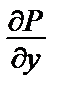 = –4x cos y sin y = –2x sin 2 y,
= –4x cos y sin y = –2x sin 2 y, 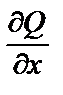 = –2x sin 2 y.
= –2x sin 2 y. 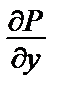 =
= 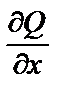 => исходное уравнение – уравнение в полных дифференциалах. Значит, существует функция U , такая, что
=> исходное уравнение – уравнение в полных дифференциалах. Значит, существует функция U , такая, что
dU = 2x cos2y dx + (2y – x2sin 2y) dy.
Поэтому 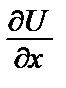 = 2x cos2y. Отсюда U =
= 2x cos2y. Отсюда U = 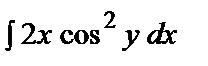 = x2 cos2y + f (y), где функция f (y) зависит только от у (постоянна по отношению к х).
= x2 cos2y + f (y), где функция f (y) зависит только от у (постоянна по отношению к х).
Дифференцируя найденную функцию по у, получим выражение
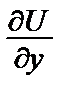 = – x2sin 2y + f ´ (y),
= – x2sin 2y + f ´ (y),
которое, согласно (11) можно приравнять к Q:
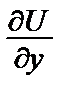 = – x2sin 2y + f ´ (y) = 2y – x2sin 2y.
= – x2sin 2y + f ´ (y) = 2y – x2sin 2y.
Отсюда f ´ (y) = 2y и f (y) = у2 – С. Т.о., U = x2 cos2y + у2 – С.
Окончательно получаем, что общий интеграл исходного уравнения равен x2 cos2y + у2 = С.
1.2. (3x2 + 2у) dx + (2x – 3) dy = 0 .
1.3. (3x2y – 4xу2) dx + (x3 – 4x2y + 12 y3) dy = 0 .
1.4. (x + 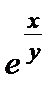 ) dx +
) dx + 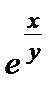 (1 –
(1 – 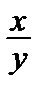 ) dy = 0 , y(0) = 2.
) dy = 0 , y(0) = 2.
3. Уравнения n-го порядка, допускающие понижение порядка
Надо знать 3 (три!) основных типов таких уравнений!
3.1. Решение дифференциального уравнения y(n) = f (x)
Для решения уравнения y(n) = f (x) сделаем замену
y(n-1) (x) = z(x), y(n) (x) = z´(x).
Тогда
z´(x) = f (x), 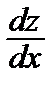 = f (x), z(x) =
= f (x), z(x) = 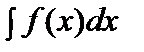 + С1.
+ С1.
Но z(x) = y(n-1) (x). Следовательно,
y(n-1) (x) = 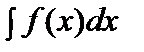 + С1.
+ С1.
Повторяя эту операцию еще (n -1) раз, получим y (x).
ЗАДАЧИ
1. Решить дифференциальные уравнения. Найти частное решение (интеграл), если заданы начальные
условия:
1.1. y(4) (x) = sin x.
Р е ш е н и е. Проинтегрируем данное уравнение 4 раза:
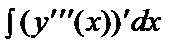 =
= 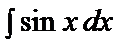 ,
,
y´´´(x) = –cos x + C1,
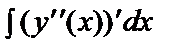 =
= 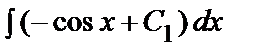 ,
,
y´´(x) = –sin x + C1 x + C2,
y´(x) = cos x + C1 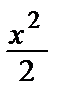 + C2 x + C3,
+ C2 x + C3,
y (x) = sin x + C1 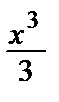 + C2
+ C2 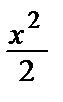 + C3 x + C4.
+ C3 x + C4.
1.2. xy(4) = 1.
1.3. y(20) (x) = sin x.
1.4. y´´= 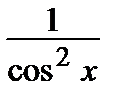 ; y
; y  =
= 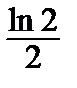 , y´
, y´  = 0.
= 0.
1.5. y´´´= 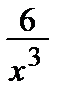 ; y(1) = 2, y´(1) = 1, y´´(1) = 1.
; y(1) = 2, y´(1) = 1, y´´(1) = 1.
3.2. Уравнения, не содержащие явно функцию y
Уравнение
y´´ = f (x, у´)
сводится к уравнению первого порядка с помощью замены y´ = z (x), y´´ = z´ (x).
ЗАДАЧИ
1. Решить дифференциальные уравнения. Найти частное решение (интеграл), если заданы начальные
условия:
1.1. x2 y´´ + x y´ = 1.
Р е ш е н и е. Уравнение не содержит явно функцию у. Сделав замену y´ = z (x), y´´ = z´ (x), получим
x2 z´ + x z = 1. (12)
Уравнение второго порядка перешло в линейное уравнение первого порядка, которое можно решить с помощью замены z = uv. Вначале приведем выражение (12) к виду y´ + p(x) y + q(x) = f (x) (делим правую и левую части на x2 (делить можно, т.к. х, очевидно, не является решением уравнения)):
z´ + 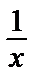 z =
z = 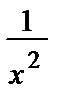 . (13)
. (13)
Имеем: z = uv, z´ = u´v + uv´ .
Подставим эти выражения в (13) и получим
u´v + uv´ + 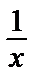 uv =
uv = 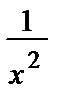 .
.
Отсюда: v (u´ + 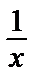 u) + uv´ =
u) + uv´ = 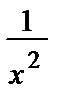 . (14)
. (14)
Приравниваем выражение в скобках к нулю:
u´ + 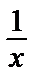 u = 0,
u = 0,
и находим u:
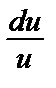 = –
= – 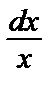 => ln|u| = ln
=> ln|u| = ln 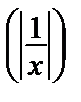 => u =
=> u = 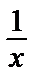 .
.
Подставляя его в (14), с учетом того, что выражение в скобках равно нулю, находим v:
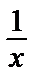 v´ =
v´ = 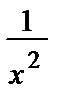 => dv =
=> dv = 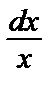 => v = ln|C1x| .
=> v = ln|C1x| .
Отсюда z = 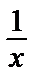 ln|C1x|.
ln|C1x|.
Т.о., возвращаясь к начальной замене, имеем еще одно дифференциальное уравнение первого порядка
y´ = 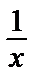 ln|C1x|,
ln|C1x|,
решая которое получим
y = 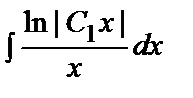 =
= 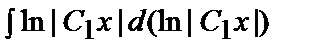 =
= 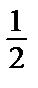 ln2|C1x| + C2.
ln2|C1x| + C2.
1.2. x2 y´´ = (y´ )2.
1.3. 2xy´y´´ = (y´ )2 – 1.
1.4. xy´´´ + y´´ = 1 + x.
1.5. xy´´´´ + y´´´ = ex.
1.6. (1 + x2) y´´ – 2xy´ = 0; y(0) = 0, y´(0) = 3.
1.7. y´´ = 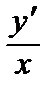
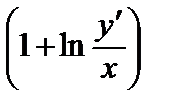 ; y(1) =
; y(1) = 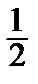 , y´(1) = 1.
, y´(1) = 1.
3.3. Уравнения, не содержащие явно х
Уравнение
y´´ = f (у, у´)
с помощью замены
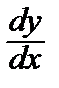 = p (y),
= p (y), 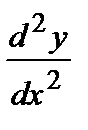 =
= 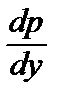 ·
· 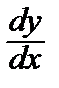 = p´ p
= p´ p
сводится к уравнению первого порядка относительно функции p (y).
ЗАДАЧИ
1. Решить дифференциальные уравнения. Найти частное решение (интеграл), если заданы начальные
условия:
1.1. y´´ + 2у y´ = 0; у(0) = 2, у´(0) = –4.
Р е ш е н и е. Уравнение не содержит явно переменную х. Сделав замену y´ = p, y´´ = p´ p, получим
уравнение первого порядка относительно p (y):
p´ p + 2ур = 0, или p´ = –2у .
Отсюда находим р:
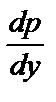 = –2у
= –2у 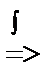
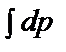 = –
= – 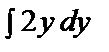 => p = –y2 + C1,
=> p = –y2 + C1,
Следовательно,
y´ = –y2 + C1, (15)
Подставив в (15) начальные данные, получим:
–4 = –4 + C1 => C1 = 0.
Отсюда
y´ = –y2 => 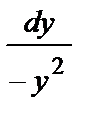 = dx
= dx 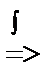
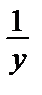 = x + C2 => y =
= x + C2 => y = 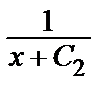 .
.
Подставляем сюда начальные данные:
2 = 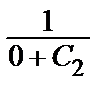 => C2 =
=> C2 = 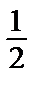 .
.
Таким образом, частное решение имеет вид
y = 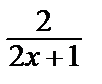 .
.
1.2. y y´´ + (y´ )2 = 0.
1.3. y3y´´ = 1; y 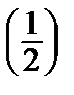 = 1, y´
= 1, y´ 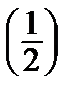 = 1.
= 1.
1.4. y´´ – (y´ )2 + y´ (y – 1) = 0; y(0) = 2, y´(0) = 2.
4. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
Общие положения
Линейным дифференциальным уравнением n-го порядка называется уравнение вида
y(n) + p1(x) y(n-1) + p2(x) y(n-2) + … + pn-1(x)y´ + pn(x)y = q(x),
где p1(x), p2(x), … , pn(x), q(x) – непрерывные функции.
При q(x) = 0 оно называется однородным, а при q(x) ≠ 0 – неоднородным.
Общее решение линейного однородного уравнения имеет вид
уобщ = 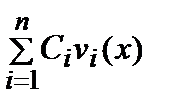 ,
,
где vi(x), i = 1, 2, … , n – линейно независимая система решений.
Общее решение линейного неоднородного уравнения имеет вид
уобщ = 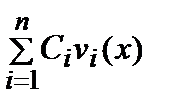 + у⃰,
+ у⃰,
где vi(x), i = 1, 2, … , n – линейно независимая система решений, соответствующая линейному
однородному уравнению;
у⃰ – частное решение неоднородного уравнения.
Линейно независимая система решений v1, v2, … , vn линейного однородного уравнения называется фундаментальной системой решений.
Наложение решений. Если правая часть линейного неоднородного уравнения
y(n) + p1(x) y(n-1) + p2(x) y(n-2) + … + pn-1(x)y´ + pn(x)y = q (х) и
представляет собой сумму двух функций
q(x) = q1(x) + q2(x),
а уч1 и уч2 – частные решения уравнений
y(n) + p1(x) y(n-1) + p2(x) y(n-2) + … + pn-1(x)y´ + pn(x)y = q1 (х) и
y(n) + p1(x) y(n-1) + p2(x) y(n-2) + … + pn-1(x)y´ + pn(x)y = q2 (х)
соответственно, то функция уч = уч1 + уч2 является решением данного уравнения.
