Ряды Тейлора и Маклорена. Разложение функций в ряд Тейлора и Маклорена
Определение 11.4
Пусть функция y=f(x) имеет в некоторой окрестности точки x0 производные любого порядка.
Ряд вида 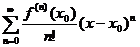 называется рядом Тейлора для функции f(x).
называется рядом Тейлора для функции f(x).
Если же для всех значений x из некоторой окрестности точки x0 ряд сходится и имеет в качестве суммы функцию f(x), то есть
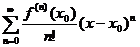 = f(x), то функция f(x) называется разложимой в ряд Тейлора в окрестности точки x0 (или по степеням x-x0).
= f(x), то функция f(x) называется разложимой в ряд Тейлора в окрестности точки x0 (или по степеням x-x0).
Если x0=0, то ряд Тейлора имеет вид
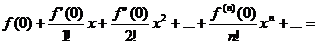
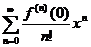 и называется рядом Маклорена для функции f(x).
и называется рядом Маклорена для функции f(x).
Теорема 11.3.
Для того чтобы функция y=f(x) была разложима в ряд Тейлора в окрестности точки x0, необходимо и достаточно, чтобы 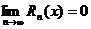 , где Rn – остаточный член формулы Тейлора (остаточный член в форме Лагранжа имеет вид
, где Rn – остаточный член формулы Тейлора (остаточный член в форме Лагранжа имеет вид 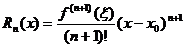 ,
, 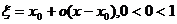 ).
).
Теорема 11.4.
Если f(x) имеет в некотором промежутке, содержащем точку x0, производные всех порядков, для которых |f(n)(x)|≤M, то функция f(x) разложима в этом промежутке в ряд Тейлора.
При разложении функции f(x) в ряд Тейлора применяют следующие приемы:
1. Непосредственное разложение f(x) в ряд Тейлора, которое состоит из трех этапов:
а) формально составляют ряд Тейлора, для чего находят f(n)(x) для любых n, вычисляют f(n)(x0) и подставляют найденные значения в ряд;
б) находят область сходимости ряда Тейлора;
в) выясняют, для каких значений x из области сходимости ряда
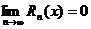 , то есть, для каких x имеет место равенство:
, то есть, для каких x имеет место равенство:
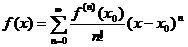
2. Использование готовых разложений в ряд Маклорена:
а) 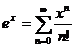
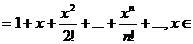 /R;
/R;
б) 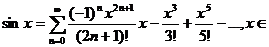 /R;
/R;
в) 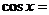
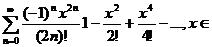 /R;
/R;
г) 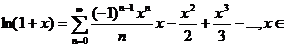 /R;
/R;
|
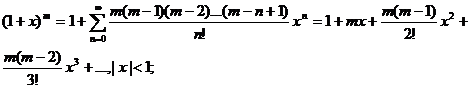
е) 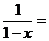
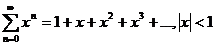 ;
;
ж) 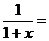
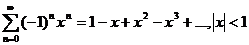 ;
;
Пример 11.6.
Разложим функцию  в ряд Тейлора в окрестности точки x=2. Решим эту задачу двумя способами.
в ряд Тейлора в окрестности точки x=2. Решим эту задачу двумя способами.
I способ.
Используем непосредственное разложение функции в ряд Тейлора:
 ;
;
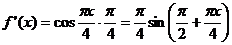 ;
;
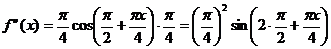
……………………………………………...
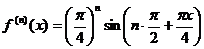
……………………………
Вычислим найденные производные в точке x=2:
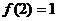
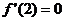
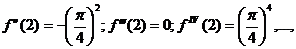
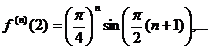 .
.
Составим формально ряд Тейлора:
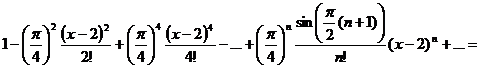
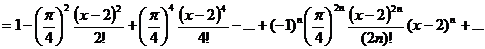 .
.
Найдем область сходимости ряда, используя признак Даламбера:
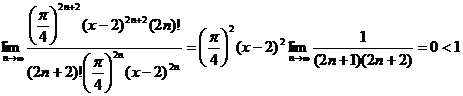 .
.
Этот результат будет справедлив при любых x, следовательно, данный ряд сходится на всей числовой оси, то есть 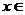 /R.
/R.
Докажем, что при всех x ряд сходится к 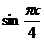 , для чего достаточно показать, что
, для чего достаточно показать, что 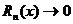 при
при 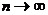 :
:
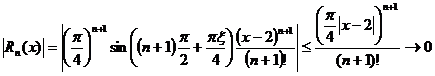 при
при 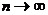 .
.
Как результат решения задачи можем записать:
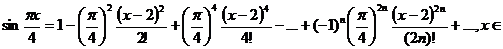 /R.
/R.
II способ.
Разложим  в ряд Тейлора в окрестности точки x=2, используя готовое разложение.
в ряд Тейлора в окрестности точки x=2, используя готовое разложение.
Преобразуем 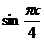 следующим образом:
следующим образом:
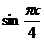
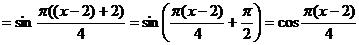 .
.
В ряд Маклорена для cosx (формула в)) справа и слева вместо x подставим 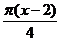 , тогда получим:
, тогда получим:
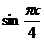
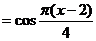
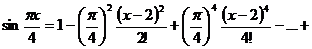
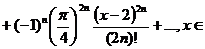 /R.
/R.
При разложении функции в ряд часто используют почленное дифференцирование и интегрирование рядов.
Пример 11.7.
Разложить в ряд Маклорена функцию f(x)=arctgx.
Предварительно разложим в ряд Маклорена функцию 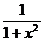 , для чего в формуле ж) заменим x на
, для чего в формуле ж) заменим x на 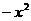 , тогда получим
, тогда получим
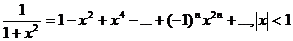 , откуда
, откуда
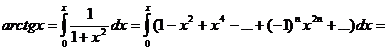
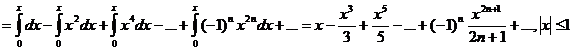 .
.
Глава XII. Обыкновенные дифференциальные уравнения
12.1 Основные понятия и определения
Определение 12.1.
Обыкновенным дифференциальным уравнением (дифференциальным уравнением) называется уравнение, содержащее независимую переменную x, неизвестную функцию y и ее производные 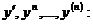
Порядком n уравнения называется порядок старшей производной, входящей в уравнение.
Определение 12.2.
Уравнение 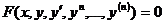 называется дифференциальным уравнением n-го порядка вобщем виде.
называется дифференциальным уравнением n-го порядка вобщем виде.
Уравнение 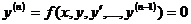 называется дифференциальным уравнением n-го порядка в нормальной форме.
называется дифференциальным уравнением n-го порядка в нормальной форме.
Определение 12.3.
Решением уравнения n-го порядка называется функция 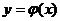 , непрерывная вместе со своими производными до порядка n включительно на некотором интервале (a;b) и обращающая данное уравнение в тождество.
, непрерывная вместе со своими производными до порядка n включительно на некотором интервале (a;b) и обращающая данное уравнение в тождество.
График решения на плоскости xОy называется интегральной кривой.
