Лекция 5. Ряды Тейлора и Маклорена
5.1. Ряды Тейлора и Маклорена. Условия сходимости
рядов Тейлора к исходной функции
Пусть функция 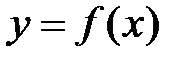 определена в некоторой окрестности точки х0:
определена в некоторой окрестности точки х0: 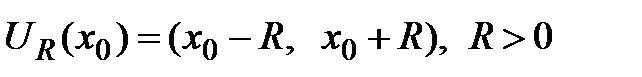 и имеет производные любого порядка,
и имеет производные любого порядка,
тогда для этой функции формально можно составить ряд по степеням 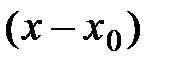 :
:
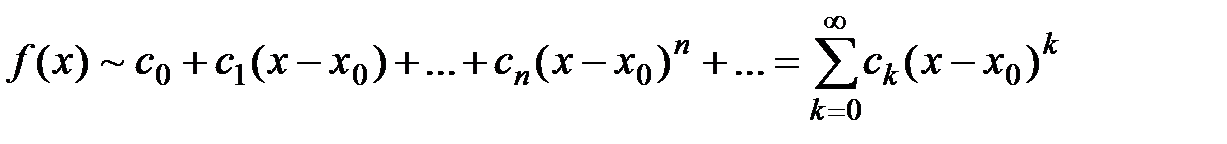 ,
,
где 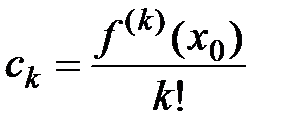 .
.
Определение 1. Обобщённый степенной ряд вида 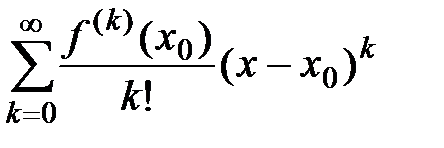
называется рядом Тейлора для функции 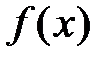 по степеням
по степеням 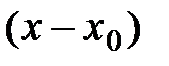 . Если положить
. Если положить  , то получим ряд
, то получим ряд 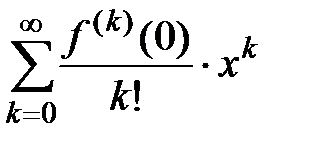 , который носит название ряда Маклорена для функции
, который носит название ряда Маклорена для функции 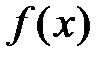 по степеням х.
по степеням х.
Задача. Пусть задана функция 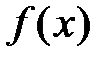 , бесконечно дифференцируемая в окрестности точки х0:
, бесконечно дифференцируемая в окрестности точки х0: 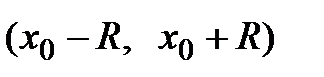 , и пусть для этой функции составлен ряд Тейлора по степеням
, и пусть для этой функции составлен ряд Тейлора по степеням 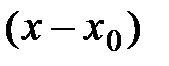 :
: 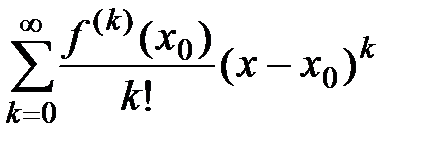 и его сумма равна
и его сумма равна 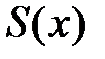 . Если интервал
. Если интервал 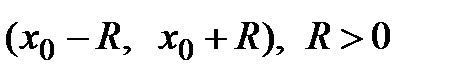 является интервалом сходимости данного ряда с радиусом сходимости R, то можно записать равенство:
является интервалом сходимости данного ряда с радиусом сходимости R, то можно записать равенство:
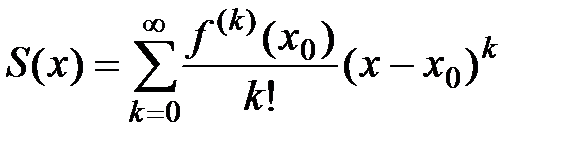
при всех 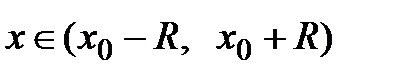 .
.
Выясним, при каких условиях такой степенной ряд имеет своей суммой функцию 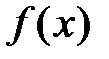 , т.е. когда
, т.е. когда 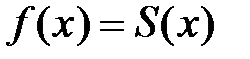 , поскольку существуют функции, для которых сумма ряда Тейлора не совпадает с данной функцией.
, поскольку существуют функции, для которых сумма ряда Тейлора не совпадает с данной функцией.
Рассмотрим пример. Дана функция 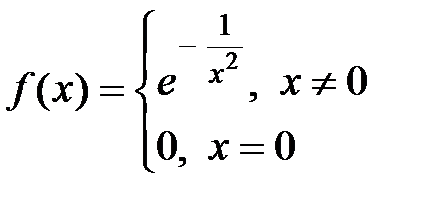 , которая является бесконечно дифференцируемой
, которая является бесконечно дифференцируемой 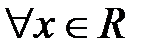 . Вычислим производные этой функции в точке
. Вычислим производные этой функции в точке  :
: 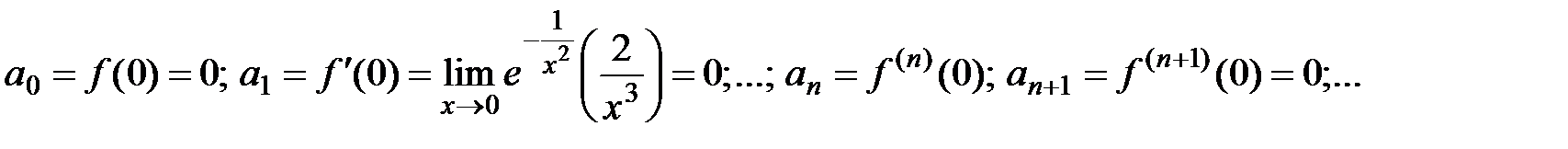 Таким образом, все вычисленные коэффициенты ряда Тейлора–Маклорена для данной функции равны 0, поэтому этот ряд сходится на всей оси, его сумма тождественно равна 0:
Таким образом, все вычисленные коэффициенты ряда Тейлора–Маклорена для данной функции равны 0, поэтому этот ряд сходится на всей оси, его сумма тождественно равна 0: 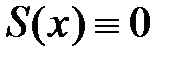 , однако
, однако 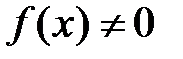 при
при 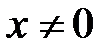 (
( 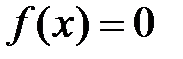 только в начале координат).
только в начале координат).
Пусть ряд Тейлора 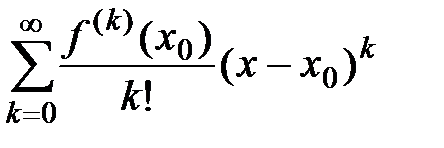 имеет интервал сходимости
имеет интервал сходимости 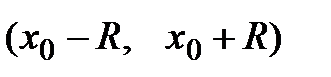 , где R – радиус сходимости. Тогда, если
, где R – радиус сходимости. Тогда, если 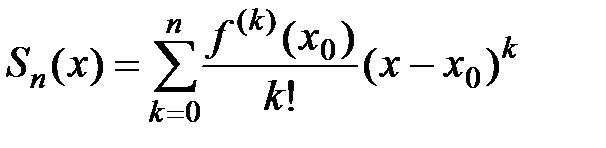 − частичная сумма этого ряда, то для любого
− частичная сумма этого ряда, то для любого 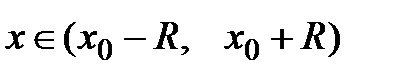 существует
существует 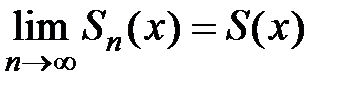 . Рассмотрим теорему, которая даёт условия того, что
. Рассмотрим теорему, которая даёт условия того, что 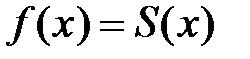 .
.
Теорема 1 (необходимый и достаточный признак сходимости ряда Тейлора к функции f(x)). Для того чтобы ряд Тейлора 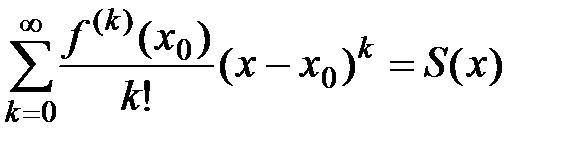 ,
, 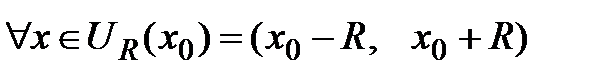 , имел своей суммой функцию
, имел своей суммой функцию 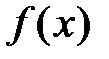 , т.е.
, т.е. 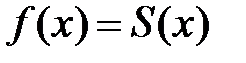 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
для всех 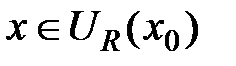 существовал предел
существовал предел 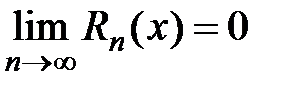 , где
, где 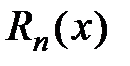 − остаток ряда Тейлора.
− остаток ряда Тейлора.
Доказательство. 1) Необходимость. Пусть функция 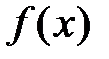 есть сумма ряда Тейлора на указанном промежутке:
есть сумма ряда Тейлора на указанном промежутке: 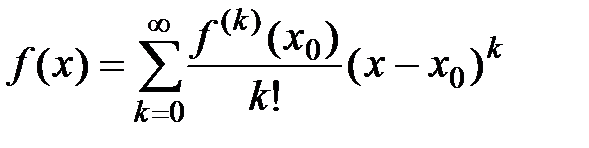 , или
, или 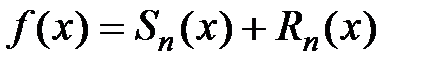 , где
, где 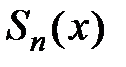 − частичная сумма ряда Тейлора,
− частичная сумма ряда Тейлора, 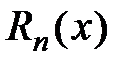 − остаток ряда Тейлора. Из условия сходимости ряда
− остаток ряда Тейлора. Из условия сходимости ряда 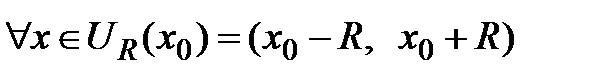 существует предел
существует предел 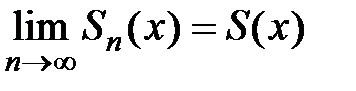 , и так как
, и так как 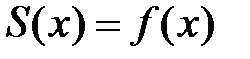 , то существует предел
, то существует предел
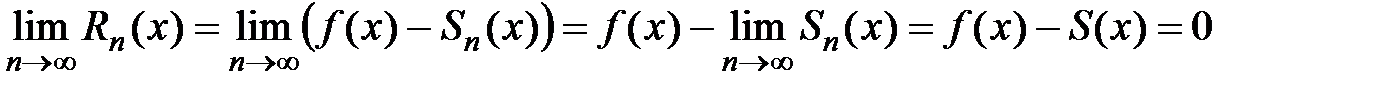 ,
,
т.е. 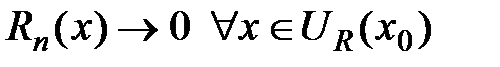 . Необходимость доказана.
. Необходимость доказана.
2) Достаточность. Пусть существует 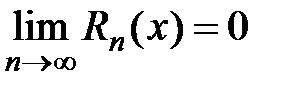 . Так как функция
. Так как функция 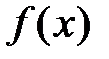 бесконечно дифференцируема при всех
бесконечно дифференцируема при всех 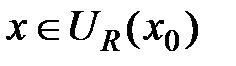 , то для неё имеет место формула Тейлора
, то для неё имеет место формула Тейлора 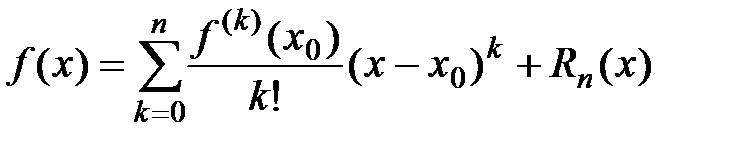 для всех
для всех 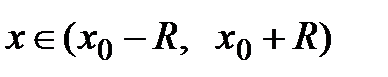 , где
, где 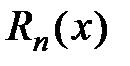 − остаточный член формулы Тейлора, который совпадает с остатком ряда Тейлора. Тогда частичная сумма соответствующего ряда Тейлора имеет вид:
− остаточный член формулы Тейлора, который совпадает с остатком ряда Тейлора. Тогда частичная сумма соответствующего ряда Тейлора имеет вид:
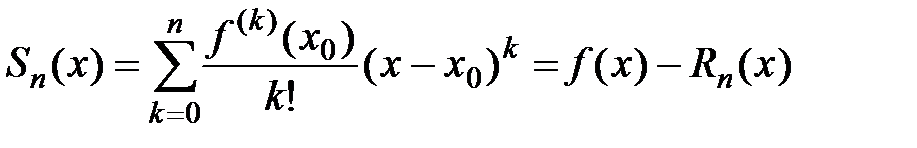 .
.
Рассмотрим предел 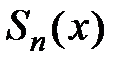 , который обозначим через
, который обозначим через 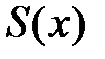 , учитывая, что
, учитывая, что 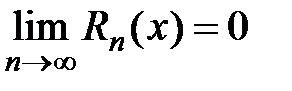 :
: 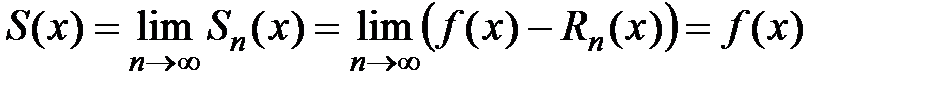 , т.е.
, т.е. 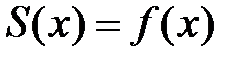 . Достаточность доказана.
. Достаточность доказана.
Замечание. Если 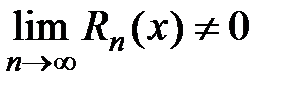 , то сумма ряда Тейлора может не совпадать
, то сумма ряда Тейлора может не совпадать
с данной функцией, т.е. 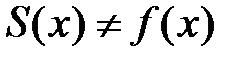 , хотя сам ряд может сходиться к другой функции.
, хотя сам ряд может сходиться к другой функции.
Необходимое и достаточное условие сходимости ряда Тейлора к
исходной функции неудобно для проверки на практике конкретных рядов; существуют более простые, хотя и более жёсткие, достаточные условия разложения функции 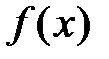 в ряды Тейлора−Маклорена. Сначала сформулируем лемму.
в ряды Тейлора−Маклорена. Сначала сформулируем лемму.
Лемма. Для любого  R существует следующий предел:
R существует следующий предел: 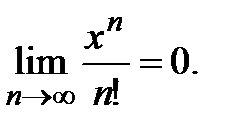
Доказательство. Рассмотрим степенной ряд 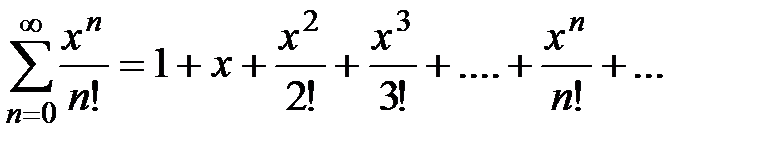 , общий член которого
, общий член которого 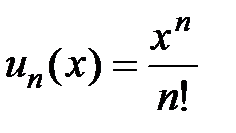 . Найдём радиус и область сходимости этого ряда, используя признак
. Найдём радиус и область сходимости этого ряда, используя признак
Даламбера. Вычисляем предел, учитывая, что 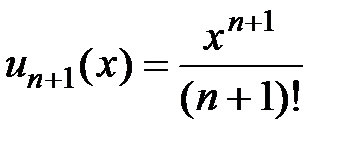 :
:
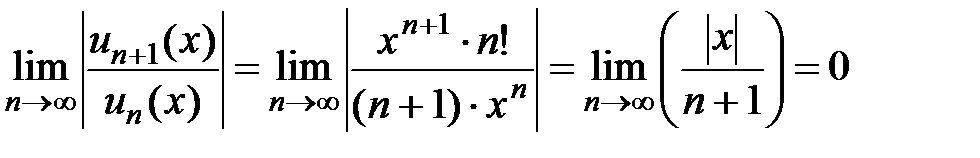 ,
,
т.е. радиус сходимости ряда 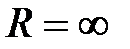 . Следовательно, рассмотренный ряд сходится для всех
. Следовательно, рассмотренный ряд сходится для всех 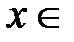 R, тогда по необходимому признаку сходимости общий член ряда
R, тогда по необходимому признаку сходимости общий член ряда 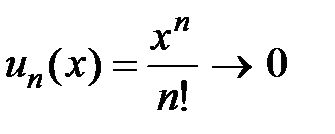 ,
, 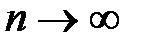 , т.е.
, т.е. 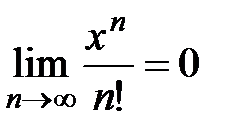 для любого
для любого
 R.
R.
Теорема 2 (достаточные условия разложимости функции f(x) в ряд Маклорена). Пусть функция  определена и бесконечно дифференцируема на интервале
определена и бесконечно дифференцируема на интервале 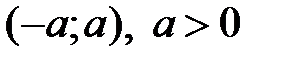 . Если существует такое число
. Если существует такое число 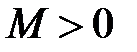 , что для каждого натурального
, что для каждого натурального 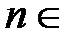 N и всех
N и всех 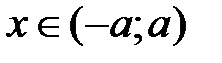 выполняется неравенство:
выполняется неравенство: 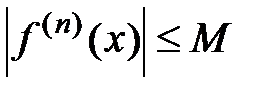 (это означает, что производные любого порядка ограничены одним и тем же числом), тогда остаток ряда Маклорена
(это означает, что производные любого порядка ограничены одним и тем же числом), тогда остаток ряда Маклорена 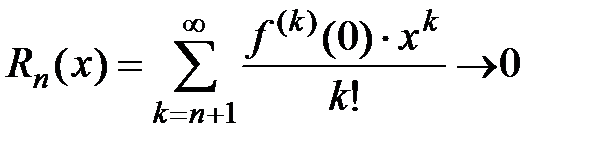 при
при 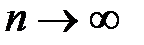 , а значит,
, а значит, 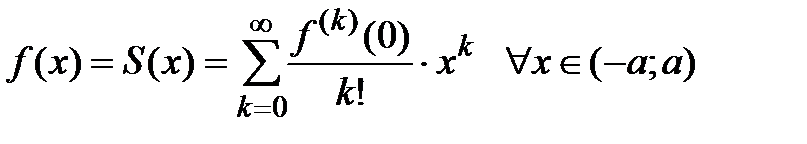 .
.
Доказательство. Покажем, что остаток ряда Маклорена стремится к нулю при 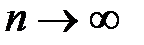 . Запишем для функции
. Запишем для функции 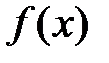 формулу Маклорена с остаточным членом в форме Лагранжа:
формулу Маклорена с остаточным членом в форме Лагранжа: 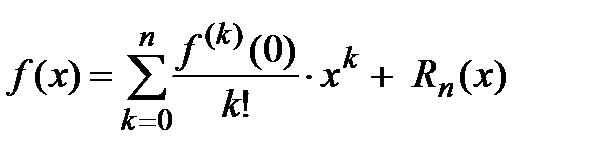 , где
, где 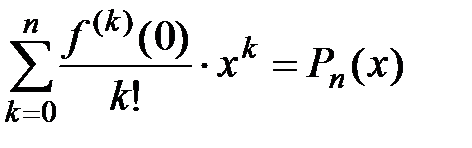 − многочлен Маклорена, а
− многочлен Маклорена, а 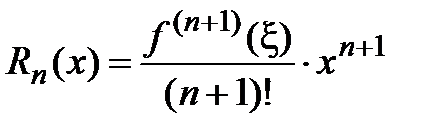 . Отметим, что частичная сумма ряда Маклорена
. Отметим, что частичная сумма ряда Маклорена 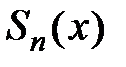 совпадает с многочленом Маклорена
совпадает с многочленом Маклорена 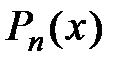 , а остаток ряда есть
, а остаток ряда есть 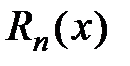 . Выполним его оценку, используя условия теоремы 2 и учитывая, что
. Выполним его оценку, используя условия теоремы 2 и учитывая, что 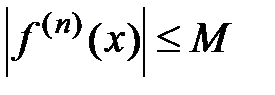 для всех
для всех 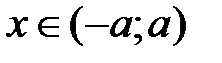 :
:
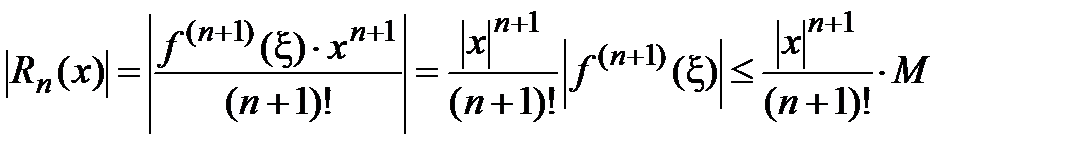 .
.
По лемме 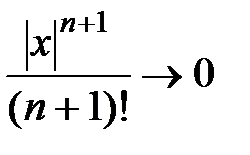 при
при 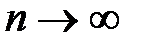 , тогда
, тогда 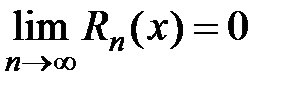 ,
, 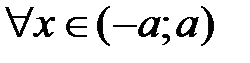 .
.
Следовательно, по теореме 1 о необходимом и достаточном признаке сходимости ряда Тейлора к исходной функции получаем 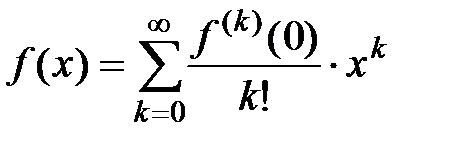 . Теорема доказана.
. Теорема доказана.
5.2. Разложение основных элементарных функций в степенные ряды
Используем изложенную выше теорию для разложения основных элементарных функций в степенные ряды. Для разложения функции 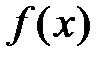
в степенной ряд по степеням 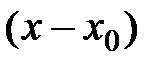 можно рекомендовать следующий
можно рекомендовать следующий
порядок действий:
1) Находим производные функции 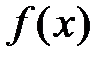 в точке
в точке 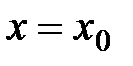 :
:
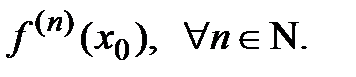
2) Составляем ряд Тейлора 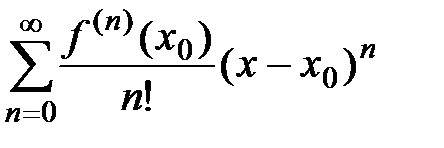 .
.
3) Находим интервал сходимости данного ряда: 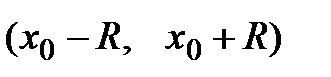 , где R– радиус сходимости.
, где R– радиус сходимости.
4) Исследуем поведение остатка ряда 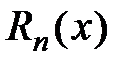 для всех
для всех
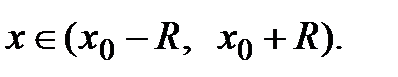
Если окажется, что 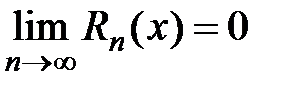 , то на основании теорем 1 и 2 делаем вывод, что
, то на основании теорем 1 и 2 делаем вывод, что 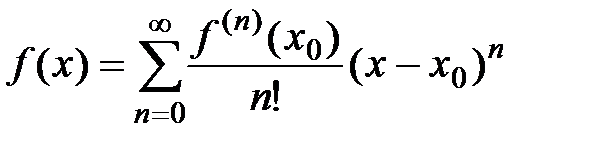 при всех
при всех 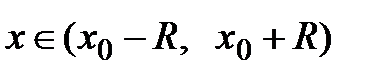 .
.
В результате получаем формулу разложения функции в степенной ряд.
· Разложение в степенной ряд функции 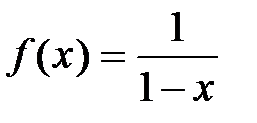 имеет вид:
имеет вид:
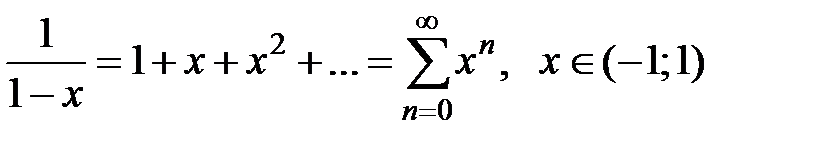 (1)
(1)
Вывод. Рассмотрим ряд геометрической прогрессии 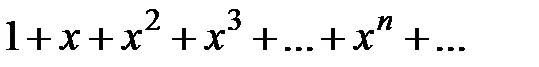 , знаменатель которой
, знаменатель которой 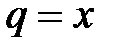 и
и 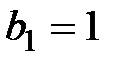 . Можно показать, что интервал сходимости этого ряда
. Можно показать, что интервал сходимости этого ряда 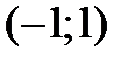 ,
, 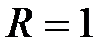 и сумма этого ряда
и сумма этого ряда 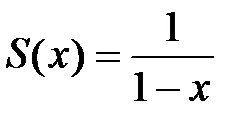 (сумма ряда бесконечно убывающей геометрической прогрессии вычисляется по формуле
(сумма ряда бесконечно убывающей геометрической прогрессии вычисляется по формуле 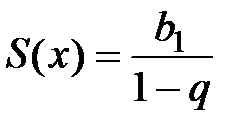 ). Оценим остаток ряда:
). Оценим остаток ряда:
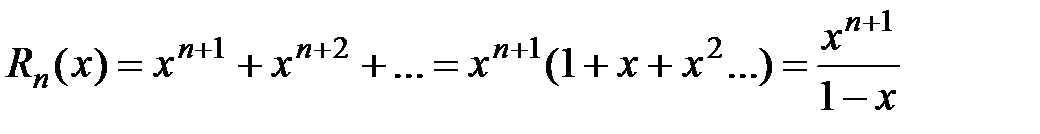 .
.
При 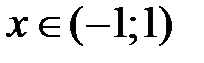
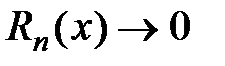 ,
, 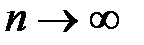 , тогда на основании теоремы 1
, тогда на основании теоремы 1
рассмотренный ряд имеет своей суммой функцию 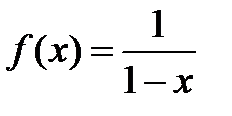 .
.
Разложение (1) имеет место.
· Разложение в степенной ряд функции 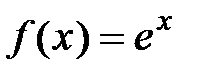 имеет вид:
имеет вид:
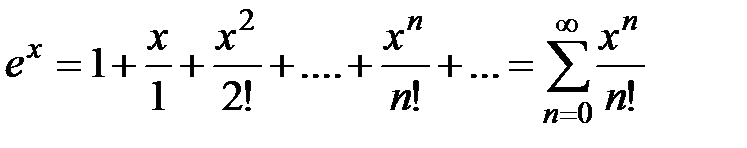 ,
, 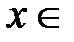 R (2)
R (2)
Вывод. Для данной функции 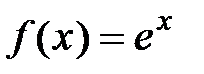 запишем ряд Маклорена:
запишем ряд Маклорена: 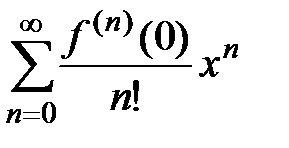 . Так как функция
. Так как функция 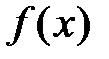 − бесконечно дифференцируема, то все производные существуют и равны
− бесконечно дифференцируема, то все производные существуют и равны 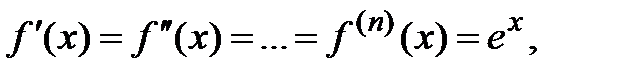
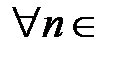 N.
N.
Находим эти производные в точке 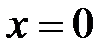 ; получаем
; получаем 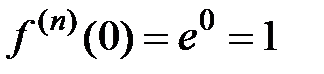 для всех
для всех 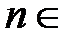 N, тогда ряд Маклорена приобретает вид:
N, тогда ряд Маклорена приобретает вид:
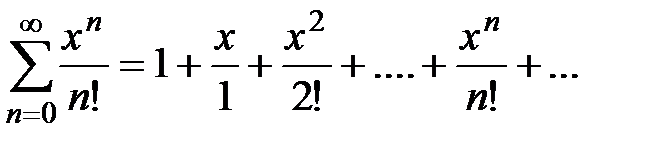 .
.
Этот ряд сходится для всех 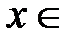 R. Покажем, что сумма этого ряда равна
R. Покажем, что сумма этого ряда равна 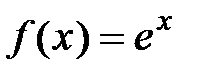 . Фиксируем некоторое число
. Фиксируем некоторое число 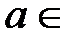 R и рассмотрим некоторый отрезок [−a; a], на котором
R и рассмотрим некоторый отрезок [−a; a], на котором 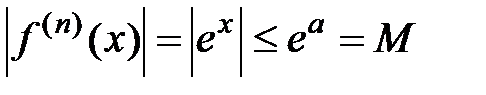 для любого
для любого  N. В этом случае по теореме 2 данный ряд Маклорена будет сходиться на указанном отрезке к исходной функции
N. В этом случае по теореме 2 данный ряд Маклорена будет сходиться на указанном отрезке к исходной функции  . Отметим, что это верно для любого фиксированного числа
. Отметим, что это верно для любого фиксированного числа  R. Разложение (2) имеет место при всех
R. Разложение (2) имеет место при всех 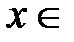 R.
R.
· Разложение в степенной ряд функции 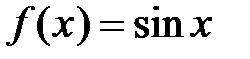 имеет вид:
имеет вид:
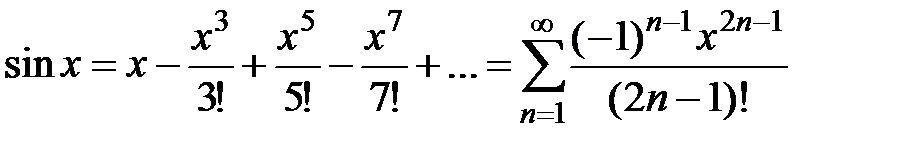 ,
, 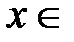 R (3)
R (3)
Вывод. Для функции 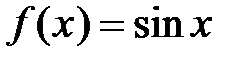 запишем ряд Маклорена
запишем ряд Маклорена 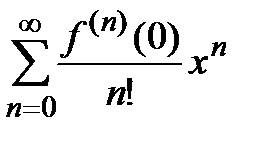 .
.
Находим все производные: 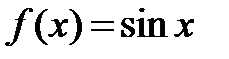 ,
, 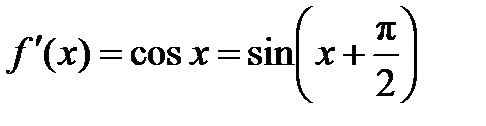 ,
, 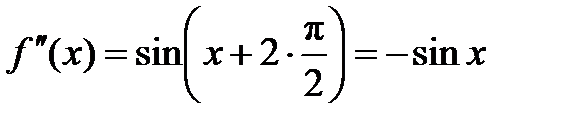 ,
, 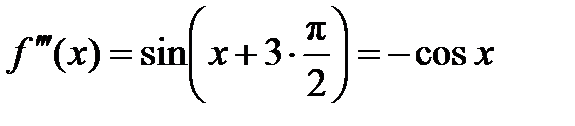 , …,
, …, 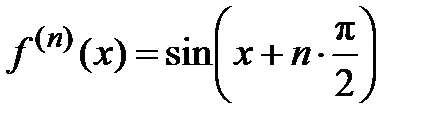 . Вычисляем эти производные в точке х = 0:
. Вычисляем эти производные в точке х = 0:
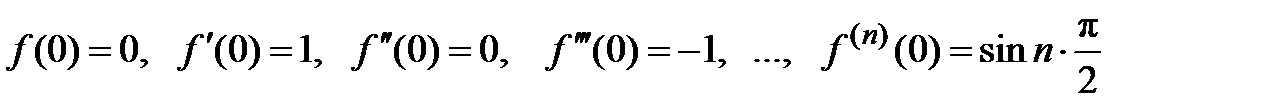 .
.
Подставив эти значения в ряд Маклорена, получаем ряд:
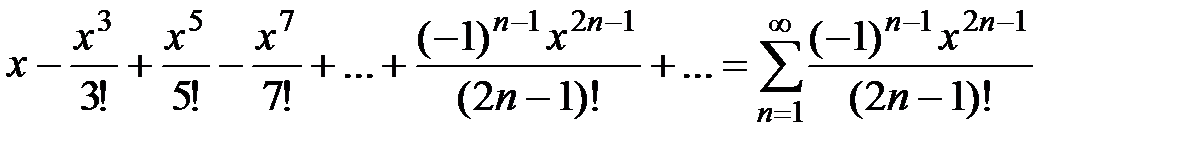 .
.
Данный ряд сходится при любом 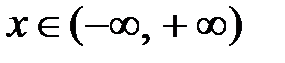 ; покажем, что он сходится к функции
; покажем, что он сходится к функции 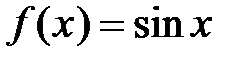 . Согласно теореме 2 (поскольку
. Согласно теореме 2 (поскольку 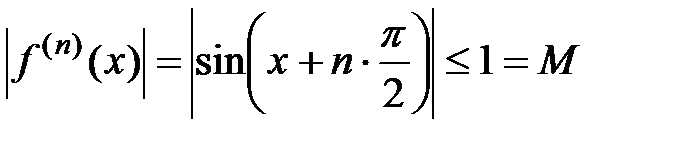 , т.е. все производные ограничены одним и тем же числом) данный ряд Маклорена будет сходиться к исходной функции
, т.е. все производные ограничены одним и тем же числом) данный ряд Маклорена будет сходиться к исходной функции 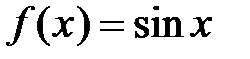 при всех
при всех  R. Таким образом разложение (3) имеет место.
R. Таким образом разложение (3) имеет место.
· Разложение в степенной ряд функции 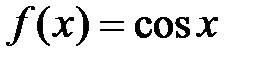 имеет вид:
имеет вид:
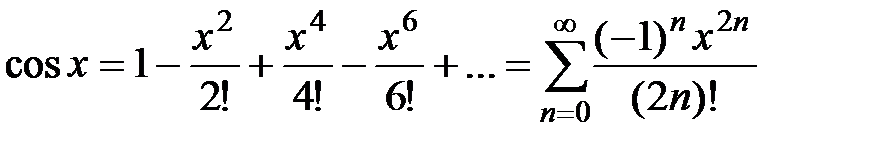 ,
, 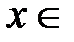 R (4)
R (4)
Вывод. Рассмотрим разложение (3)
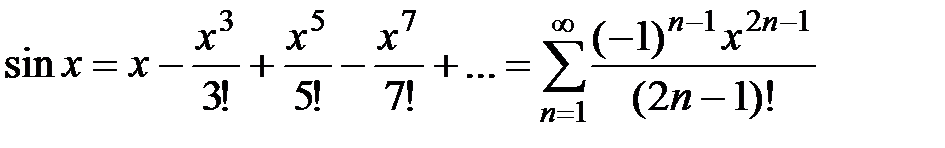 ,
, 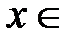 R. Продифференцируем данный степенной ряд; получившийся новый ряд будет также сходиться при всех
R. Продифференцируем данный степенной ряд; получившийся новый ряд будет также сходиться при всех 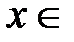 R к функции, которая равна производной от
R к функции, которая равна производной от 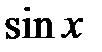 (свойство 3, лекция 4, разд. 4.3), т.е.
(свойство 3, лекция 4, разд. 4.3), т.е.
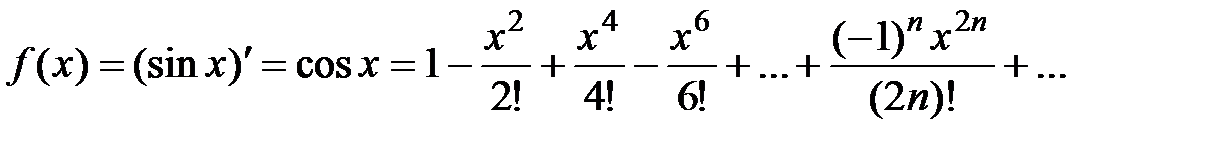 .
.
Таким образом, разложение (4) имеет место.
· Разложение в степенной ряд функции 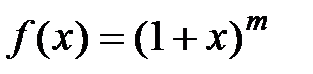 имеет вид:
имеет вид:
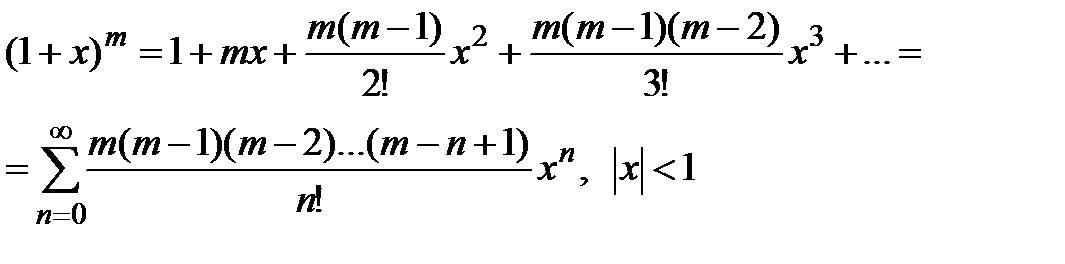 (5)
(5)
Разложение (5) приводится без вывода. Отметим, что оно верно при фиксированном 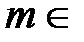 R и называется биномиальным рядом.
R и называется биномиальным рядом.
При натуральном 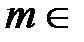 N этот ряд представляет собой конечную сумму, известную как бином Ньютона:
N этот ряд представляет собой конечную сумму, известную как бином Ньютона:
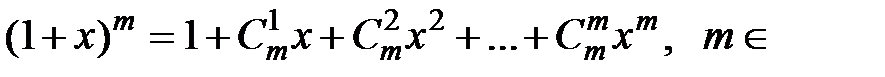 N.
N.
Для нецелых m имеет место формула Тейлора:
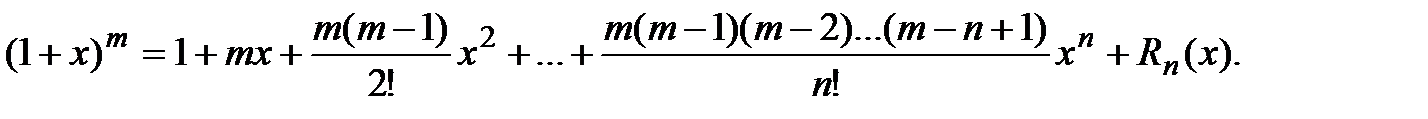
При 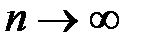 из этой формулы получаем бесконечный степенной ряд (5). Найдём радиус его сходимости, применяя признак Даламбера. Учитывая, что
из этой формулы получаем бесконечный степенной ряд (5). Найдём радиус его сходимости, применяя признак Даламбера. Учитывая, что 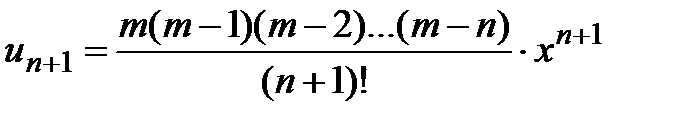 ,
, 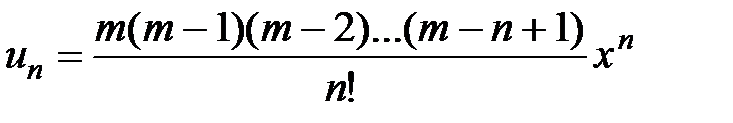 , вычисляем предел:
, вычисляем предел:
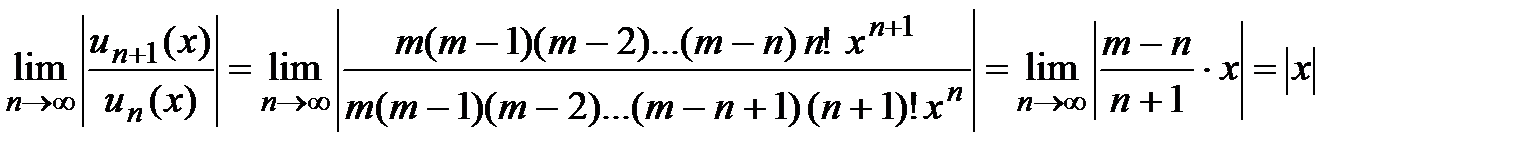 ,
,
тогда при 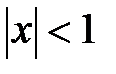 ряд сходится и его радиус сходимости
ряд сходится и его радиус сходимости 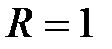 , а интервал сходимости (−1;1) ; можно показать, что
, а интервал сходимости (−1;1) ; можно показать, что 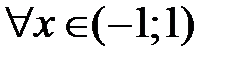 ,
, 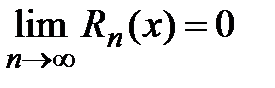 .
.
Итак, разложение (5) верно для всех 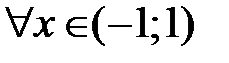 . В частном случае, когда
. В частном случае, когда 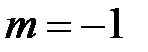 , из разложения (5) получаем ряд :
, из разложения (5) получаем ряд :
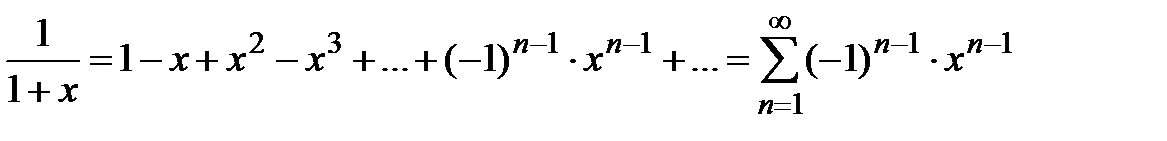 ,
,
который при 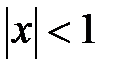 абсолютно сходится. Если в каждом члене ряда заменить х на (− х), то получим разложение (1):
абсолютно сходится. Если в каждом члене ряда заменить х на (− х), то получим разложение (1):
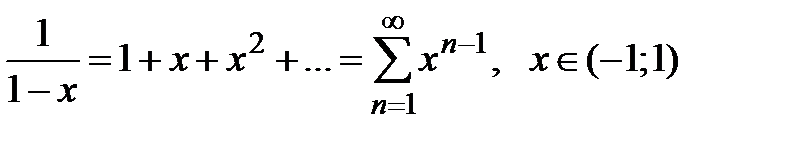 .
.
· Разложение в степенной ряд функции 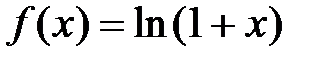 имеет вид:
имеет вид:
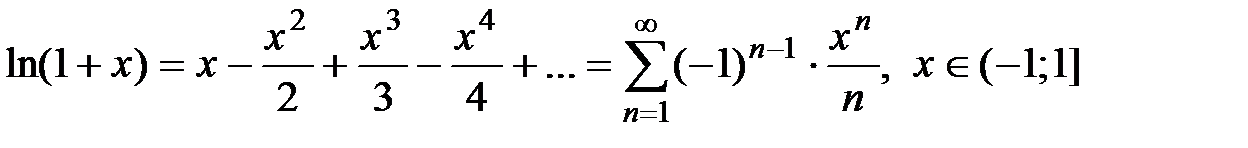 (6)
(6)
Вывод. Из разложения (5) биномиального ряда при 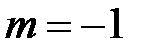 получаем ряд геометрической прогрессии со знаменателем
получаем ряд геометрической прогрессии со знаменателем 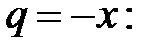
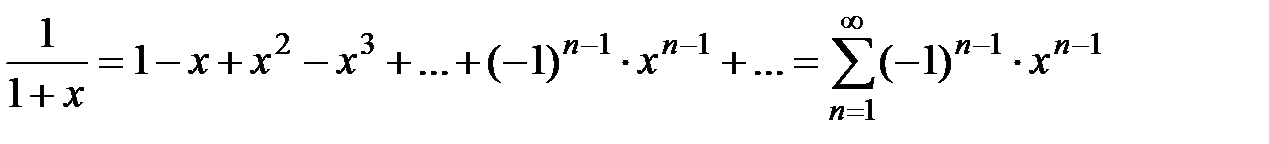 ,
,
который сходится при 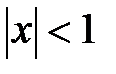 , т.е. этот ряд имеет интервал сходимости (−1;1) с радиусом сходимости
, т.е. этот ряд имеет интервал сходимости (−1;1) с радиусом сходимости 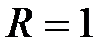 .
.
Полученный ряд почленно интегрируем на отрезке 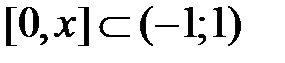 , используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:
, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:
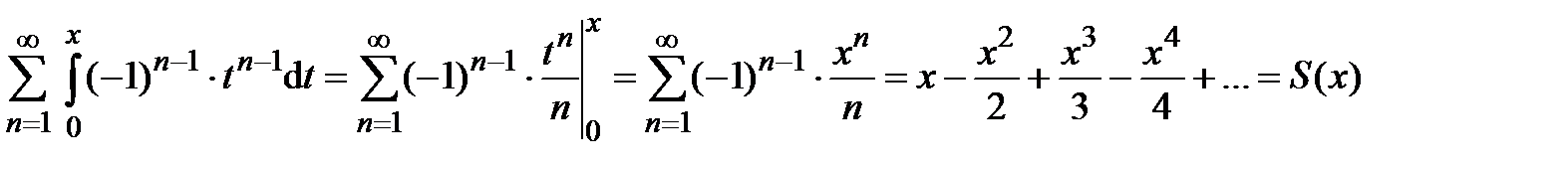 .
.
Сумма полученного ряда равна
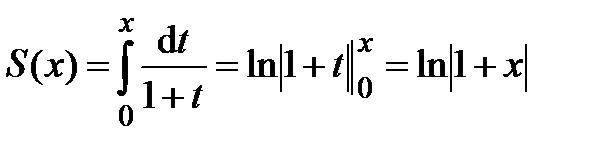
(или 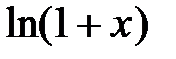 , так как
, так как 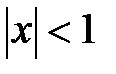 ).
).
Таким образом, 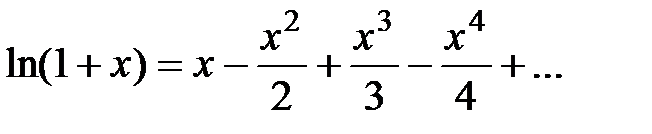 , т.е. имеет место разложение (6) при
, т.е. имеет место разложение (6) при 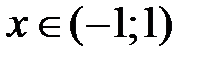 . Исследуя сходимость данного ряда в точке
. Исследуя сходимость данного ряда в точке 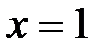 , получаем числовой ряд
, получаем числовой ряд 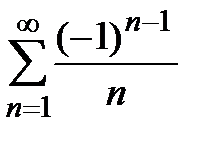 , который условно сходится. Таким образом, область сходимости ряда в разложении (6) имеет вид
, который условно сходится. Таким образом, область сходимости ряда в разложении (6) имеет вид 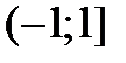 , а радиус сходимости
, а радиус сходимости 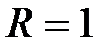 .
.
· Разложение в степенной ряд функции 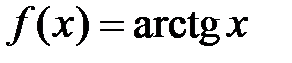 имеет вид:
имеет вид:
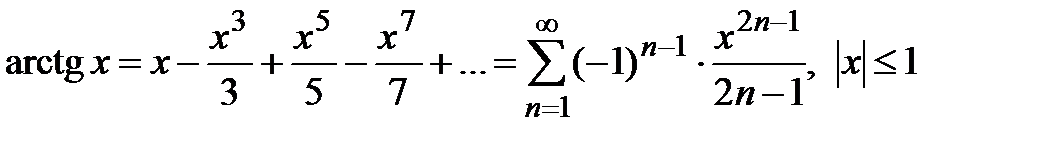 (7)
(7)
Вывод. Из разложения (5) биномиального ряда при 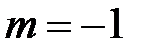 получаем
получаем
разложение
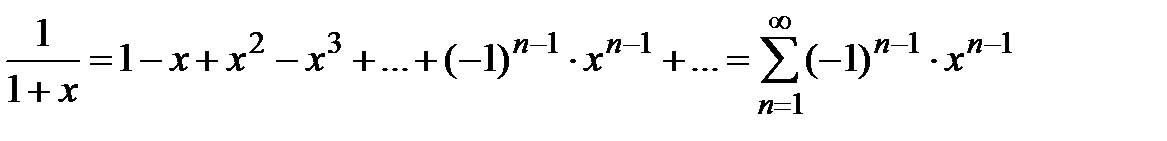 ,
,
из которого заменой  на
на 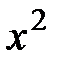 вытекает следующий ряд:
вытекает следующий ряд:
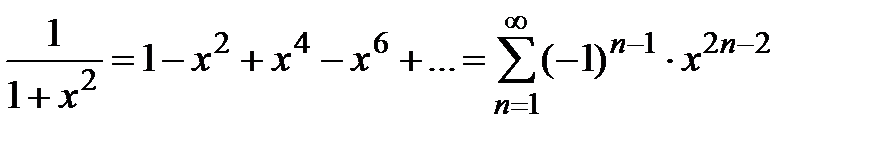 ,
,
сходящийся при 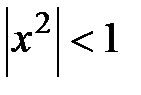 , а именно, при
, а именно, при 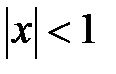 . Полученный ряд почленно интегрируем на отрезке
. Полученный ряд почленно интегрируем на отрезке 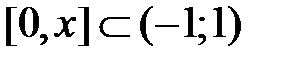 , используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится, обозначим
, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится, обозначим 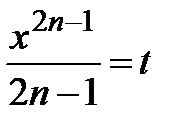 :
:
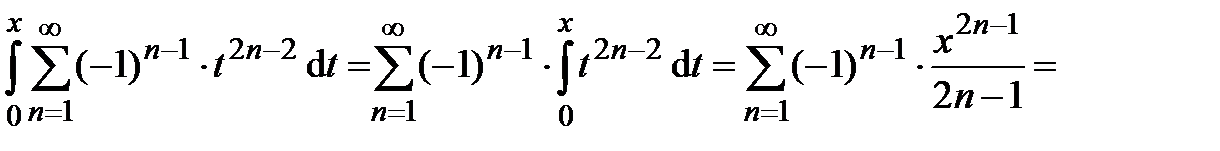
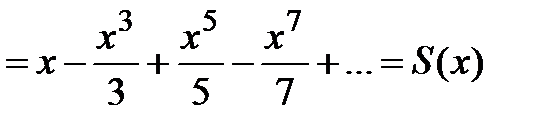 .
.
Сумма полученного ряда
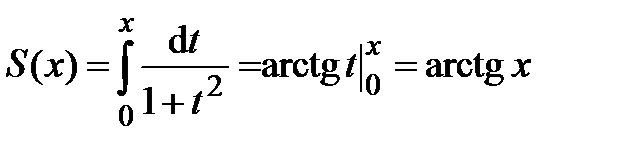 .
.
Таким образом, 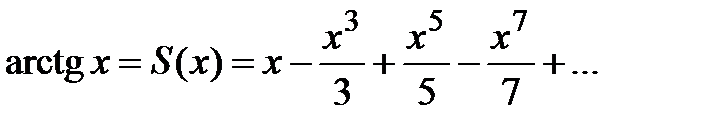 , т.е. разложение (7)
, т.е. разложение (7)
имеет место при 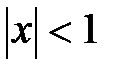 . Исследуя разложение (7) в точках
. Исследуя разложение (7) в точках 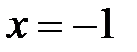 и
и 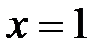 , получаем два условно сходящихся числовых ряда
, получаем два условно сходящихся числовых ряда 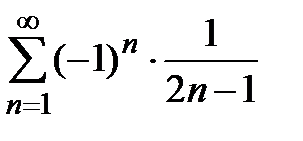 и
и 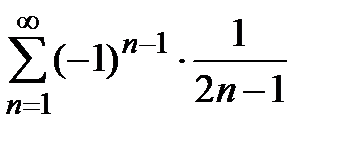 соответственно. Таким образом, область сходимости ряда (7) является отрезком
соответственно. Таким образом, область сходимости ряда (7) является отрезком 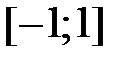 , а радиус сходимости R равен 1.
, а радиус сходимости R равен 1.
· Разложение в степенной ряд функции 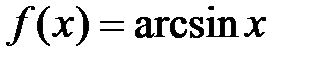 имеет вид:
имеет вид:
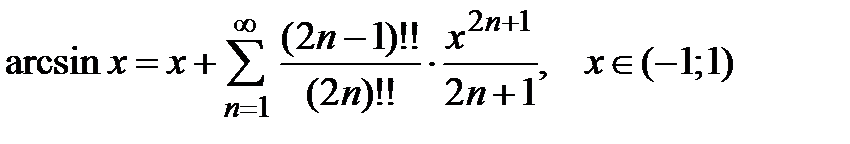 (8)
(8)
Вывод. Из разложения (5) биномиального ряда при 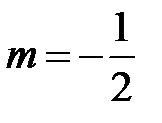 и при замене
и при замене 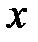 на
на 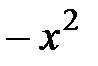 получаем разложение в степенной ряд:
получаем разложение в степенной ряд:
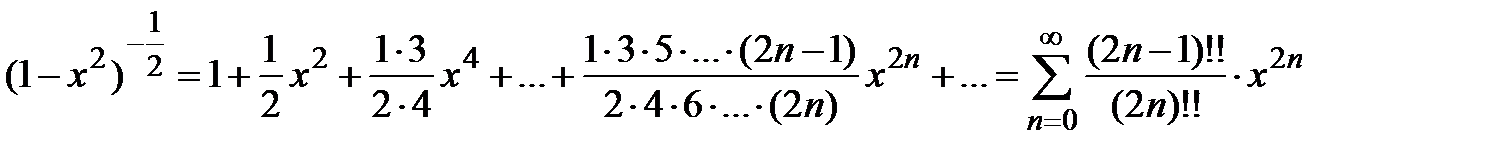 .
.
Получившийся ряд сходится при 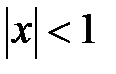 . Этот ряд почленно проинтегрируем на отрезке
. Этот ряд почленно проинтегрируем на отрезке 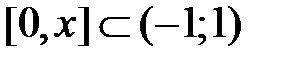 , используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:
, используя свойство 3 (лекция 4, разд. 4.3); при этом интервал сходимости сохранится:
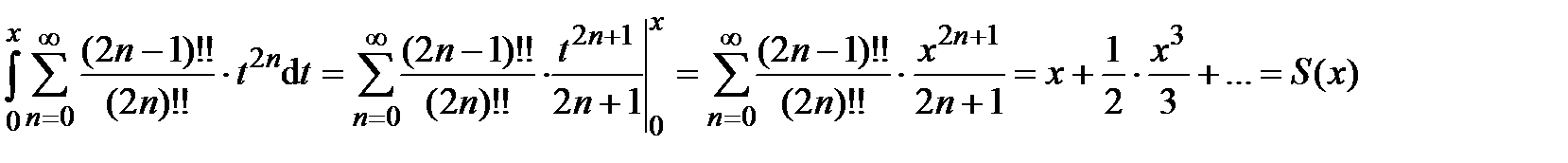 .
.
Сумма полученного ряда 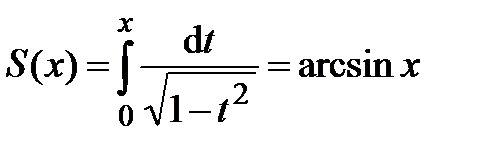 . Таким образом,
. Таким образом,
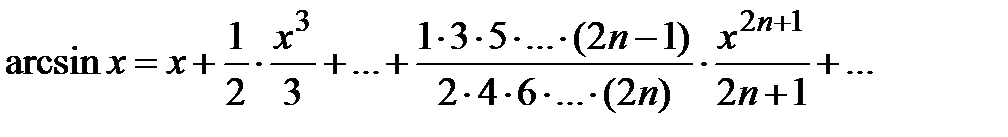 ,
,
т.е. имеет место разложение (8) на интервале сходимости 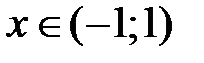 .
.
В заключение добавим, что все перечисленные в разделе 5.2 разложения называют основными разложениями элементарных функций в
степенной ряд, которые используются как эталонные для разложения
других функций.
