Основные методы вычисления определённого интеграла

1) Замена переменной в определённом интеграле.

Теорема 7.2.

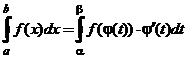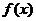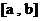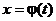Если функция непрерывна на отрезке и – функция, непрерывная вместе со своей производной 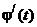на отрезке 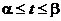, причем a≤φ(t)≤b и φ(α)=a, φ(β)=b, тогда .

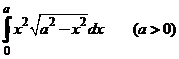Пример 7.6.

Найдем определенный интеграл заменой переменных.

Пусть 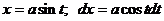, тогда и, следовательно,

, .

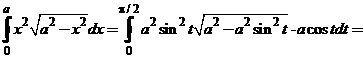
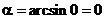Таким образом,

.

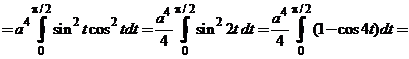
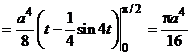Интегрирование по частям в определенном интеграле.

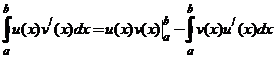Пусть функции 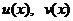– непрерывны вместе со своими производными на [a, b], тогда 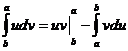или .

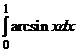Пример 7.7.

Найдем определенный интеграл: интегрированием по частям.

.

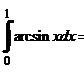
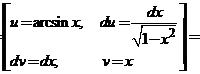
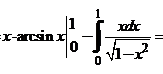
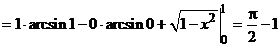Пример 7.8.

Найдем определенный интеграл: интегрированием по частям.

.

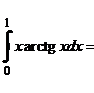
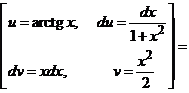
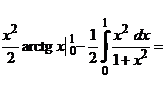
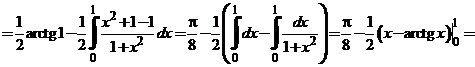
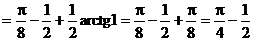Глава VIII. Геометрические приложения определенного интеграла

Вычисление площади плоской фигуры

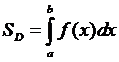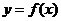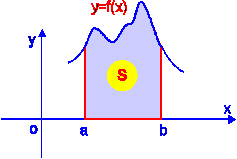
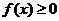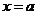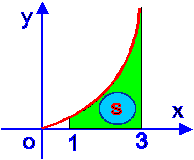
а) Если непрерывная кривая задана в прямоугольных координатах уравнением ( ), то площадь криволинейной трапеции D, ограниченной этой кривой, двумя вертикальными прямыми , 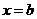и осью Ox (рис. 8.1), определяется формулой .

	рис.8.1.		рис.8.2.
		D

Пример 8.1.

Вычислим площадь плоской фигуры, ограниченной параболой 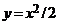, прямым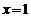и и 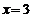и осью Ох (рис. 8.2).

Искомая площадь выражается интегралом 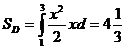(кв.ед.)

Пример 8.2.

Вычислим площадь плоской фигуры, ограниченную кривой 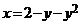и осью Oy (рис. 8.3).

y=f1(x)

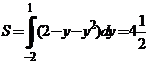Здесь изменены роли функции и аргумента (x=g(y)) и поэтому искомая площадь выражается интегралом (кв.ед.), где пределы интегрирования 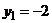, 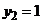найдены как ординаты точек пересечения данной кривой с осью Оу.

			рис.8.4.

y=f2(x)

y1

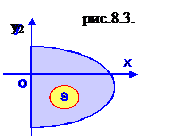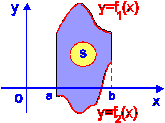
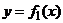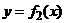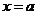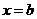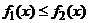б) В более общем случае, если фигура D ограничена двумя непрерывными кривыми и и двумя вертикальными прямыми , , где при 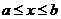(рис. 8.4), будем иметь 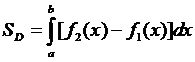. Пример 8.3.

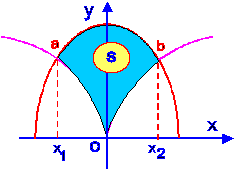
Вычислим площадь фигуры D, заключённую между кривым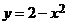и и 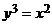(рис.8.5).

рис.8.5

рис.8.5.

Решая совместно систему уравнений 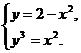, находим абсциссы точек пересечения данных кривых: 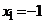и 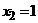. В силу формулы получим

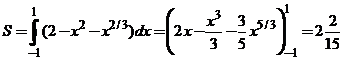(кв.ед.).

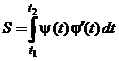в) Если кривая задана параметрическими уравнениями х = j(t), у = ψ(t), t [t₁, t₂], то площадь плоской фигуры D, ограниченной этой кривой, выражается интегралом .

Пример 8.4.

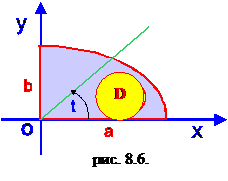
Найдем площадь, ограниченную эллипсом, используя его параметрические уравнения: x = a cos t, y = b sin t, t Î[0,2p].

Ввиду симметрии достаточно вычислить одну четверть площадь фигуры D (рис.8.6).

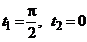Полагая в уравнении 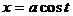сначала 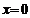, а затем 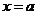, получим пределы интегрирования .

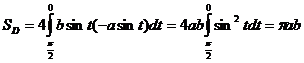(кв. ед.)

Рис. 8.6

8.2. Вычисление объёма тела вращения

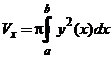а) Объём тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной кривой, заданной уравнением 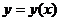, где 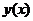–непрерывная однозначная функция на 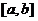, осью 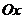и прямыми 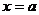, 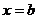вычисляется по формуле .

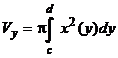б) Объём тела, образованного вращением вокруг оси Оу криволинейной трапеции, ограниченной кривой, заданной уравнением 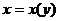, где х(у) – однозначная непрерывная функция на 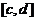, осью 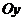и прямыми 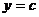, , 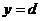вычисляется по формуле .

Пример 8.5.

у

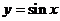
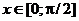Вычислим объём тела, полученного вращением фигуры, ограниченной линиями , и осью 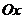вокруг оси (рис.8.7).

х

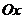	рис.8.7.

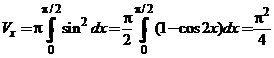Имеем (куб.ед.).

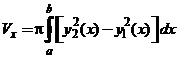
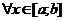
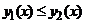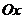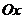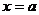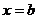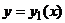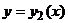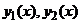б)В более общем случае объём тела, образованного вращением вокруг оси фигуры, ограниченной осью и линиями , , , , где – непрерывные неотрицательные функции ( ), равен .

Пример 8.6.

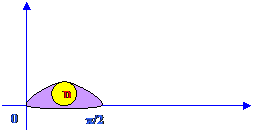
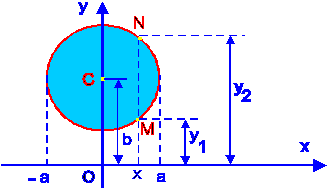
Найдем объём тора, образованного вращением круга 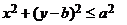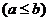вокруг оси (рис. 8.8).

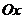рис.8.8.

Имеем 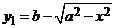и .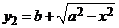

Таким образом, =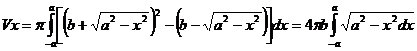

=2 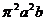(куб.ед.)

Последний интеграл берётся подстановкой: 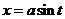.