Возрастание и убывание функции

Теорема 4.6. (о необходимом условии монотонности функции).

Если дифференцируемая на промежутке Х функция f(x) возрастает (убывает) на этом промежутке, то f′(x) ≥ 0 (f′(x) ≤ 0) при всех х Х.

Теорема 4.7. (о достаточном условии монотонности функции).

Если функция f(x) дифференцируема на промежутке Х и f′(x) > 0 (f′(x) < 0)

при всех х Х, кроме возможно конечного числа точек, где f′(x) = 0, то эта функция возрастает (убывает) на Х.

Пример 4.5.

Найдем интервалы постоянной монотонности функции f(x) = е^х – х.

Вычислив производную f′(x) = е^х – 1, получим, что f′(x) > 0 при х > 0 и f′(x)<0, и только в единственной точке х = 0 f′(x) = 0. По теореме 4.7 функция f(x) = е^х – х возрастает на (0, +∞) и убывает на (- ∞, 0).

Экстремумы функции

Определение 4.1.

Пусть функция f(x) определена на промежутке Х.

1. Точка х₀ Х называется точкой минимума (точкой максимума) функции f(x), если в некоторой окрестности О_δ(х₀) 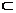Х точки х₀ выполняется неравенство f(x) > f(x₀) (f(x) < f(x₀)) при всех х О_δ(х₀), х ≠ х₀.

2. Значение функции f(x₀) называется минимумом (максимумом) функции f(x).

3. Минимум или максимум функции называется экстремумом этой функции, а точка, в которой это значение принимается, называется точкой экстремума функции.

Экстремум является локальной характеристикой функции f(x), поскольку представляет ее поведение лишь в окрестности точки х₀.

Рассмотрим график некоторой функции у = f(x) (рис. 4.3).

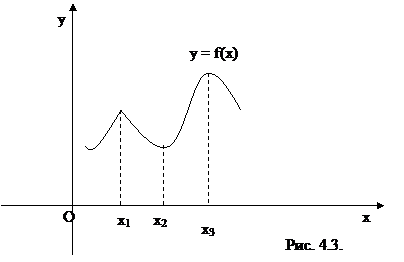Для данной функции точки х₁ и х₃ есть точки максимума, а точка х₂ – точка минимума.

Теорема 4.8. (о необходимом условии экстремума)

Если функция f(x) дифференцируема в точке экстремума х_0, то f'(x₀) = 0.

Следствие

Если точка х₀ является точкой экстремума функции f(x), то либо f'(x₀) = 0, либо f'(x₀) не существует.

Точки, в которых производная равна нулю или не существует, называются точками, подозрительными на экстремум.

Теорема 4.9 (о достаточном условии экстремума).

Пусть функция f(x) дифференцируема в некоторой окрестности точки x₀ за исключением возможно самой точки x₀, а в самой точке x₀ функция f(x) непрерывна, тогда:

1) если при переходе через точку x₀ производная f'(x) меняет знак с «-» на «+», то точка x₀ является точкой минимума функции f(x);

2) если при переходе через точку x₀ производная f'(x) меняет знак с «+» на

«-», то точка x₀ является точкой максимума функции f(x);

Пример 4.6.

Функция f(x)= 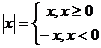не имеет производной в точке х₀ (см. пример 3.3).

Тем не менее, при переходе через эту точку производная меняет знак с « - » на «+», следовательно, точка х₀ = 0 является точкой минимума данной функции (рис.4.4).

		Рис. 4.4.

Пример 4.7.

Найдем точки экстремума функции f(x) = 2х + 3 .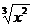

Определим точки, подозрительные на экстремум, для чего вычислим производную f'(x) = 2 + .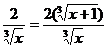

Производная f'(x) обращается в нуль в точке х₁ = -1 и не существует в точке х₂ = 0. Следовательно, исходная функция имеет две точки, подозрительные на экстремум: х₁ = -1, х₂ = 0.

Составим следующую таблицу:

x	(-∞,-1)	-1	(-1,0)		(0,+∞)
Знак f''(x)	+		-	не существует	+

Как видно из таблицы, производная f'(x) меняет знак при переходе через точки х₁ = -1 и х₂ = 0. Согласно теореме 4.9 точка х₁ = -1 является точкой максимума, а точка х₂ = 0 есть точка минимума.

y

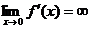Из равенства f'(-1) = 0 следует, что касательная к графику функции в точке М(-1;1) параллельна оси Ох, а поскольку , то в точке О(0;0) график функции имеет вертикальную касательную (рис.4.5).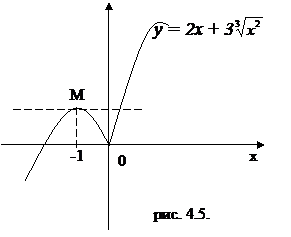