Исследование функции на возрастание и убывание
Теорема. 1) Если функция  имеет производную на отрезке
имеет производную на отрезке 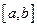 и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е.
и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. 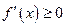 .
.
2) Если функция  непрерывна на отрезке
непрерывна на отрезке 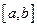 и дифференцируема на промежутке
и дифференцируема на промежутке 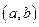 , причем
, причем 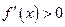 для
для 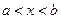 , то эта функция возрастает на отрезке
, то эта функция возрастает на отрезке 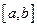 .
.
Доказательство. 1) Если функция  возрастает, то
возрастает, то 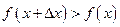 при
при 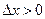 и
и 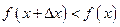 при
при 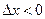 . Тогда:
. Тогда:
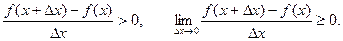
2) Пусть 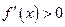 для любых точек
для любых точек 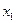 и
и 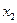 , принадлежащих отрезку
, принадлежащих отрезку 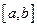 , причем
, причем 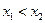 . Тогда по теореме Лагранжа находим
. Тогда по теореме Лагранжа находим 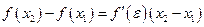 ,
, 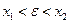 .
.
По условию 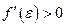 , следовательно,
, следовательно, 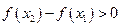 , т.е. функция
, т.е. функция  возрастает.
возрастает.
Теорема доказана.
Аналогично можно доказать, что если функция  убывает на отрезке
убывает на отрезке 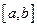 , то
, то 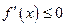 на этом отрезке. Если
на этом отрезке. Если 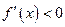 в промежутке
в промежутке 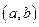 , то
, то  убывает на отрезке
убывает на отрезке 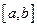 .
.
Конечно, данное утверждение справедливо, если функция  непрерывна на отрезке
непрерывна на отрезке 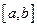 и дифференцируема на интервале
и дифференцируема на интервале 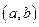 .
.
Определение. Функция  имеет в точке
имеет в точке 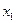 максимум, если ее значение в этой точке больше значений во всех точках некоторой окрестности, содержащей точку
максимум, если ее значение в этой точке больше значений во всех точках некоторой окрестности, содержащей точку 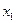 . Функция
. Функция  имеет в точке
имеет в точке 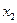 минимум, если
минимум, если 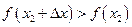 при любом
при любом 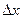 (
( 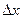 может быть и отрицательным).
может быть и отрицательным).
Оределение. Точки максимума и минимума функции называются точками экстремума.
Теорема. (необходимое условие существования экстремума) Если функция  дифференцируема в точке
дифференцируема в точке 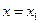 и точка
и точка 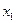 является точкой экстремума функции, то производная функции
является точкой экстремума функции, то производная функции  обращается в нуль в этой точке.
обращается в нуль в этой точке.
Доказательство. Предположим, что функция  имеет в точке
имеет в точке 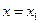 максимум (для минимума доказательство аналогично). Тогда при достаточно малых положительных
максимум (для минимума доказательство аналогично). Тогда при достаточно малых положительных 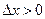 верно неравенство:
верно неравенство:
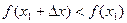 , т.е.
, т.е. 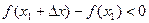 .
.
Тогда
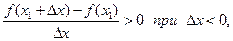
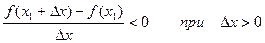 .
.
По определению:
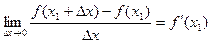 ,
,
т.е. если 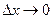 , но
, но 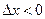 , то
, то 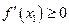 , а если
, а если 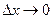 , но
, но 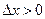 , то
, то 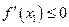 .
.
А это возможно только в том случае, если при 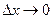
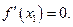 Теорема доказана.
Теорема доказана.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то отсюда вообще говоря не следует, что в этой точке функция имеет экстремум. Например, функция 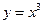 имеет производную в точке
имеет производную в точке 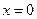 равную нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
равную нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но не достаточные. Например, 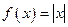 и
и 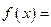
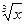 .
.
Вообще говоря, функция  может иметь экстремум в точках, где производная не существует или равна нулю.
может иметь экстремум в точках, где производная не существует или равна нулю.
Теорема. (Достаточные условия существования экстремума) Пусть функция  определена и непрерывна в интервале
определена и непрерывна в интервале 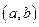 , содержащим критическую точку
, содержащим критическую точку 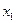 , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки
, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки 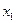 ).
).
Если при переходе через точку 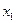 слева направо производная функции
слева направо производная функции 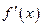 меняет знак с “+” на “-“, то в точке
меняет знак с “+” на “-“, то в точке 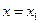 функция
функция  имеет максимум, а если производная меняет знак с “-“ на “+”- то функция
имеет максимум, а если производная меняет знак с “-“ на “+”- то функция  имеет в точке
имеет в точке 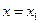 минимум.
минимум.
Доказательство. Пусть 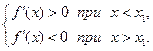 По теореме Лагранжа:
По теореме Лагранжа: 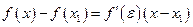 , где
, где 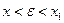 .
.
Тогда: 1) Если 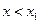 , то
, то 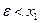 ;
; 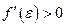 ;
; 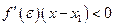 . Следовательно
. Следовательно
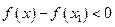 или
или 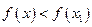 .
.
2) Если 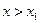 , то
, то 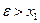 ;
; 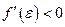 ;
; 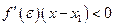 . Следовательно
. Следовательно
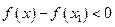 или
или 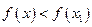 .
.
Так как ответы совпадают, то 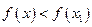 в любых точках в некоторой окрестности точки
в любых точках в некоторой окрестности точки 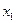 , т.е.
, т.е. 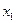 – точка максимума. Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.
– точка максимума. Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.
На основе вышесказанного можно сформулировать алгоритм для нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции.
2) Найти значения функции в критических точках.
3) Найти значения функции на концах отрезка.
4) Выбрать среди полученных значений наибольшее и наименьшее.
