Возрастание и убывание функции.

Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если

f(x₂) > f(x₁) при x₂ > x₁.

Из этого определения следует, что у возрастающей в интервале (a,b) функции f(x) в любой точке этого интервала приращения Dx и Dy имеют одинаковые знаки.

Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если

f(x₂) < f(x₁) при x₂ > x₁.

Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения Dx и Dy имеют разные знаки.

Экстремумы Функции.

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ¢(x_о) = 0, либо f ¢(x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ¢ (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную
f ¢ (x) в окрестности точки x_о и вторую производную 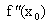в самой точке x_о. Если f ¢(x_о) = 0, 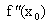>0 ( <0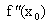), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же 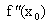=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Точки перегиба.

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.

Вертикальная

Вертикальная асимптота — прямая вида 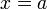при условии существования предела .

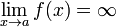Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1.

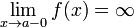
2.

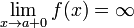
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида 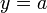при условии существования предела

.

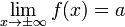Наклонная

Наклонная асимптота — прямая вида 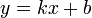при условии существования пределов

1.

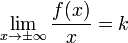
2.

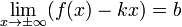
35)Схема исследования функции.

1. Область определения

2. Исследование функции на четность, нечетность и периодичность

Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенств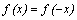о , то 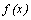– четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенств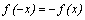о , то 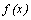– нечетная функция; в противном случае, 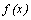– общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

3. Нахождение точек пересечения графика функции с осями координат

Точки пересечения с осью ОХ: 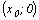, где 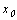– решение уравнения .

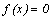Точки пересечения с осью ОY: .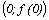

4. Нахождение промежутков знакопостоянства функции

Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е. 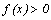или .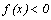

5. Нахождение производной функции, области определения производной, критических точек

Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.

6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов

Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.

7. Нахождение промежутков выпуклости функции и точек перегиба

Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.

8. Исследование поведения функции на бесконечности и в окрестности точек разрыва

Для исследования поведения функции в окрестности точки разрыва 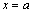необходимо вычислить односторонние пределы: 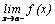и 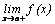. Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая 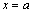– вертикальная асимптота.

При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот пр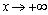и и 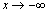. Для этого нужно вычислить следующие пределы: 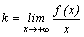и 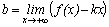. Если оба предела существуют, то 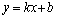– уравнение наклонной асимптоты при 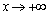. Частный случай наклонной асимптоты при 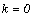– горизонтальная асимптота. Аналогично ищется наклонная асимптота при .

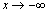9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках).