Глава III. Производная и дифференциал функции одной переменной

Производная функции в точке. Односторонние производные

Определение 3.1.

Пусть функция f(x) определена в некоторой окрестности точки х₀. Если существует конечный предел 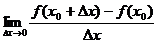, то он называется производной функции f(x) в точке х₀.

Обозначение: f'(x₀)= .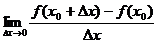

(Другие обозначения: у'(х₀), ).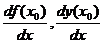

Выражение 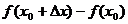называется приращением функции f(x) в точке х₀ и обозначается Δу. Таким образом, f'(x₀)= .

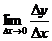Замечание 3.1.

Отметим, что производная f'(x₀) есть число. Если же производная функции f(x) существует для всех точек некоторого промежутка Х, то сопоставив каждой точке х₀ Х значение f'(x₀), получим функцию, которая называется производной функции f'(x) и обозначается f'(x) или у'.

Пример 3.1.

Найдем по определению производную функции f(x) = sin x. Пусть х₀ – произвольное вещественное число.

.

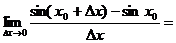
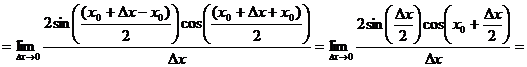
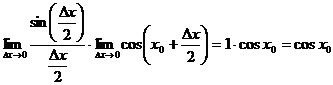Таким образом, sin'(x₀) = cos x₀. В силу произвольного выбора числа х₀ имеем (sinx)' = cos x для всех х /R.

Пример 3.2. (механический смысл производной).

Пусть прямолинейное движение материальной точки описывается уравнением s = s(t), где s(t)- функция перемещения.

Для нахождения скорости движения точки в момент времени t₀ найдем среднюю скорость точки на промежутке времени от t₀ до t₀+Δt: ν_ср. =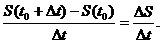

В случае неравномерного движения, чем меньше Δt, тем точнее средняя скорость характеризует скорость ν(t₀) в момент времени t_0. Поэтому скорость ν(t₀) логично считать равной пределу, к которому стремится средняя скорость, когда Δt→0, то есть ν(t₀) = .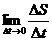

Следовательно, если в точке t₀ существует производная s'(t₀), то ν(t₀)= s'(t₀).

Таким образом, скорость прямолинейно движущейся точки равна производной функции перемещения по времени.

Определение 3.2.

Если функция f(x) определена в левой полуокрестности точки х₀ и существует конечный предел 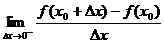, то этот предел называется левой производной функции f(x) в точке х₀.

Обозначение: f_{_}'(x₀)= .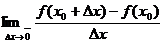

Аналогично определяется правая производная функции f(x) в точке х₀.

Обозначение: f₊'(x₀)= .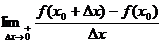

Теорема 3.1. (о равенстве односторонних производных).

Пусть функция f(x) определена в некоторой окрестности точки х_0. Для того, чтобы функция f(x) имела в точке х₀ производную f'(x₀) необходимо и достаточно существования и равенства в этой точке левой и правой производных, при этом f_{_}'(x₀) = f₊'(x₀)= f'(x₀).

Пример 3.3.

Рассмотрим функцию f(x) = 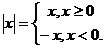Найдем односторонние производные этой функции в точке х₀ = 0:

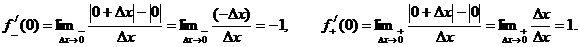
Поскольку f_{_}'(0)≠ f₊'(0), то по теореме 3.1 у функции f(x)= 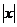не существует производной в точке (x₀)=0.

Определение 3.3.

1. Функция f(x) называется дифференцируемой в точке х₀, если в этой точке существует производная f'(x₀).

2. Функция f(x) называется дифференцируемой на интервале (a, b), если она дифференцируема в каждой точке этого интервала.

3. Функция f(x) называется дифференцируемой на отрезке [a, b], если она дифференцируема на интервале (a, b) и в точках a, b имеет односторонние производные f₊'(a) и f_{_}'(b) соответственно.

Теорема 3.2. (о связи непрерывности и дифференцируемости функции).

Если функция f(x) дифференцируема в точке х₀ , то она непрерывна в этой точке. Обратное, вообще говоря, невидно. Например, легко показать, что функция f(x)= 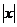непрерывна в точке х₀=0 (см. также рис.1.5.), однако в этой точке данная функция не является дифференцируемой.