Производная и дифференциал функции
1. Понятие производной. Пусть функция 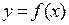 определена в некоторой окрестности точки x.
определена в некоторой окрестности точки x.
Производной функции 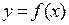 в точке x называется предел отношения приращения функции к приращению аргумента Δx при
в точке x называется предел отношения приращения функции к приращению аргумента Δx при 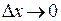 , если таковой существует:
, если таковой существует:
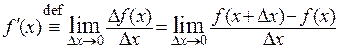 (1)
(1)
Другое обозначение производной: 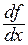 . В физике часто производную по времени обозначают точкой над значком функции:
. В физике часто производную по времени обозначают точкой над значком функции: 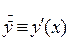 .
.
Вводят также понятия односторонних производных, то есть правых (левых) производных, если предел в формуле (1) понимать как правый (левый) предел. Обозначаются правые - левые производные 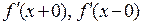 соответственно. Например,
соответственно. Например,
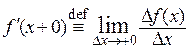
Для того, чтобы существовала производная в точке x , необходимо и достаточно, чтобы существовали равные между собой правая и левая производные, при этом
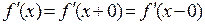 .
.
С точки зрения физики, производная от координаты пути 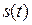 по времени при прямолинейном равномерном движении материальной точки есть мгновенная скорость,
по времени при прямолинейном равномерном движении материальной точки есть мгновенная скорость, 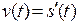 . По аналогии с кинематической скоростью говорят, что производная от любой функции – это скорость изменения функции по данному аргументу.
. По аналогии с кинематической скоростью говорят, что производная от любой функции – это скорость изменения функции по данному аргументу.
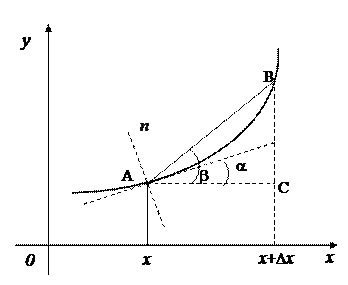
С точки зрения геометрии, производная функции равна тангенсу угла наклона касательной к графику функции 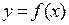 в данной точке x или угловому коэффициенту k касательной:
в данной точке x или угловому коэффициенту k касательной:
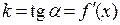 .
.
И тогда уравнение касательной в точке x0 к графику функции 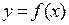 запишется:
запишется:
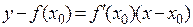
Нормалью к кривой 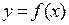 в данной точке x0 называется прямая, перпендикулярная к касательной в этой точке. Так как угол наклона нормали отличается на π/2 от угла наклона касательной α, то угловой коэффициент нормали равен
в данной точке x0 называется прямая, перпендикулярная к касательной в этой точке. Так как угол наклона нормали отличается на π/2 от угла наклона касательной α, то угловой коэффициент нормали равен 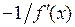 и уравнение нормали имеет вид
и уравнение нормали имеет вид
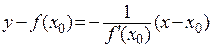
2. Правила вычисления производных.Пусть функции 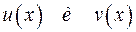 имеют производняе в точке х. Тогда
имеют производняе в точке х. Тогда
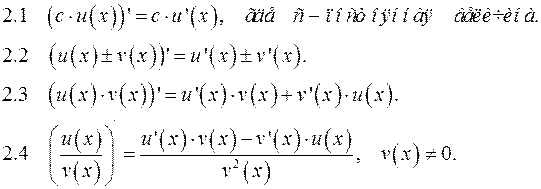
2.5 Пусть функции 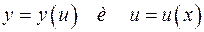 имеют производные соответственно в точках
имеют производные соответственно в точках 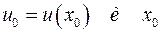 . Тогда
. Тогда 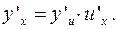
2.6 Производная функции 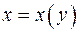 , если задана функция
, если задана функция 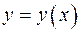 , имеет вид
, имеет вид 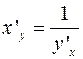 .
.
2.7 Производная функции, заданной параметрически 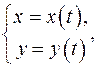 имеет вид
имеет вид 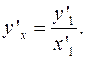
2.8 Производная функции 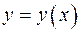 , заданной неявно уравнением
, заданной неявно уравнением 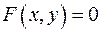 , имеет вид
, имеет вид 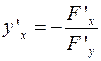 .
.
Таблица производных
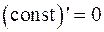 | 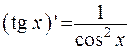 | ||
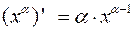 | 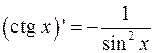 | ||
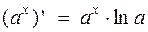 | 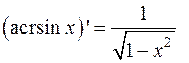 | ||
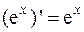 | 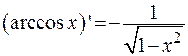 | ||
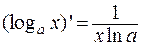 | 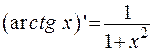 | ||
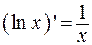 | 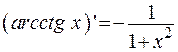 | ||
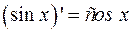 | 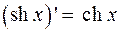 | ||
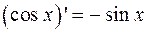 | 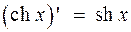 |
4. Понятие дифференциала.Функция 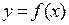 называется дифференцируемой в точке x, если ее приращение в точке x записывается в виде
называется дифференцируемой в точке x, если ее приращение в точке x записывается в виде
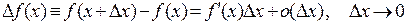 (1)
(1)
Для того, чтобы функция была дифференцируемой в точке x необходимо и достаточно, чтобы существовала производная в этой точке. Потому функции имеющие производную называют дифференцируемыми, а операцию вычисления производной называют дифференцированием.
Главную линейную часть 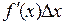 приращения функции называют дифференциалом функции и обозначают
приращения функции называют дифференциалом функции и обозначают 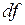 или
или 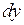 .
.
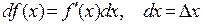 (2)
(2)
Здесь для симметрии обозначено 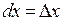 .
.
Из (2) получаем, что производная функции равна точному отношению дифференциала функции к дифференциалу независимой переменной
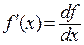
Данное выражение используется и как единый символ для обозначения производной. С учетом выражения (2) для дифференциала условие дифференцируемости можно записать
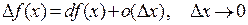 (3)
(3)
или 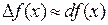 (4)
(4)
или 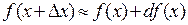 (5)
(5)
