Дифференцирование неявной функции

Функция от двух переменных называется неявной, если она задается уравнением 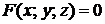, неразрешенным относительно .

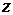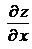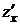Для вычисления частной производной (или ) надо зафиксировать 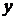и дифференцировать уравнение 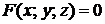, имея в виду, что 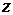зависит от 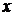. По правилу дифференцирования сложной функции получаем:

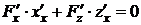, т.е. .

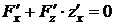Откуда

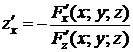или 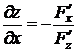. (19.10)

Аналогично

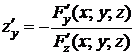или 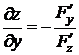. (19.11)

Если хотим, чтобы эти производные принимали определенное значение, то надо требовать, чтобы выполнялось, так называемое, условие существования неявной функции

!50. Касательная плоскость и нормаль к поверхности

Пусть имеем поверхность, заданную уравнением вида .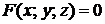

Теорема 19.3. Все касательные прямые к данной поверхности в ее обыкновенной точке 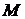лежат в одной плоскости.

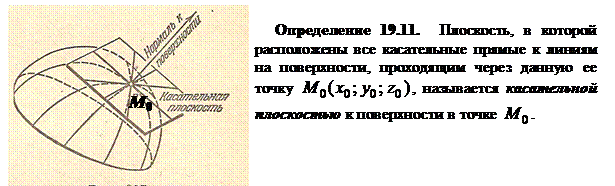
Определение 19.12. Прямая, проведенная через очку 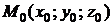поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности.

Если уравнение поверхности задано в неявном виде 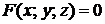, то каноническое уравнение нормали в точке 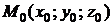имеет вид:

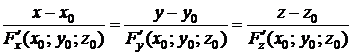. (19.14)

Если поверхность задана уравнением 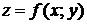, то каноническое уравнение нормали в точке 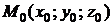имеет вид:

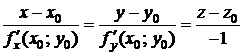. (19.15)

!51. Экстремум функции двух переменных

Понятие максимум, минимум, экстремум функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной. Пусть функция 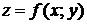определена в некоторой области 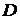, точка .

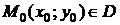Определение 19.13. Точка 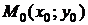называется точкой максимума 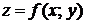, если существует такая 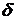-окрестность точки 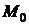, что для каждой точки 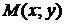, отличной от 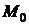, из этой окрестности выполняется неравенство

.

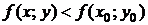Определение 19.14. Точка 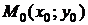называется точкой минимума 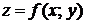, если существует такая 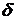-окрестность точки 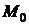, что для каждой точки 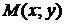, отличной от 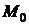, из этой окрестности выполняется неравенство

.

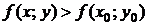Значение функции в точке максимум (минимум) называется максимум (минимум) функции. Максимум и минимум функции называют ее экстремумами.

Рассмотрим условия существования экстремума функции.

Теорема 19.4 (необходимое условие экстремума). Если точка 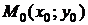является точкой экстремума функции 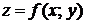, то 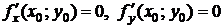или хотя бы одна из этих производных не существует.

Определение 19.15. Точки, в которых хотя бы одна частная производная равна нулю или не существует, то такие точки называются критическими точками.

Если речь идет о точках, в которых частные производные первого порядка равны нулю, то такие точки называются стационарными точками.

Теорема 19.5 (достаточное условие экстремума). Пусть функция 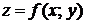имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку 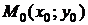. Вычислим в точке 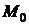значения 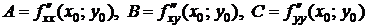. Обозначим

.

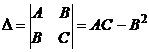!53. Основные понятия

При решении различных задач математики, физики, химии, экономики и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производную. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Так, решением уравнения 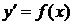является функция 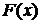- первообразная для функции .

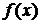Определение 20.1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную 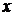, искомую функцию 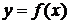и ее производные 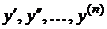. ДУ записывается так:

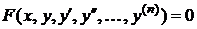
или

.

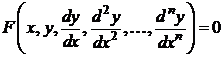Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называется обыкновенным, в противном случае – ДУ в частных производных.

Определение 20.2. Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.

Определение 20.3. Решением ДУ называется функция, которая при подстановке ее вместе с производной в это уравнение превращает его в тождество.