Дифференциальные уравнения первого порядка с раздел переменными.

Дифф уравн 1-ого порядка с раздел перемен наз уравн вида N(x)M(y)dx+P(x)Q(y)dy=0 (1)где N(x), M(y), P(x), Q(y) – ф-ии непрерывноые на некотором промежутке. Уравнение (1) разделим на произведен ф-ии P(x)M(y) и получим N(x)/P(x)dx+Q(y)/M(y)dy=0 В таком случае говорят,что переменные разделены.

Проинтегрируем его…..=с это и есть общее интегрир уравнение.

Определение. Уравнение вида

F(x,y,y',y'',…,y(n)) = 0, (*)связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у', у'',…, у(n) уравнение (*) в тождество.

Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.

Линейные дифф уравнения первого порядка.

Линейн дифф уравн1-ого порядка наз уравн вида

y’ +p(x)=f(x)

Линейные дифференциальные уравнения 1-го порядка.

y’+p(x)=q(x) (1)

y=uv, u=u(x), v=v(x) – некот. ф-ции, зав. от х подставив получим u’v+uv’+p(x)uv=q(x)

u’v+u(v’+p(x)v)=q(x)

v’+p(x)v=0 (2)

u’v=q(x) (3)

2 и 3 идут как система

v=v(x)

u’=q(x)/v(x)

u=Sq(x)/v(x)dx

Дифференц уравнения второго порядка.

Дифференциальное уравнение второго порядка можно записать в виде 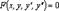. Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде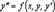

Для этих уравнений имеет место теорема существования и единственности решения.

Задачи Коши- задача нахождения решения y = у(x),удовлетворяющего заданным начальным условиям

Линейные однородные дифф уравн 2 порядка с постоянн коэффиц

Рассмотрим линейное дифференциальное уравнение вида 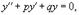где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: 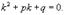Обшее решение однородного дифференциального уравнения зависит от корней уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи: ---Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией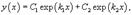

-- Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид: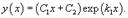

--- Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде