Линейные дифференциальные уравнения первого порядка с переменными коэффициентами
Рассмотрим линейные дифференциальные уравнения первого порядка с переменными коэффициентами. Выпишем такое уравнение в общем виде:
у¢ + a(x)y = b(x). (5.1.12)
Здесь a(x) ‑ некоторая функция аргумента x. Как мы это делали раньше, вначале будем искать решение однородного уравнения, положив функцию b(x) в правой части (5.1.12) равной нулю. Представив уравнение у¢ + a(x)y = 0 в виде
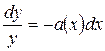 ,
,
после интегрирования получаем
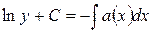
или
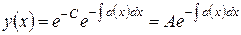 . (5.1.13)
. (5.1.13)
Здесь A ‑ неопределенная константа, которую можно найти из начального условия y(0) = 0.
Пример. Решить уравнение y’ + 2xy = 0 при начальном условии y(0) = 3.
В этом случае
a(x) = 2x, 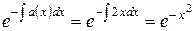
и начальное условие определяет A = 3. Искомое решение имеет вид
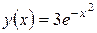 .
.
Перейдем к решению неоднородного линейного дифференциального уравнения первого порядка с переменными коэффициентами. Положим в формуле (5.1.13) A = A(x), то есть будем считать множитель A некоторой функцией от x. Этот метод называется методом вариации произвольной постоянной, и с его помощью мы попытаемся решить уравнение (5.1.12) при условии, что b(x) есть некоторая функция, не равная тождественно нулю. Из формулы (5.1.13) получаем:
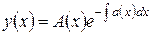 ;
; 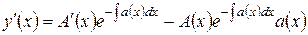 .
.
После подстановки этих выражений уравнение (5.1.12) принимает вид
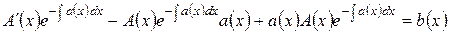 ,
,
откуда следует уравнение относительно функции 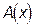 :
:
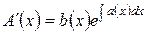 ,
,
с решением
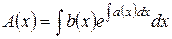 .
.
Подставив это выражение в (5.1.13), получим общее решение уравнения (5.1.12):
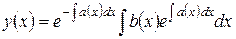 . (5.1.14)
. (5.1.14)
Пример. Решить уравнение 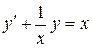 при начальном условии y(1) = 2. (Заметим, что в данном случае нельзя задавать начальное условие при x = 0, так как это значение не принадлежит области B определения функции F ).
при начальном условии y(1) = 2. (Заметим, что в данном случае нельзя задавать начальное условие при x = 0, так как это значение не принадлежит области B определения функции F ).
Для решения поставленной задачи можно было бы воспользоваться формулой (5.1.14), но мы пойдем другим путем: применим метод решения уравнений, которым была получена формула (5.1.14).
В нашем уравнении 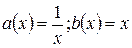 . Решение однородного уравнения
. Решение однородного уравнения 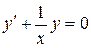 получается из формулы (5.1.13):
получается из формулы (5.1.13):
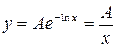 . (5.1.15)
. (5.1.15)
Реализуем теперь вариацию произвольной константы A, считая, что A = A(x) есть некоторая функция аргумента x. Тогда 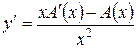 , и подставив это выражение вместе с приведенным выше выражением для y в исходное уравнение, получим:
, и подставив это выражение вместе с приведенным выше выражением для y в исходное уравнение, получим:
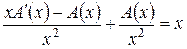 ,
,
откуда следует, что A¢(x) = x2 или 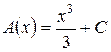 . Если теперь подставить это в формулу (12), то получится общее решение исходного уравнения:
. Если теперь подставить это в формулу (12), то получится общее решение исходного уравнения: 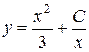 . С помощью начального условия найдем значение неопределенной константы C и выпишем решение поставленной задачи:
. С помощью начального условия найдем значение неопределенной константы C и выпишем решение поставленной задачи: 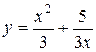 .
.
Упражнения
1.Решить дифференциальные уравнения
| 1) | 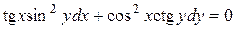 ; ; | 2) | 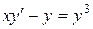 ; ; |
| 3) | 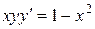 ; ; | 4) | 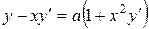 ; ; |
| 5) | 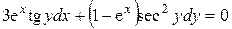 ; ; | 6) | 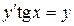 ; ; |
| 7) | 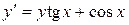 ; ; | 8) | 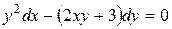 ; ; |
| 9) | 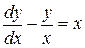 ; ; | 10) | 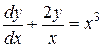 . . |
| 11) | 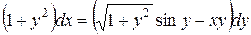 ; ; | 12) | 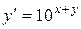 ; ; |
| 13) | 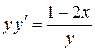 ; ; | 14) | 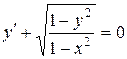 ; ; |
| 15) | 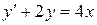 ; ; | 16) | 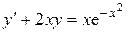 ; ; |
Раздел 6. Ряды и интеграл Фурье
Основные сведения
Функция f(x), определенная на всей числовой оси называется периодической, если существует такое число 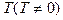 , что при любом значении х выполняется равенство
, что при любом значении х выполняется равенство 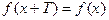 . Число Т называется периодом функции.
. Число Т называется периодом функции.
Отметим некоторые с в о й с т в а этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т.
2) Если функция f(x) период Т , то функция f(ax) имеет период 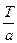 .
.
3) Если f(x) - периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство 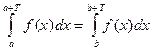 .
.
