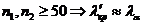Гипотеза о виде распределения

χ²-критерий Пирсона

1) Выбираются точки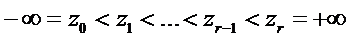

2) Согласно выдвинутой гипотезе о виде распределения – функция распределения F(x) известна – вычисляются вероятности попадания в интервалы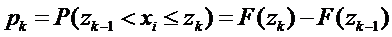

3) Обозначим 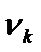– число тех x_i из выборки, которые попали в промежуток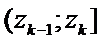

4) Тогда при справедливости основной гипотезы случайные величины 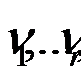имеют полиномиальное распределение с вероятностями p_i

Теперь ставится задача проверки гипотезы о том, что частоты ν_i получены из полиномиального распределения с вероятностями p_i.

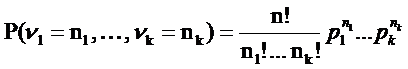
Статистика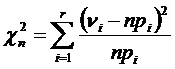

Теорема. Распределение χ_n² при nстремящемся к бесконечности сходится к χ²-распределению с (r-1) степенью свободы.

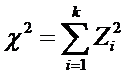
Критерий Пирсона c²

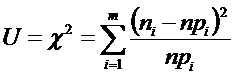
Статистика U имеет х и квадрат распределение с k = m-r-1 степенями свободы.

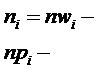Эмпирические частоты Теоретические частоты

Схема применения критерия

1. Выбирают предполагаемый закон распределения и находят его параметры (оценки параметров)

2. Определяются теоретические частоты, соответствующие опытным частотам. (n_i>10).

3. Определяется статистика c²

4. Для выбранного уровня значимости a находят критическое значение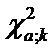

5.

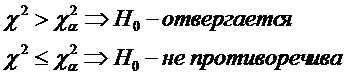
Проверка гипотез о числовых значениях параметров

Проверка гипотез о законе распределения

Вид закона распределения:

• теоретические предпосылки

• опыт аналогичных исследований

• графическое изображение эмпирического распределения

Критерий согласия:

• расхождение между опытными и теоретическими частотами несущественно и являются следствием случайности результатов единичных наблюдений или отбора отдельных элементов

• расхождения существенны, теоретический закон распределения подобран неудачно

Применение критерия согласия

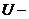Случайная величина с известным теоретическим законом распределения , характеризующая степень расхождения теоретического и эмпирического распределений.

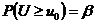
Если вероятность b мала, то это означает в соответствии с принципом практической уверенности, что такие как в опыте, и большие отклонения практически невозможны. В этом случае гипотезу Н₀ отвергают.

(обычно считают малой вероятность < 0,01)

Критерий Колмогорова

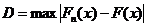
Схема применения:

1. Строятся эмпирическая функция распределения F_n(x) и предполагаемая теоретическая функция распределе-нияF(x).

2. Определяется мера расхождения между теоретичес-ким и эмпирическим распределением D и вычисляется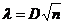

3. 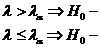отвергается.не противоречит опытным данным

Критические значения критерия Колмогорова

Замечание: В принципе применение критерия возмож-но только при полном задании теоретической функции распределения F(x).

Если задают только вид функции, а за значения пара-метров берут их оценки, то получим завышенное значе-ние вероятности P(l), а значит и большее критическое значение l_a. В результате есть риск в ряде случаев при-нят нулевую гипотезу Н₀ как правдоподобную, в то вре-мя как она противоречит опытным данным.

Проверка гипотез об однородности выборок

Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.

Пусть имеются 2 независимые выборки, произведенные из генеральных совокупностей с неизвестными теорети-ческими функциями распределения F₁(x) и F₂(x).

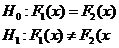
Критерий Колмогорова – Смирнова

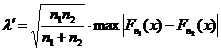
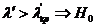Нулевая гипотеза отвергается

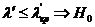Нулевая гипотеза не проти-воречит опытным данным

Замечание: практически