Критерии согласия. Проверка гипотез о виде функции распределения

Рассмотренные ранее методы оценивания параметров распределения случайной величины и критерии для проверки статистических гипотез предполагали, что известна функция распределения (нормальный закон -распределение Гаусса). Однако в большинстве случаев вид закона распределения является гипотетическим и сам по себе требует статистического подтверждения.

Наиболее простым, но весьма приближенным методом проверки согласия результатов эксперимента с тем или иным законом распределения является графический метод. Он заключается в оценке эмпирической функции распределения и сопоставлении ее с функцией предполагаемого теоретического закона. Если построенные экспериментальные точки лежат вблизи теоретического графика, то можно считать, что полученные в опытах данные не противоречат выбранному теоретическому закону распределения. Графический метод является в значительной мере субъективным и используется на практике в качестве первого приближения при решении подобных задач.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Более объективные методы установления вида распределения случайной величины строятся на аппарате проверки статистических гипотез -критериях согласия.

Нулевая гипотеза в данном случае заключается в том, что Н₀:-исследуемая генеральная совокупность не противоречит предполагаемому теоретическому закону распределения. При этом альтернативная гипотеза обычно формулируется как Hi: случайная величина имеет любое другое распределение, отличное от предполагаемого.

Разработано достаточно много критериев согласия, отличающихся как своей мощностью, так и объемом опытных данных, необходимых для их использования. Рассмотрим некоторые из них, и в первую очередь остановимся на критериях согласия, которые могут быть использованы при относительно больших объемах выборки.

Когда экспериментатор располагает достаточно представительным количеством экспериментальных данных (п > 100), то их предварительная обработка начинается с группировки, которая проводится в следующей последовательности:

1. Находят наибольшее (х_тах) и наименьшее (x_min) выборочные значения
случайной величины и вычисляют ее размах R= x_max-x_min-

2. Размах случайной величины разбивают на к равных интервалов. Количество интервалов к выбирают в зависимости от объема выборки. Например, при п >100 его значение рекомендуется принимать равным к=9-И5 (при п <100 к=7). Число интервалов к можно определить и по формуле Штюргеса k=1+3,32lg(n) с округлением полученного значения до ближайшей целой величины.

3. Определяют ширину интервала h=R/k, для упрощения расчетов полученные значения округляют в любую сторону, несколько увеличивая или уменьшая при этом размах варьирования R.

4. Устанавливают границы интервалов и подсчитывают число попаданий
случайной величины в каждый из выбранных интервалов mi, 1<i<k.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

5. Определяют частоту попаданий для каждого интервала как Pj=mi/n. Результаты подобных вычислений могут быть сведены в таблицу (подобную, например, табл. 3.5).

Таблица 3.5 Построение распределения экспериментальных данных

Интервал	Число замеров в каждом интервале m\	Частота попадания в интервал Pi= m i/n
Х1 -НХ2	m 1	mi/n
Х2-НХз	m 2	m2/n
Xj -г- Xj+1	m \	m/n
Xk + Xk+1	m к	mk/П
Проверка		k

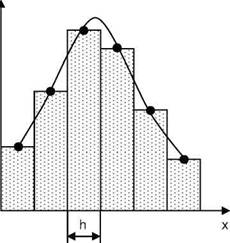
Графической формой представления непрерывной случайной величины является гистограмма (рис.3.8). Последовательность построения гистограмм следующая:

1. Определяется величина ординаты fj = Pj /h, где Pi - вероятность появления случайной величины в i-м интервале.

2. В системе координат fi=f(x) на ширине интервала h откладывают величины fi как высоты и строятся прямоугольники.

Очевидно, что площадь элементарного прямоугольника

1 г- 1 P i m i

(3.53)

S i =h-ii =h- = r{ -

h n

равна отношению числа опытов п\ при которых случайная величина оказалась внутри этого интервала, к общему числу опытов п.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

К к

Площадь всей гистограммы s = £Si = X^i = 1 ■ Следовательно, площадь,

i=l i=l ограниченная гистограммой, равна единице.

3. Построение гистограммы интегральной функции распределения

косуществляется суммированием вероятностей: F(x) = X^pi ■

f(x)

		i=l
F(x)n
i,u
		i........
	Pi						—►

X

Puc.3.8. К построению гистограммы случайной величины

В дальнейшем осуществляется сравнение экспериментально полученного распределения случайной величины с некоторым видом теоретического распределения. Для этой цели используются различные критерии согласия: _х² (хи-квадрат) Пирсона, Колмогорова-Смирнова и др.

Критерий Пирсона

Рассмотрим методику проверки гипотезы нормального распределения по критерию х² Пирсона. Этот критерий кроме определения доверительного интервала для дисперсии нередко используется для проверки согласованности распределений, полученных по данным выборки с некоторой теоретической плотностью распределения.

В данном случае применение критерия %² предполагает использование свойств нормированного (стандартного) нормального распределения. Напомним, что уравнение кривой плотности стандартного нормального распределения имеет вид

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

f 1 --²/2 пл -z²/z ^Х"^М>
j(z) = —j^e «0,4-е ;z =----------------

л/2л- <т_х

Тогда теоретическая вероятность попадания случайной величины в интервал Az=z_i+i - z\ в случае нормального распределения можно определить по формуле

P_j*-F(z_j+l)—F(z_j)- \е " ⁿdu.

2л" (3.54)

Отличие оценки закона распределения Р от теоретического закона распределения Р* можно охарактеризовать величиной

X²=ZCi(Pi-Pi*)², (3_55)

i=l

где Pi и Pi* - оценка и теоретическая вероятность случайной величины для i-ro интервала; С - весовые коэффициенты, которые с большим весом учитывают отклонения для меньших Pi.

Пирсон выбрал весовые коэффициенты следующим образом:

^ п С{

р. * . (3.56)

Пирсон показал, что при таком выборе С закон распределения %² слабо зависит от п и Р(х), а определяется в основном числом разрядов к.

Следовательно,

[P. —Pi*) ^ \m_i /п -Р;*) ^\т. -п- P_t *)

^х ~ Z-I р* ~n2-i р* ~Zj „.р* (3.57)

f=l ¹ i 1=1 ¹ i 1=1

Очевидно, что при идеальном соответствии экспериментальных данных нормальному закону распределения экспериментальное значение критерия Пирсона будет равно нулю, т.к. Pj= Pi*.

В выражении (3.55) стоит сумма квадратов к случайных величин, однако они не являются независимыми, так как на них накладывается некоторое число связей. Одной из таких связей является требование, чтобы площадь под кривой

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

коценки закона распределения равнялась единице: Z^pi=l- Иногда требуют,

i=l

чтобы среднее значение х совпадало с математическим ожиданием М_х, а выборочная дисперсия S_x² - с дисперсией а_х². Поэтому число степеней свободы чаще всего определяется как

m = к - 2. (3.58)

Теоретическое значение критерия Пирсона %²_а-_т определяется по справочным данным (см. табл.П.3) или с использованием пакетов прикладных программ при заданном уровне значимости а и числе степеней свободы m (см. функцию ХИ20БР(а;т) из электронных таблиц Microsoft Excel).

Алгоритм использования критерия Пирсона заключается в следующем.

1. Выдвигаются нуль-гипотеза Н₀: "Отличие экспериментальных данных
от нормального закона распределения не существенно" и альтернативная ей
гипотеза H-i: "Отличие экспериментальных данных от нормального закона
распределения существенно, т.е. экспериментальные данные не подчиняются
закону нормального распределения".

2. По результатам экспериментальных измерений и предположению
нормального закона их распределения определяется расчетное значение
критерия Пирсона %².

3. Определяют число степеней свободы т, задаются уровнем
значимости а и определяют теоретическое значение критерия Пирсона %²_х>т-

4. Если %²<%²<г;т, то нуль-гипотеза Н₀ о нормальном законе распределения
экспериментальных данных принимается с доверительной вероятностью Р=1-а.
В противном случае нуль-гипотеза отвергается и принимается альтернативная
гипотеза H-i.

Отметим важные рекомендации по использованию критерия %².

Если при некотором числе измерений критерий х² >%²_х-_т, но сомнения в нормальности распределения отсутствуют, то следует, если имеется возможность, увеличить число измерений в несколько раз и повторить анализ по этому же критерию.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Число степеней свободы т=к-2 относится к такому случаю, когда оба параметра нормального закона распределения определяются по результатам измерений, т.е. когда вместо точных измерений значений М_х и а_х применяют их

эмпирические значения (оценки) х и S_x. Если же значение М_х точно известно (например, при измерении эталона), то число степеней свободы равно k=n-1; если известны оба параметра М_х и а_х, то число степеней свободы равно k=n. На практике такая ситуация встречается относительно редко, и поэтому для получения числа степеней свободы не менее пяти желательно брать число интервалов не менее семи (иногда девяти).

Критерий Колмогорова–Смирнова

Рассмотрим использование критерия Колмогорова-Смирнова для проверки гипотезы нормальности распределения случайных величин. Данная процедура также предполагает построение таблицы распределения экспериментально полученных значений с группировкой данных в определенное число разрядов к. Дополнительно в таблицу необходимо включить следующие колонки:

- колонку с накопительной суммой I т^ для каждого i-ro интервала

р=1

сгруппированных данных, как показано в табл.3.6.

Таблица 3.6 Процедура вычисления критерия Колмогорова–Смирнова

Интервал	Число замеров в каждом интервале mi	Z mp p=l	Теоретичес­кая вероятность Pi*	p-\	i i * Z mp - n £ Pp p=l p=l
Х1 Н- Х2	mi	mi	P-i*	* nPj	mi-nPj
Х2Н- Хз	Ш2	m-i + m2	P2*	* * n(P!+P 2 )	(mi + тг)- * * 1 -n(Pi+P 2 )l
		…	…	… …
Xj -т- Xj+1	mi	i ____ Z m p p=l	Pi*	i * n X P p , p=l	i i * X mp - n Z Pp p=l p=l
		…	…	… …

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Хк + Хк+1

Ш|(

к ___ Z тр р=1

Рк*

к* р=1

к к % Хтр -п X Рр р=1 р=1

колонку с накопительной суммой п I Р_р, где Р*

р=1

теоретическая

вероятность попадания случайной величины в i-й интервал, значения которой, как уже отмечалось ранее, табулированы и приводятся в статистических справочниках.

На основании данных табл.3.6 вычисляют экспериментальное значение критерия согласия Колмогорова-Смирнова:

D

p-\

max

i mp-n i P_p

p-\

n

(3.58а)

Далее экспериментальное значение критерия Колмогорова-Смирнова сравнивают с теоретическим D_n;a, которое определяют из статистических таблиц в соответствии с объемом выборки п и требуемым уровнем значимости а (см. табл. П.10). Если D<D_n;a , то гипотеза о нормальном распределении результатов замеров принимается с вероятностью Р=1-а.

Критерий согласия Колмогорова-Смирнова для проверки нормальности распределения результатов наблюдений входит в пакет статистической обработки данных STATISTICA, с которым мы познакомимся в главе 7.

Рассмотрим использование рассмотренных критериев %² Пирсона и Колмогорова-Смирнова для оценки нормальности распределения данных на следующем примере.

Пример 3.8. В табл. 3.7 приведено содержание кремния в чугуне при выплавке передельного чугуна в доменной печи, которое изменяется в пределах от 0,32 до 0,95%. Всего было отобрано 50 проб чугуна.

Требуется оценить, подчиняется ли содержание кремния в пробах нормальному закону распределения? Если да, определить медиану, моду, среднее, выборочную дисперсию, доверительный интервал для математического ожидания, среднеквадратичное отклонение. Для вычислений

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

воспользуемся статистическими функциями из электронной таблицы Microsoft Excel.

Предварительно вычислим с использованием статистических функций

СРЗНАЧ, ДИСП и СТАНДОТКЛОНсреднее значение х, выборочную дисперсию S_x² и стандартное отклонение S_x, которые оказались равны

соответственно х=0,65, S_x²=0,01853 и S_x=0,1361.

Таблица 3.7 Содержание кремния в чугуне по результатам отбора 50 проб

Номер пробы
[Si],%	0,32	0,35	0,45	0,43	0,41	0,51	0,52	0,53	0,57	0,58
Номер пробы
[Si],%	0,59	0,56	0,56	0,58	0,54	0,57	0,61	0,62	0,63	0,64
Номер пробы
[Si],%	0,65	0,66	0,67	0,68	0,69	0,61	0,65	0,62	0,63	0,67
Номер пробы
[Si],%	0,65	0,62	0,68	0,71	0,72	0,78	0,75	0,72	0,79	0,72
Номер пробы
[Si],%	0,73	0,72	0,79	0,73	0,84	0,82	0,87	0,90	0,95	0,93

Примем число интервалов равным 7. Тогда величина интервала составит h=(0,95-0,32)/7=0,09=0,1. Результаты группировки исходных данных и вычислений приведены в табл. 3.8.

Таблица 3.8 Процедура вычисления критериях² Пирсона по данным примера 3.8

Интервал Xi-1-HXi	m i	F(x i )	Pf=F(Xi)-F(xM)	nPf	m i" nPf	t— „ Л2 1nPj
0,Зн-0,4		0,033	0,033	1,7	0,4	0,07
0,4н-0,5		0,135	0,102	5,1	-2,1	0,87
0,5н-0,6		0,356	0,221	11,1	-0,1	0,00
0,6н-0,7		0,642	0,286	14,3	2,7	0,51
0,7н-0,8		0,864	0,222	11,1	-0,1	0,00

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

0,8н-0,9		0,967	0,103	5,2	-1,2	0,26
0,9-И,0		0,995	0,028	1,4	0,6	0,26

Вычисление F(x) проводили с использованием статистической функции НОРМРАСП. В частности, для интервала 0,Зн-0,4 находим

НОРМРАСП(0,4;СРЗНАЧ(В4:В53);СТАНДОТКЛОН(В4:В53);ИСТИНА)=0,033.

Отметим, что поскольку среди аргументов функции НОРМРАСПесть среднее арифметическое и стандартное отклонение, то для определения

соответствующих параметров также воспользуемся встроенными функциями электронных таблиц Microsoft Excel СРЗНАЧ() и СТАНДОТКЛОН(). В показанном примере полагаем, что данные 50 опытов по содержанию кремния в чугуне расположены на листе электронной таблицы в ячейках от В4 до В53. Аналогично определяли функции распределения для каждого интервала, результаты отражены в табл. 3.8.

Таким образом, экспериментальное значение критерия Пирсона X² =2\^х] =1,96, а теоретическое при уровне значимости а=0,05 и числе

(-1

степеней свободы т₁=7-2=5 составляет х²о,о5;5=11,07 (ХИ2ОБР(0,05;5)= 11,07048), что значительно больше экспериментального значения.

Следовательно, весьма уверенно можно утверждать, что содержание кремния в пробах чугуна подчиняется нормальному закону распределения.

Предлагаем читателям самостоятельно оценить доверительный интервал математического ожидания. Здесь можно отметить, что, как показывают расчеты, доверительный интервал с вероятностью 95% равен 0,030. Учитывая близость распределения к нормальному и достаточно большое число экспериментальных точек, можно воспользоваться электронными таблицами Microsoft Excel (функция ДОВЕРИТ), т.е. действительное среднее содержание кремния в чугуне (математическое ожидание) лежит в интервале от 0,62% до 0,68%.

Процедура проверки гипотезы нормального распределения данных из примера с использованием критерия Колмогорова-Смирнова (D) представлена в табл.3.9.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Таблица 3.9 Процедура вычисления критерия Колмогорова–Смирнова по данным примера 3.8

Интервал Xi_i -e-Xj	m i	Zm p p=1	F(X)	Pf=F(Xi)--F(Xi--i)	nPf	i * n ZP p p=1		i -------i * Xm p -n XP p p=1 p=1
0,Зн-0,4			0,033	0,033	1,7	1,7	0,4
0,4н-0,5			0,135	0,102	5,1	6,8	1,8
0,5н-0,6			0,356	0,221	11,1	17,8	1,8
0,6н-0,7			0,642	0,286	14,3	32,1	0,9
0,7н-0,8			0,864	0,222	11,1	43,2	0,8
0,8н-0,9			0,967	0,103	5,2	48,4	0,3
0,9-И ,0			0,995	0,028	1,4	49,8	0,3

На основании результатов этой таблицы определяем максимальное значение из последней колонки и по нему рассчитываем экспериментальное значение критерия D:

i mp

max

p-1

p-1

D

1,8

n

=0,036. 50

Экспериментальное значение критерия сравниваем с теоретическим D5o_;o,o5 =0,177, взятым из табл. П.10 с учетом объема выборки п=50 и уровнем значимости а=0,05. Величина D₅o_;o,o5 >D, поэтому можно сделать тот же вывод, что и ранее: гипотеза нормального распределения результатов измерения содержания кремния в чугуне принимается с вероятностью 95%.

Пример 3.9.В табл. 3.10 приведено содержание оксида железа в шлаке перед раскислением металла при выплавке стали марки 0,8 КП в 200 -тонной мартеновской печи, работающей с применением кислорода для интенсификации горения топлива и прямого окисления примесей ванны. Всего отобрано 56 проб шлака.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Таблица 3.10 Исходные данные к примеру 3.9

Xj, %:	m i	1____ Zmi i=l

Z xi ' mi

x = -Ц------ = 17,375;

Zmi 1

v( ( \2

Zmj -^xj -xj^

S x = ——--------- = 16,0;

Zm i ~1 1

S x = 4,0.

Из табл. 3.10 видно, что содержание оксида железа в шлаке колеблется от 10 до 31%. Примем число интервалов равным к=7. Тогда величина интервала составит h=(31-10)/7=3. Результаты группировки исходных данных и вычислений приведены в табл. 3.11. Расчетное значение критерия Пирсона составило х²=3,861. Его следует сравнить с табличным значением %²_а-_т для 5% -ного уровня значимости, которое при числе степеней свободы, равном т=5, составляет х²о,о5;5=11,07.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Таблица 3.11 Процедура вычисления критерия %² по данным примера 3.9

Интервал Xi_i-e-Xi	m i	F(X)	Pi=F(xi)-F(xm)	nPi	rrii-nPi	(ГП| - ПР|)	2 (iTlj — nPj) nP;
10-ИЗ		0,0326 0,137	0,104	5,824	0,176	0,031	0,005
13-И 6		0,366	0,229	12,824	2,176	4,735	0,369
16-И 9		0,658	0,292	16,352	0,352	0,124	0,008
19н-22		0,876	0,218	12,208	2,208	4,875	0,399
22н-25		0,972	0,096	5,376	0,624	0,389	0,072
25н-28		0,996	0,024	1,344	0,656	0,430	0,320
28н-31		1,000	0,004	0,224	0,776	0,602	2,688
Сумма		-	-	-	-	-	E=3,861

Таким образом, опытные данные не противоречат гипотезе о том, что содержание FeO в конечном шлаке подчиняется закону нормального распределения. Оцените самостоятельно моду, медиану, доверительный интервал для математического ожидания при вероятностях 90, 95 и 99,7%.

3.7. Преобразование распределений к нормальному

Если исследователь, использовав методы, изложенные в предыдущем параграфе, убедился, что гипотеза нормальности распределения не может быть принята, то вполне может быть, что с помощью существующих методов удастся так преобразовать исходные данные, что их распределение будет подчиняться нормальному закону распределения. Для пояснения идеи преобразований рассмотрим качественный пример. Пусть кривая распределения f(x) имеет вид, представленный на рис. 3.9,а, т.е. имеются очень крутая левая ветвь и пологая правая. Такое распределение отличается от нормального.

Для выполнения операций преобразования каждое наблюдение трансформируется с помощью логарифмического преобразования x' = lg(x). При этом левая ветвь кривой распределения сильно растягивается, и распределение принимает приближенно нормальный вид (рис.3.9,б). Если при

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

преобразовании получаются значения, расположенные между 0 и 1, то все наблюдаемые значения для удобства расчетов и во избежание получения отрицательных параметров необходимо умножить на 10 в соответствующей степени, чтобы все вновь полученные, преобразованные значения были

больше единицы, т.е. необходимо выполнить преобразования x" = lg(x-10a).

V)

а

f(x')

б

^х ig(x')

х' = lg(x) Рис. 3.9. Преобразование функции f(x) к нормальному распределению

Асимметричное распределение с одной вершиной приводится к нормальному преобразованием x' = lg(x±a). В отдельных случаях можно применять и другие преобразования:

а) обратная величина х' = 1/х;

б) обратное значение квадратных корней х' = l/Vx".

Преобразование "обратная величина" является наиболее "сильным". Среднее положение между логарифмическим преобразованием и "обратной величиной" занимает преобразование "обратное значение квадратных корней".

Для нормализации смещенного вправо распределения служат, например,

степенные преобразования х' = х . при этом для а принимают значения: а=1,5 при умеренном и а=2 при сильно выраженном правом смещении. Рекомендуем читателю придумать такие преобразования, которые удовлетворяли бы исследователя в том или ином случае.

3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Контрольные вопросы

1. Какие задачи решают в ходе предварительной статистической
обработки экспериментальных данных?

2. Что такое генеральная совокупность и выборка?

3. Что такое точечное оценивание? Перечислите точечные оценки
основных параметров нормального распределения для непрерывной случайной
величины.

4. В чем заключается основная идея оценивания с помощью
доверительного интервала? С помощью каких распределений происходит
построение доверительных интервалов для математического ожидания и
дисперсии?

5. В чем заключается сущность статистических гипотез? Что такое
нулевая и альтернативная статистические гипотезы?

6. С помощью каких критериев производится отсев грубых погрешностей?

7. Какие задачи возникают при сравнении двух рядов наблюдений
экспериментальных данных? С помощью каких критериев они решаются?

8. Что такое критерий согласия? Какова основная идея его использования
при проверке гипотез о виде функции распределения?

9. В чем заключается алгоритм использования критерия Пирсона для
проверки гипотезы нормального распределения экспериментальных данных?

10. Какова процедура использования критерия Колмогорова-Смирнова
для проверки гипотезы нормального распределения?