Уравнение кривых второго порядка в полярной системе координат.

Утверждение 1. Отношение расстояния r от произвольной точки эллипса (гиперболы) до фокуса к расстоянию d от этой точки до соответствующей директрисы есть постоянная величина, равная эксцентриситету эллипса (гиперболы), т.е. .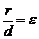

Заметим, что таким же свойством обладает и парабола, если считать .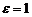

Обозначим через F фокус кривой, через 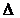– директрису. Введем полярную систему координат таким образом, что ее полюсом является точка F, а ось перпендикулярна директрисе (рис. 3).

Утверждение 2.Уравнение

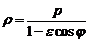(1)

во введенной системе координат определяет эллипс, если 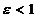; гиперболу, если 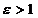и параболу, если .

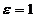Уравнение (1) называется полярным уравнением эллипса, параболы, гиперболы. В случае гиперболы это уравнение определяет одну из двух ее ветвей. Отметим, что для параболы параметр р в уравнении (1) совпадает с ее параметром р из §10, а для эллипса и гиперболы

.

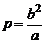17. Различные способы задания плоскости в пространстве. Взаимное расположение плоскостей. Угол между плоскостями. Расстояние от точки до плоскости.

17¹. Различные способы задания плоскости в пространстве.

Существуют различные способы задания плоскости и соответствующие им виды уравнения:

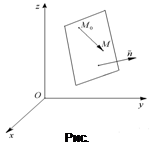1.Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Пусть заданы прямоугольная система координат Oxyz, в ней точка 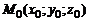и ненулевой вектор 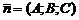. Уравнение плоскости, проходящей через точку 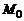перпендикулярно вектору 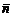(рис 1), имеет вид

.

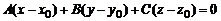2. Общее уравнение плоскости. Уравнение 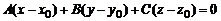преобразовывается к виду

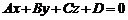, (1)

в котором .)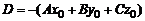

Уравнение (1) называется общим уравнением плоскости.

3.Уравнение плоскости, задаваемой тремя точкам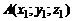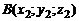и , и 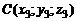Уравнение плоскости, проходящей через три данные точки.имеет вид

.

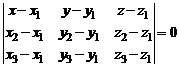4.Неполные уравнения плоскости. Общее уравнение (1) называют полным уравнением плоскости, если все его коэффициенты 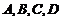отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение (1) называют неполным.

5. Уравнение плоскости в отрезках. В полном уравнении плоскости 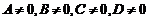. Значит, его можно переписать в виде

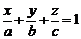, (2)

где 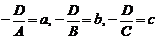. Уравнение (2) называют уравнением плоскости в «отрезках», т.к. знаменатели 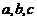есть величины отрезков, отсекаемых плоскостью на осях координат.

17². Взаимное расположение плоскостей.

Условие параллельности плоскостей (1) совпадет с условием коллинеарности векторов 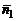и 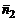и имеет вид

.

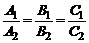Отсюда вытекает также условие совпадения плоскостей (1):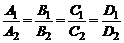

Условие перпендикулярности плоскостей (1) есть вместе с тем и условие перпендикулярности нормальных векторов 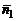и :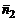

.

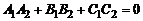17³. Угол между плоскостями.

Пусть заданы уравнения двух плоскостей:

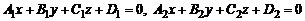. (1)

Углом между плоскостями (1) называется любой из двух смежных двугранных углов, образованных этими плоскостями.

Отметим, что сумма этих смежных двугранных углов равна 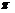. Один из этих углов определяется как угол 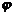между нормальными векторам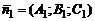и и 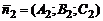к этим плоскостям:

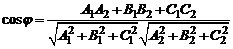. (2)

17⁴. Расстояние от точки до плоскости.

Расстояние 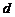от точки 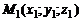до плоскости 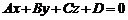находится по формуле

.

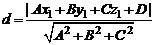18. Прямая в пространстве. Способы ее задания. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми.

18¹. Прямая в пространстве.

Прямая может быть задана пересечением двух плоскостей:

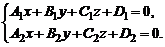(1)

если нормальные вектора этих плоскостей не коллинеарны.

18². Способы ее задания.

В зависимости от способа задания прямой в пространстве можно рассматривать различные ее уравнения.

Если известны вектор 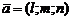, коллинеарный прямой и точка 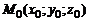, принадлежащая прямой, то прямая определяется параметрическими уравнениями:

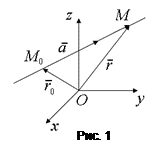
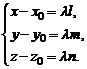(2)

Здесь 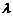– параметр.

Параметрические уравнения прямой (2) можно преобразовать к виду

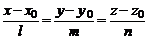. (3)

Уравнения (3) называют каноническими уравнениями прямой.

Из уравнения (3) получаем уравнение прямой, проходящей через две точк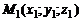и и :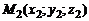

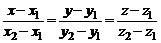. (3^/)

18³. Взаимное расположение двух прямых в пространстве.

Условие параллельности прямых (1) совпадает с условием коллинеарности векторов 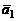и 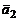. Следовательно, имеет вид

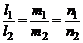. (3)

Условие перпендикулярности прямых (1) равносильно условию перпендикулярности их направляющих векторов 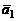и :

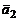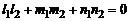. (4)

Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых), имеет вид

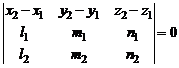. (5)

Если величины 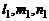не пропорциональны величинам 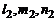, то условие (5) является необходимым и достаточным условием пересечения двух прямых в пространстве.

18⁴. Угол между двумя прямыми.

Пусть в пространстве две прямые заданы их каноническими уравнениями:

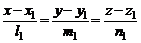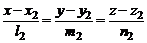, . (1)

Углом между двумя прямыми считают один из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-нибудь точку пространства. Один из этих смежных углов 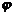равен углу между направляющими векторам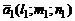и и 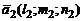данных прямых. Поэтому

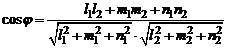. (2)