Геометрические приложения определенного интеграла в полярной системе координат

Пусть задана полярная система координат с полюсом 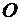и полярной осью 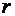(рис.56). Тогда любая точка 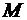на плоскости имеет в этой системе две координаты: полярный радиус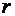 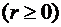, равный длине отрезка 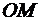, и полярный угол 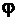, на который нужно повернуть полярную ось до совмещения с точкой 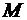. Обычно договариваются, что 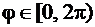. Однако это ограничение не является универсальным. Из рис. 56 видно, что

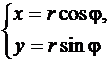(79)

и

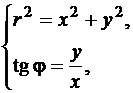(80)

причём для определения угла 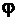следует учитывать знак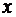и и 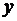. Формулы (79) и (80) устанавливают связь между полярными и декартовыми координатами точки 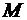для случая, когда полярная ось 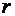совпадает с осью .

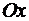2.4.1. Вычисление площади

Рассмотрим криволинейный сектор, ограниченный лучами 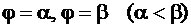и кривой 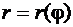(рис. 57). Вычислим его площадь.

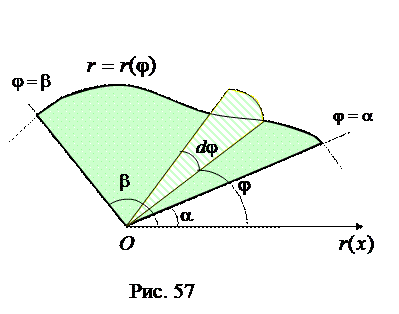
Для этого выделим элементарный криволинейный сектор, расположенный между лучами с полярным углом 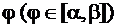и полярным углом 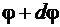. За бесконечно малый элемент площади 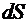примем площадь кругового сектора переменного радиуса 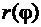с центральным углом 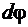. Тогда

.

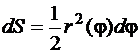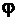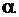Проинтегрируем полученное равенство при изменении от до 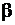и получим

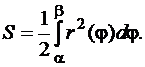(81)

Пример 4.1.1.Вычислить площадь фигуры, ограниченной линией 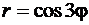, заданной в полярных координатах.

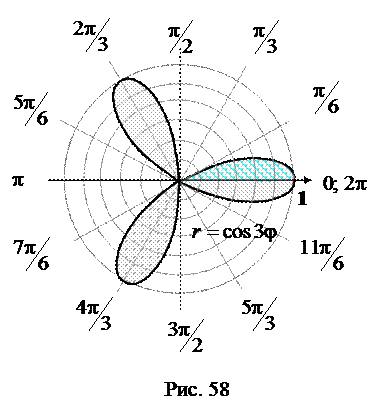
Решение. Заданная в условии линия является трехлепестковой розой (рис. 58).

Так как 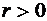, то решая неравенство 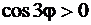, , 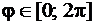найдем те значения 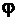, для которых она определена. Она определена для значений

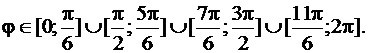
Ограниченная ею фигура состоит из трех фигур («лепестков») с одинаковой площадью. Более того, каждый из трёх «лепестков» имеет ось симметрии, делящую фигуру на две равновеликие части. Так что достаточно вычислить площадь одной из половинок «лепестка» и умножить её на 6. Рассмотрим половину «лепестка», ограниченную лучами 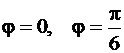. Тогда согласно формуле (81) получим

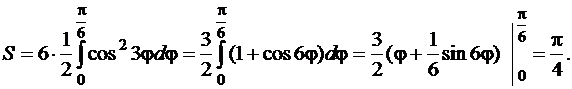
Пример 4.1.2.Вычислить площадь фигуры, ограниченной линией 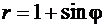, заданной в полярных координатах.

Решение. Заданная в условии линия является кардиоидой (рис. 59).

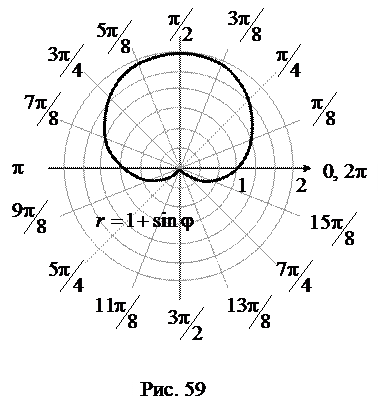
Фигура симметрична относительно луча 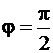(оси 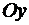). Будем вычислять площадь одной из половинок кардиоиды, заключенной между лучами 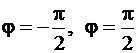, и умножать её на 2. Применяя формулу (81), получим

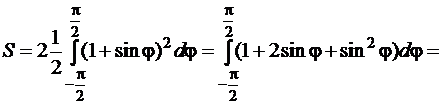
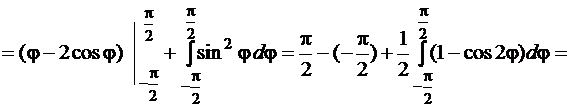
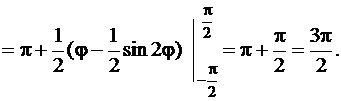
Пример 4.1.3.Вычислить площадь фигуры, ограниченной линиями 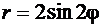, , 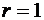заданными полярными координатами, и расположенной вне круга.

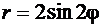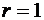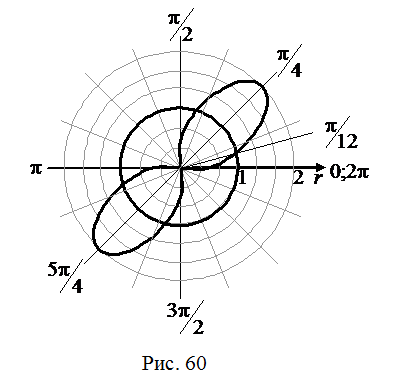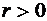Решение. Заданная в условии кривая является двухлепестковой розой, а кривая – окружностью радиуса 1 с центром в начале координат (рис. 60). Т.к. , то решая неравенство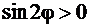 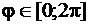, найдем те значения 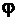, для которых двухлепестковая роза определена:

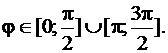
Эти два отрезка определяют два лепестка розы. При этом луч 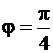делит лепесток первой четверти круга на две равные части. Так что двухлепестковая роза состоит из четырёх половинок «лепестка» одинаковой площади.

Найдём теперь координаты точки пересечения окружности и половины лепестка розы, ограниченной лучами 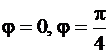. Для этого решим уравнение

.

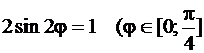Его решение 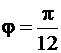. Таким образом, четвертая часть искомой фигуры заключена между лучам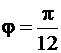и и .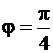

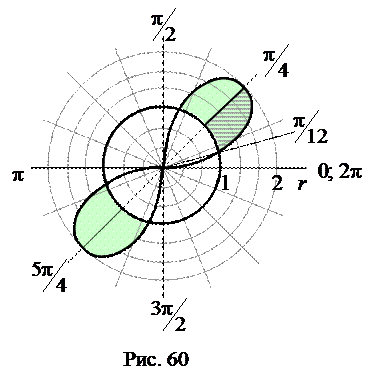
На рис. 60 эта часть заштрихована. Площадь всей фигуры получим, если площадь заштрихованной части умножим на 4.

Площадь заштрихованной фигуры будем искать как разность между площадью фигуры, ограниченной линиями 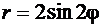, , 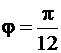, 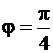и площадью сектора круга 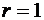, заключённого между теми же лучам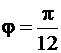и и .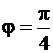

Тогда согласно формуле (81) получим

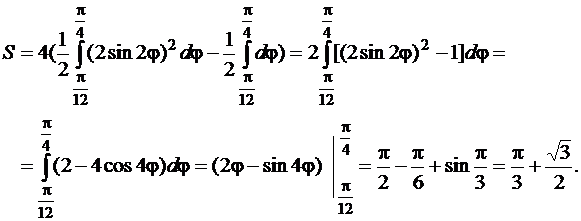
Пример 4.1.4.Вычислить площадь фигуры, ограниченной линией 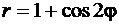, заданной в полярной системе координат.

Решение. На рис. 61 изображена заданная фигура.

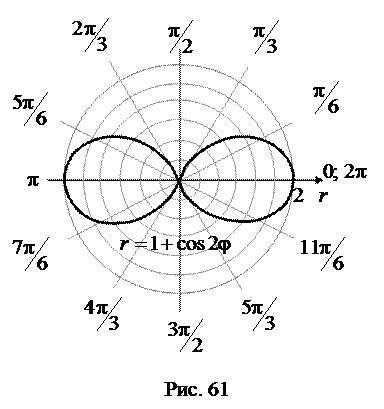
Т.к. 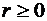для всех значений 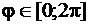, то согласно формуле (81) получим

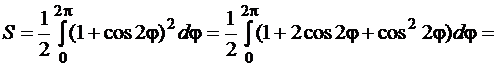
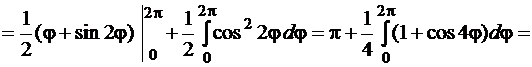
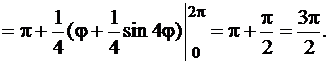
Пример 4.1.5.Вычислить площадь фигуры, ограниченной лемнискатой, заданной в полярной системе координат уравнением .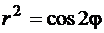

Решение. Т.к. 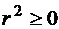, то, решая неравенство 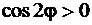( 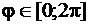), найдем те значения 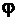, для которых заданная кривая определена. Она определена для значений

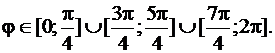
При этом в силу периодичности функции 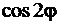лемниската обладает симметрией относительно лучей 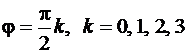(рис. 62).

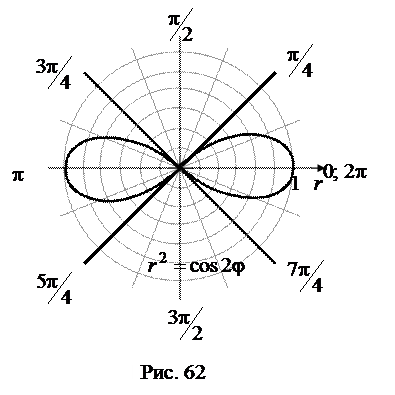
Чтобы получить площадь заданной фигуры, достаточно найти площадь её части, заключённой между лучам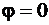и и 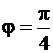, и умножить полученный результат на 4. Тогда согласно формуле (81) получим

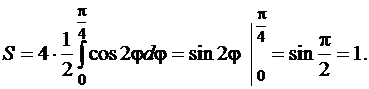
Пример 4.1.6.Вычислить площадь меньшей из фигур, ограниченных линиями, заданными в полярной системе координат уравнениями .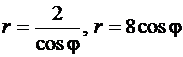

Решение. Линия 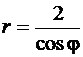(рис. 63)

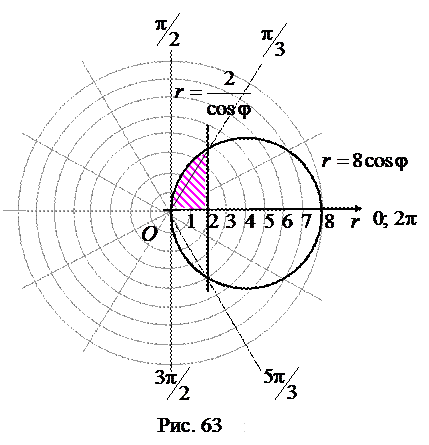
очевидным образом является прямой 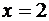(см. формулы (77) – связь полярных и декартовых координат). Линия 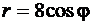представляет собой окружность с центром в точке с полярными координатами 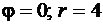и радиусом 4. Заданная фигура ограничена двумя различными линиями: прямой и окружностью. Найдем точку их пересечения. Для этого решим уравнение

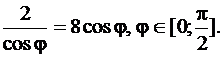
Его решением является .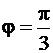

В силу симметрии заданной фигуры будем вычислять площадь её половины, расположенной в первой четверти полярной системы координат и заштрихованной на рис. 63, и умножать полученный результат на 2. Заштрихованная фигура ограничена прямой с уравнением 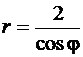при изменении переменной 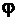от 0 до 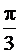, а на участке 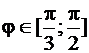– окружностью 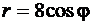. Воспользуемся теперь формулой (81) и получим:

.

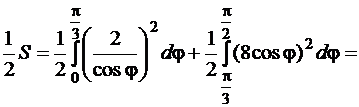
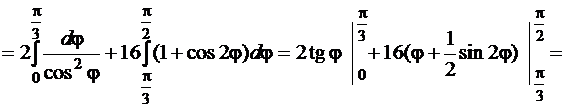
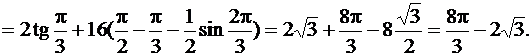
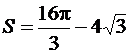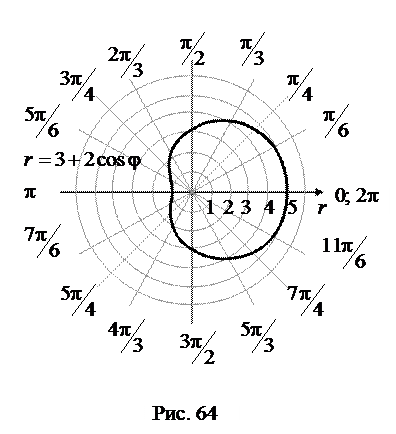
Пример 4.1.7.Вычислить площадь фигуры, ограниченной линией, заданной в полярной системе координат уравнением .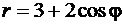

Решение. Заданная фигура изображена на рис. 64.

Функция 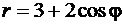определена для всех 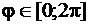. Площадь вычислим по формуле (81). Тогда

.

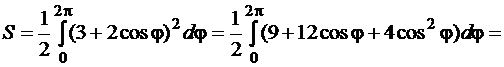
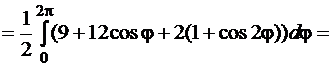
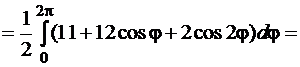
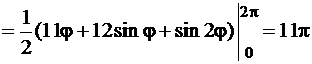2.4.2. Вычисление длины дуги

Пусть требуется найти длину дуги кривой 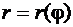, заключенной между лучами 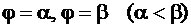(рис. 57). Для вычисления бесконечно малого элемента длины дуги воспользуемся формулой (56). Используем теперь формулы (79), связывающие полярные координаты точки на рассматриваемой дуге 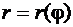с декартовыми координатами:

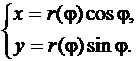
Тогда

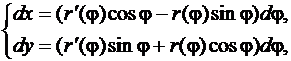
и

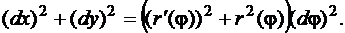
Следовательно,

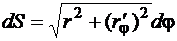, (82)

а

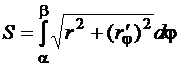. (83)

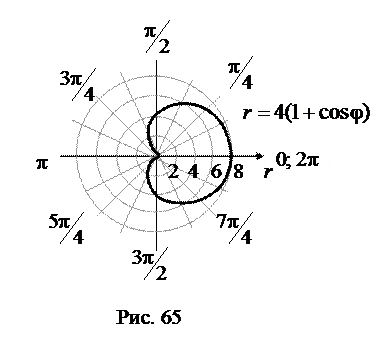
Пример 4.2.1.Найти длину дуги кардиоиды, заданной в полярной системе координат уравнением .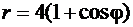

Решение. Заданная кривая изображена на рис. 65. Учтём, что кардиоида симметрична относительно полярной оси. Для того, чтобы вычислить длину всей кривой, достаточно вычислить длину её половины для 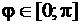и умножить результат на 2. Для нахождения бесконечно малого элемента длины дуги воспользуемся формулой (82). Найдём

,

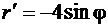а затем

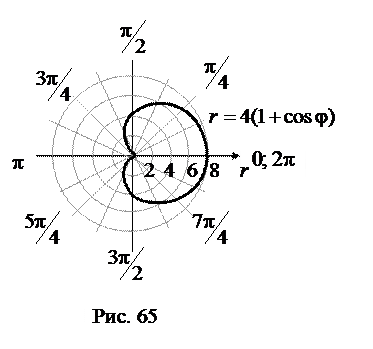
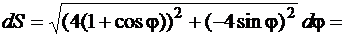
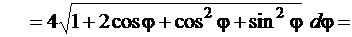
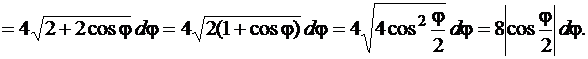
Отметим, что 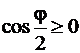для 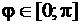. Тогда искомая длина вычисляется так

.

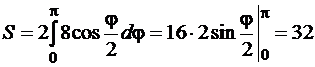Рекомендуемая литература

1. Натансон И.П. Краткий курс высшей математики./ И.П. Натансон. – СПб.: Лань, 2005.

2. Смирнова В.Б. Неопределенный интеграл: учебное пособие / В.Б. Смирнова,Л.Е. Морозова. – СПб.: СПбГАСУ, 2010.

3. Нумеров С.Н. Определённый интеграл. Методические указания к выполнению задания по курсу «Математика» для студентов всех специальностей ЛИСИ. – Л.: ЛИСИ, 1984.

4. Письменный Д.Т. Конспект лекций по высшей математике. Ч. 1. М.: Айрис-пресс, 2007.

Содержание

1.ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 3

1.1.Задача о площади криволинейной трапеции 3

1.2.Определение определенного интеграла 5

1.3.Свойства определенного интеграла, выражаемые равенствами 7

1.4.Свойства определенного интеграла, выражаемые неравенствам 10

1.5.Теорема о среднем значении 11

1.6.Теорема Барроу 14

1.7.Формула Ньютона-Лейбница. Вычисление определенного интеграла 16

1.8.Интегрирование по частям в определенном интеграле 20

1.9.Замена переменной в определенном интеграле 23

1.10.Несобственные интегралы 27

2.ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА 36

2.1.Общий подход в приложениях определенного интеграла 36

2.2.Геометрические приложения определенного интеграла 36

2.2.1.Вычисление площадей 36

2.2.2.Вычисление объёма тела через площадь его сечения 54

2.2.3.Вычисление объёма тела вращения 55

2.2.4.Длина дуги плоской кривой 69

2.2.5.Вычисление площади поверхности тела вращения 74

2.3.Механические приложения определенного интеграла 81

2.4.Геометрические приложения определенного интеграла в полярной системе координат 85

2.4.1. Вычисление площади 85

2.4.2. Вычисление длины дуги 100

Рекомендуемая литература 102

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Составители: Лидия Евсеевна Морозова

Вера Борисовна Смирнова

Редактор

Корректор

Компьютерная верстка

Подписано к печати 00.00.2005. Формат 60x84 1/16. Бум. Офсетная. Усл. печ. л. . Уч.-изд. л. . Тираж 2000 экз. Заказ . «С» . Санкт-Петербургский государственный архитектурно-строительный университет. 190005, Санкт-Петербург, 2-я Красноармейская, 4. Отпечатано на ризографе. 190005, Санкт-Петербург, 2-ая Красноармейская, 5.

[1]Функция называется кусочно-непрерывной на промежутке , если она имеет на этом промежутке конечное число разрывов I рода.

[2] В интегралах, участвующих в формуле (28), переменной интегрирования является x.