Между элементами геометрической модели векторного пространства и элементами арифметической модели векторного пространства существует взаимно однозначное соответствие (3.1), обозначим его

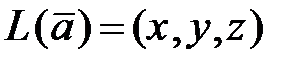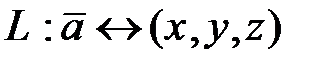, . (3.2)

Это соответствие сохраняет результат линейных операций сложения векторов и умножения на число:

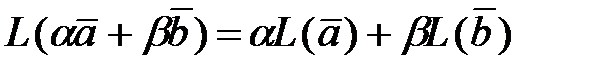(3.3)

И называется изоморфизмом арифметической и геометрической моделей векторного пространства направленных отрезков.

3.3 Определение и примеры абстрактного векторного пространства.

В этом параграфе будет построена аксиоматика и приведены примеры векторного пространства для многомерного случая N>3. Для этого заметим, что с понятием размерности N в геометрической модели направленных отрезков связана только аксиома размерности векторного пространства, в которой определено понятие базиса для случаев размерностей 1, 2 и 3. Формулировка восьми свойств операций сложения векторов и умножения векторов на число от размерности базиса не зависят. Поэтому, чтобы построить аксиоматику многомерного векторного пространства, достаточно определить понятие базиса для векторного пространства при N>3, а остальные восемь аксиом оставить без изменения.

Определение базиса и размерности векторного пространства для N>3.

Наименьший по n набор n элементов 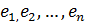из X таких, что всякий элемент x из X представляется в виде линейной комбинации

x = + + … +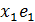

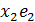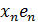
называется базисом в X, а упорядоченный набор чисел ( 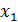, 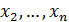) называется координатами элемента x в пространстве X.

Рассмотрим примеры объектов, удовлетворяющих этим аксиомам и являющиеся моделями многомерных векторных пространств..

Пример 1.

Множество многочленов степени не выше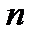

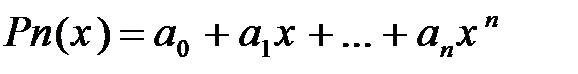
образует векторное пространство размерности n+1, в котором мономы 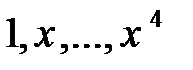– базисные элементы, а коэффициенты многочлена 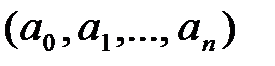– координаты вектора 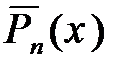в этом базисе.

Пример 2.

Пусть 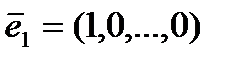, ,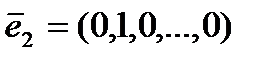…, 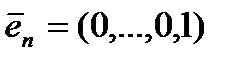- « -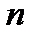местные наборы», 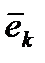имеет 1 на 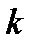-м месте и нули на остальных местах, 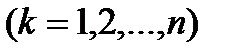. Тогда объекты

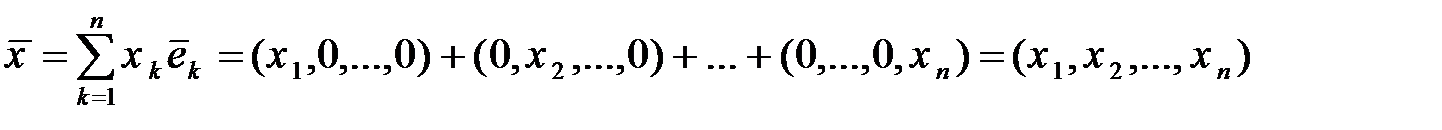
образуют векторное пространство с базисными элементами 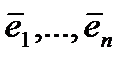. Обозначим это пространство .

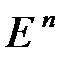Пример 3.

Объекты вида

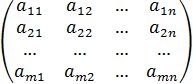=A (3.4)

называют матрицами размерности mxn, в которых элементы 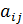стоят в i-м ряду на j-м месте. Если объекты 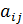– числа, то матрица называется числовой.

Такие матрицы возникают, например, если пиксельную систему экрана персонального компьютера представить в виде чисел, указав для пикселя, находящегося на пересечении i-го ряда и j-го столбца, число, соответствующее частоте (или длине) световой волны. Таким образом, любая информация, изображаемая на мониторе, представляется числовой матрицей вида (3.4).

Сумма и разность двух матриц определяется по правилу

A ± B= =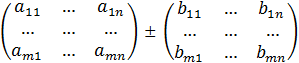

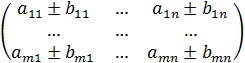= =C, (3.5)

т.е.элементы матрицы С представляют собой суммы или разности соответствующих элементов матриц А и В.

Операция умножения матрицы А на некоторое число a определяется умножением всех элементов матрицы А на это число.

Множество матриц одной размерности с только что определенными операциями образуют векторное пространство.

Учитывая определенные выше операции для матриц, заключаем, что базис этого векторного пространства образуют mxn элементов вида

где на всех местах, кроме 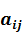, стоят нули, а 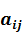=1.

С помощью этого базиса мы можем написать

А = =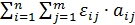

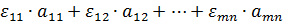
Размерность этого векторного пространства есть N=mxn.