Определение абстрактного векторного пространства.

Элементы х множества Х образуют абстрактное векторное пространство Х, если для них выполняется 8 аксиом векторного пространства относительно операций сложения элементов и умножения этих элементов на действительные числа и аксиома размерности x = 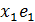+ + 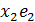… + 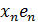, где элементы 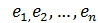образуют базис в Х.

Замечание. Пространство 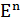построенное в примере 2 выше является арифметической или координатной моделью абстрактного векторного пространства Х размерности n. Элементы этого векторного пространства 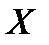могут быть произвольной природы, в чём мы убедились на примерах приведённых выше, но все они имеют одну и ту же арифметическую или, что тоже, координатную модель.

Следствие.

Все 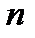-мерные абстрактные векторные пространства имеют одну и ту же арифметическую модель, поэтому изоморфны друг- другу.

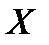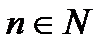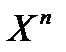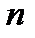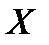Если векторное пространство содержит для всякого подмножество, , которое само является векторным пространством и для него выполняется аксиома размерности с заданным , то назовем бесконечным векторным пространством. Примером такого пространства является множество всех многочленов. Подмножества многочленов степени не выше n-1 образуют n мерные подпространства в этом пространстве.

Аксиомы скалярного произведения векторов.

Модель арифметического 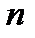-мерного пространства 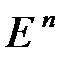не содержит понятий длинны вектора и углов между векторами. Чтобы установить понятие длины вектора и углов между векторами в пространстве размерности 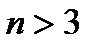рассмотрим какими свойствами определяется правило измерения длин и углов в геометрической трёхмерной модели направленных отрезков .

Напомним, что в геометрической модели трехмерного векторного пространства определяется скалярное произведение представлением

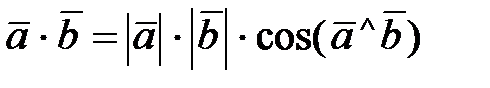(3.6)

В школьном курсе геометрии из этого представления выводятся три свойства:

1) 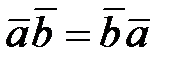, 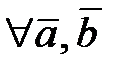(3.7)

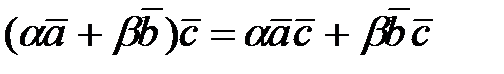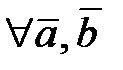2) , и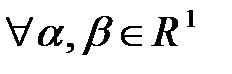

3) ; .

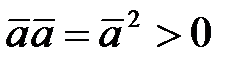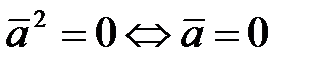Следствие.

Из формулы (3.6) находим представление длины вектора через скалярное произведение

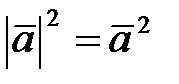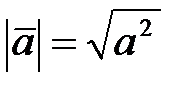, (3.8)

Если в качестве базиса выбрать векторы 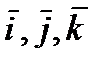, то используя свойства 1-3 скалярного произведения, получаем координатное представление скалярного произведения:

,

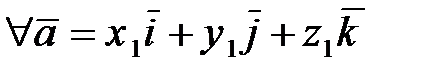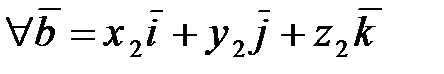
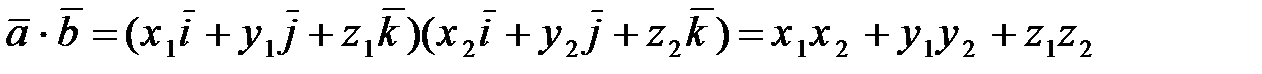(3.9)

Мы воспользовались тем, что , .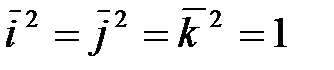

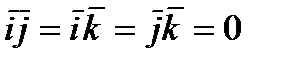Следствие.

Используя (3.8) и (3.9), заключаем, что длина трёхмерного вектора вычисляется по правилу

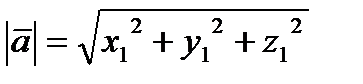(3.10)

А из формул (3.6), (3.9) и (3.10) находим формулу для вычисления углов между векторами

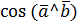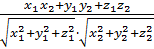= (3.11)

Вывод 4.

Вычисление длин и углов для векторов трёхмерного векторного пространства осуществляется при помощи скалярного произведения векторов. Структура скалярного произведения в трёхмерном случае определяется тремя свойствами (3.7), которые мы примем в качестве аксиом задания скалярного произведения. .

Для определения длинны вектора в 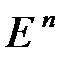при 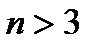воспользуемся связью между длинной вектора и скалярным произведением в трёхмерном пространстве направленных отрезков. При этом скалярное произведение зададим аксиоматически теми же свойствами, которыми оно определяется в трехмерном векторном пространстве.

Схему, по которой мы из определения скалярного произведения (3.6) получили формулу длины вектора (3.10), повторим в абстрактном векторном пространстве с той разницей, что во первых, скалярное произведение векторов зададим при помощи трех аксиом (3.7) и во вторых, существование скалярного произведения в координатной модели 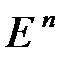установим формулой, аналогичной (3.9):

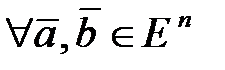
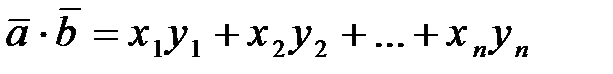(3.12)

где 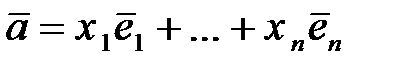, 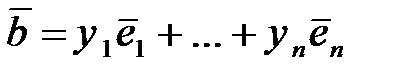в .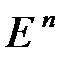

Теперь, согласно нашей схеме, длина вектора определена формулой (3.8). Из (3.8) с учетом (3.12) получаем формулу длинны вектора в 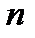-мерном арифметическом пространстве аналогичную (3.10) в виде

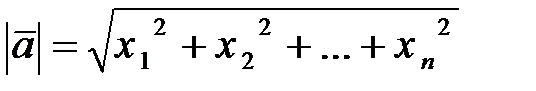. (3.13)

Формула для вычисления косинуса угла получаем в виде

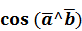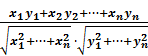= (3.14)