Однородные дифференциальные уравнения первого порядка.

Для рассмотрения однородных дифференциальных уравнений первого порядка введем понятие однородных функций.

Определение. Функция 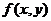называется однородной n-го измерения по своим переменным х и у, если она удовлетворяет равенству .

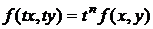Замечания:

1) Однородная функция нулевого измерения фактически зависит от отношения 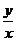, так как, если в соотношении 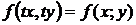считать 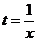, то .

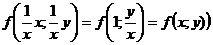2) Отношение двух однородных функций одного и того же измерения

является однородной функцией нулевого измерения.

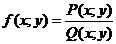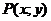Пусть , где и 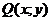однородные функции n-го измерения, то есть 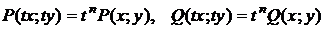, тогда .

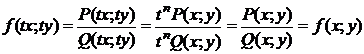Определение. Однородным дифференциальным уравнением первого порядка называется уравнение вида 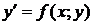(3), правая часть которого является однородной функцией нулевого измерения, то есть .

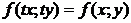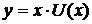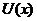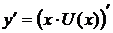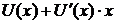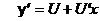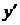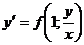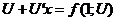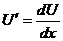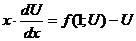Для решения однородного уравнения используется подстановка , где - неизвестная функция и = , или . Подставим выражения у и в уравнение , получим (*) - уравнение с разделяющимися переменными. Так как , то и 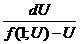= 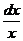- уравнение с разделенными переменными. Интегрируя последнее уравнение получим 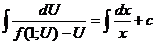- общий интеграл уравнения (*).

После нахождения 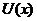необходимо вернуться к функции 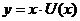и найти общий интеграл уравнения (3).

Замечания.

1. Уравнение 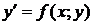является однородным, если правая часть:

1) зависит фактически от отношения ;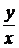

2) является отношением двух однородных функций одного измерения.

2. Уравнение вида 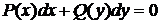является однородным, если P(x) и Q(y) - однородные функции одного измерения.

Пример. Решить уравнение .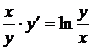

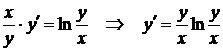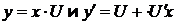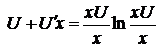
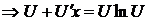Решение. . Так как , то . Так как 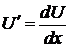, то ,

= , , .

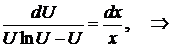
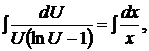
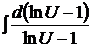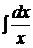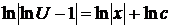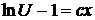Так как 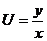, то 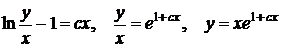- общее решение уравнения.

Лекция 14. Дифференциальные уравнения второго порядка.

Определение дифференциальных уравнений второго порядка. Основные понятия.

Линейные дифференциальные уравнения второго порядка. Фундаментальная система решений (ФСР). Теоремы об общем решении.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами их частные решения в зависимости от вида правой части. Метод вариации произвольных постоянных.

Определение дифференциальных уравнений второго порядка. Основные понятия.

Определение. Дифференциальным уравнением второго порядка называется уравнение вида 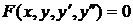(1) или .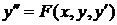

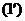Определение. Общим решением дифференциального уравнения (1) называется функция вида 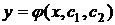, зависящая от двух произвольных постоянных 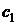и 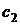и удовлетворяющая уравнению (1) при любых значениях 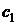и .

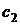Определение. Частным решением дифференциального уравнения (1) называется функция 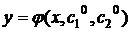, полученная из общего решения при конкретных значениях постоянных .

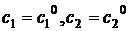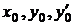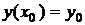Начальные условия для дифференциального уравнения второго порядка задаются с помощью трех чисел или и 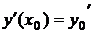. Иначе говоря задается точка 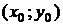и угловой коэффициент касательной 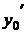к интегральной кривой в данной точке. Частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, называется решением задачи Коши.

Геометрический смысл решения задачи Коши.

Так как 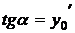, то среди интегральных кривых, проходящих через точку 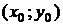, находят единственную кривую, для которой прямая с угловым коэффициентом 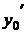, является касательной.