Определение определенного интеграла. Геометрический смысл определенного интеграла. Интегрируемость функций.

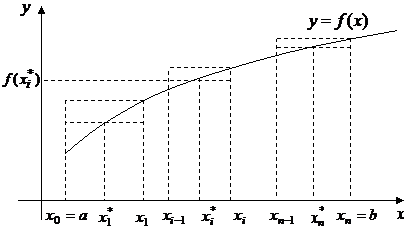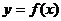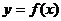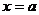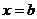Пусть функция определена и непрерывна на [a;b]. Вычислим площадь криволинейной трапеции, ограниченной кривой , осью OX и прямыми и . Разобьем отрезок [a;b] на n произвольных частей точками 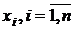так, чтобы 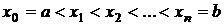.Через отмеченные точки проведем прямые, параллельные оси ординат, и получим на каждом отрезке 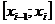криволинейную трапецию. При этом площадь всей криволинейной трапеции будет равна сумме площадей маленьких криволинейных трапеций. На каждом отрезке 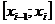выберем точку 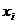и значение функции в этой точке. На отрезке 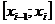строим прямоугольник высоты , площадь которого = . 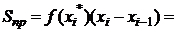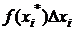Площадь этого прямоугольника примерно равна площади маленькой криволинейной трапеции.

Найдем сумму площадей всех прямоугольников. Эта сумма имеет вид 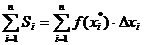и называется интегральной. Она зависит от способа разбиения отрезка [a;b] на участки 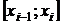и от выбора точки 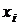на каждом участке разбиения. Интегральная сумма приближенно описывает площадь криволинейной трапеции.

Точное значение площади криволинейной трапеции мы получим, если найдем предел интегральной суммы при 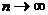и при условии, что диаметр максимального разбиения стремится к нулю, то есть .

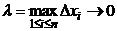Определение. Определенным интегралом функции 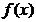на [a;b] называется предел вида .

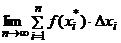Если предел конечен, то 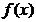называется интегрируемой на [a;b]. Этот предел не зависит от способа разбиения [a;b] на участки и не зависит от выбора точки 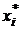на каждом участке разбиения и обозначается 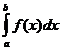, где a - нижний предел интегрирования, b - верхний предел интегрирования.

Геометрический смысл определенного интеграла.

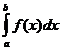численно равен площади криволинейной трапеции, ограниченной осью абсцисс, графиком 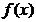и прямыми .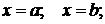

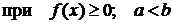Свойства определенного интеграла.

1)

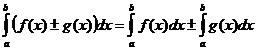
2) 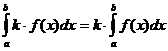, k=const

3)

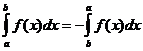
4) 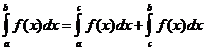, если 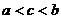- свойство аддитивности интеграла по мере

5) Интеграл от неотрицательной функции на [a;b] - неотрицательное число, то есть: если 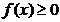на [a;b], то 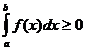- свойство знакопостоянства.

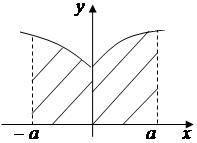6) Если 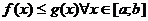, то .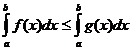

7) 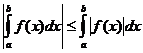при a<b.

8) .

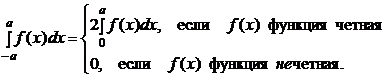9)

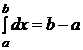
Теорема о среднем значении определенного интеграла.

Рассмотрим функцию 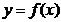интегрируемую на [a;b].

Теорема 1. Пусть функция 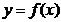на [a;b] удовлетворяет условию 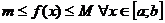, тогда .

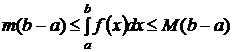Доказательство. Если 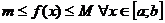, то по свойству 6 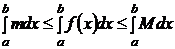. Используя свойство 2 и 9 соответственно получим, что 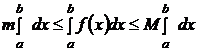и .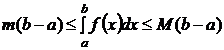

Теорема 2. Пусть функция 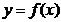интегрируема на [a;b] и на этом отрезке выполняется неравенство 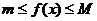, тогда существует число 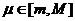, для которого .

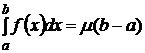Доказательство. Из теоремы 1 следует 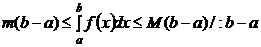, получим 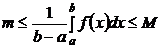. В качестве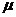 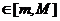возьмем число

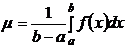, тогда .

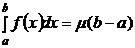Следствие из теоремы 2.

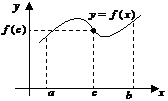Если 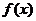непрерывна на [a;b], то существует точка 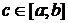, для которой выполняется равенство 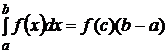, то есть площадь криволинейной трапеции равна площади прямоугольника со сторонам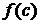и и .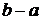

Лекция 12. Основная формула интегрального исчисления.

Определенный интеграл с переменным верхним пределом интегрирования и его свойства.

Формула Ньютона-Лейбница - основная формула интегрального исчисления.