Свойства и геометрический смысл определенного интеграла

Пусть на промежутке [a;b] задана функция f(x). Будем считать функцию непрерывной, хотя это не обязательно. Выберем на промежутке [a;b] произвольные числа x₁, x₂, x₃, ¼, x_n-1, удовлетворяющие условию:
a< x₁,< x₂<¼< x_n-1,<b. Эти числа разбивают промежуток [a;b] на n более мелких промежутков: [a;x₁], [x₁;x₂], ¼, [x_n-1;b]. На каждом из этих промежутков выберем произвольно по одной точке: c₁Î[a;x₁], c₂Î[x₁;x₂], ¼, c_nÎ[x_n-1;b].

Введем обозначения:Dx₁ = x₁ – a; Dx₂ = x₂ – x₁; ¼, Dx_n = b – x_n-1.

Составим сумму:

.

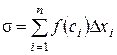Она называется интегральнойсуммой функции f(x) по промежутку [a;b]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек c_i.

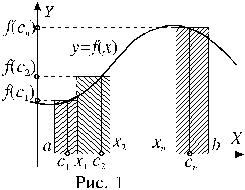
Каждое слагаемое интеграль­ной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рисунке 1.

Введем обозначение: l = max(Dx_i), i = 1, 2, ¼, n.. Величину l иногда называют параметром разбиения.

Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина l стремится к нулю. Определенным интегралом

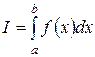
от функции 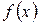по промежутку [a;b] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует:

.

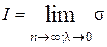Если такой предел существует, то он не зависит от первоначального разбиения промежутка [a;b] и выбора точек c_i.

Число a называетсянижним пределом интегрирования, а число b ¾ верхним пределом интегриро­вания.

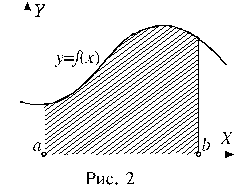
Рассмотрим фигуру, ограни­ченную графиком непрерывной, неотрицательной на промежутке [a;b] функции f(x), отрезком [a;b] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке 2 криволинейная трапеция выделена штриховкой.

Геометрический смысл определенного интеграла. Пусть функция y=f(x) непрерывна на отрезке [a; b] и f(x) ≥ 0. Фигура, ограниченная графиком функции y=f(x), прямыми x=a, x=b и осью Ох (рис. 2), называется криволинейной трапецией.

Площадь S этой трапеции определяется формулой

.

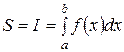Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.

Если f(x) < 0 во всех точках промежутка [a;b] и непрерывна на этом промежутке (например, как изображено на рисунке 3), то площадь криволинейной трапеции, ограниченной отрезком [a;b] горизонтальной оси координат, прямыми x = a; x = b и графиком функции y = f(x), определяется формулой

.

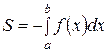Перечислим свойства определенного интеграла:

1. 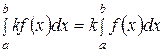(здесь k ‑ произвольное число); Если нижний и верхний пределы интегрирования равны (a=b), то интеграл равен нулю:

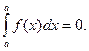
Это свойство следует из определения интеграла.

2. Если f(x)=1, то

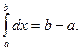
Действительно, так как f(x)=1, то

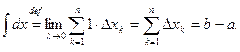
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

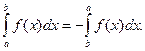
4. Постоянный множитель можно выносить за знак определенного интеграла:

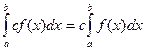
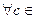R.

5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f₁(x), f₂(x), …, f_n(x) равен алгебраической сумме определенных интегралов от слагаемых:

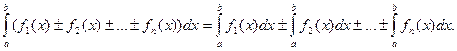
6. (аддитивность определенного интеграла). Если существует интегралы 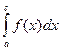и 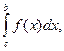то существует также интеграл 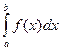и для любых чисел a, b, c;

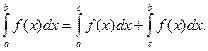
7. Если f(x) ≥ 0 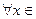[a; b], то

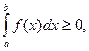a < b.

8 . (определенность определенного интеграла). Если интегрируемые функции f(x) и φ(x) удовлетворяют неравенству f(x) ≥ φ(x) 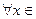[a; b], то

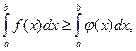a >b.

9. (об оценке определенного интеграла). Если m и М – соответственно нименьшее и наибольшее значения функции f(x), непрерывной на отрезке [a; b], то

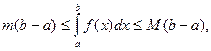a < b.

10. (теорема о среднем). Если функция f(x) непрерывна на отрезке [a; b], то существует такая точка 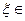[a; b], что

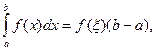
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b-a этого отрезка.

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Оказывается, что формула из пункта 4 справедлива и тогда, когда cÏ[a;b]. Пусть, например, c>b, как изображено на рисунке 4. В этом случае верны равенства

.
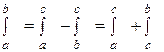