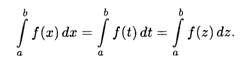Рациональная функция от sin х и cos х

Рассмотрим интеграл вида

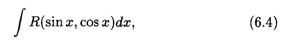
где R — рациональная функция. Этот интеграл рационализи­руется универсальной подстановкой

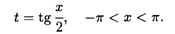
Действительно,

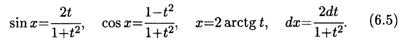
Подстановка формул (6.5) в интеграл (6.4) дает

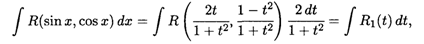
где R₁(t) — другая рациональная функция аргумента t. Рас­смотрим примеры вычисления интегралов, содержащих рацио­нальные функции от sin x и cos x.

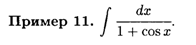
Решение. Подставляя сюда формулы (6.5), после очевид­ных упрощений получаем

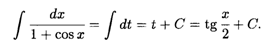
Пример 12. 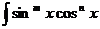dx, т и п — натуральные числа.

Решение. Универсальная подстановка приведет здесь к громоздким выкладкам; гораздо удобнее применить метод за­мены переменной. В зависимости от четности m и п употреби­мы три следующих варианта.

1) m — четное, n — нечетное, подстановка t = sin x.

2) т — нечетное, n — четное; подстановка t = cos x.

3) m и n — оба нечетные; любая из двух подстановок 1 или 2.

4) m и п — оба четные; понизить степени тригонометри­ческих функций и в полученной сумме проверить каждое сла­гаемое по пп. 1-3.

Например, найти интеграл 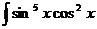dx.

Согласно п. 2 выполним подстановку t = cos x; тогда dt = - sin x dx, sin⁴ x = (1 — t²)²; отсюда имеем

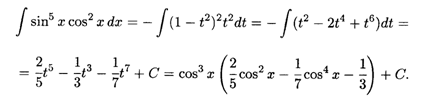
Рациональная функция от е^x

Интеграл вида

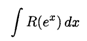
рационализируется подстановкой

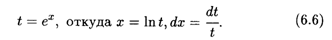
Пример 13. Найти интеграл 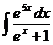. Применяя подстановку (6.6), получим

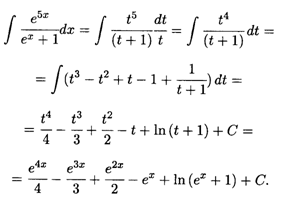
УПРАЖНЕНИЯ

Вычислить интегралы методом непосредственного интегриро­вания.

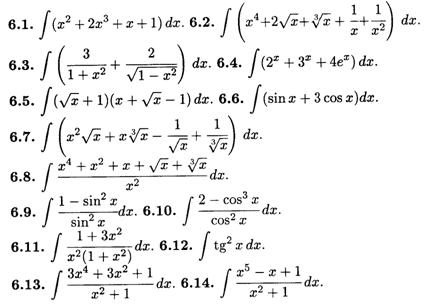
Вычислить интегралы методом подстановки.

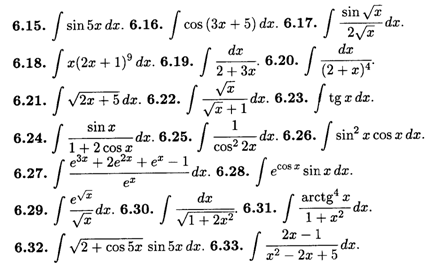
Вычислить интегралы методом интегрирования по частям.

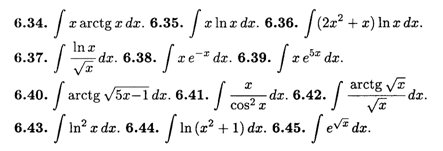
Глава 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Условия существования определенного интеграла

Определение определенного интеграла

Пусть функция f(x) задана на отрезке [а, b]. Разобьем от­резок [а, b] на п произвольных частей точками:

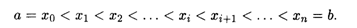
Выберем в каждом из частичных отрезков [x_i, x_i+1] произволь­ную точку ξ_i:

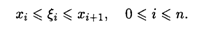
Теперь образуем сумму произведений:

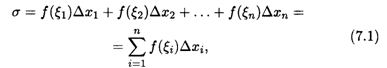
которую будем называть интегральной суммой для функции f(x) на отрезке [а, b]. Геометрический смысл величины σ ука­зан на рис. 7.1: это сумма площадей прямоугольников с основаниями Δx_i и высотами f(ξ_i) (i = 1, 2, ..., п).

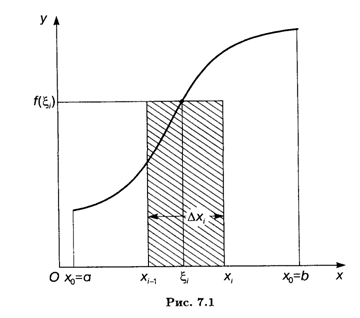
Введем еще одну величину. Обозначим через λ длину макcимального частичного отрезка данного разбиения:

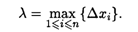
Определение. Конечный предел I интегральной суммы σ при λ → 0, если он существует, называется определенным интег­ралом от функции f(x) по отрезку [а, b]:

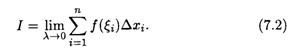
Определенный интеграл обозначается символом

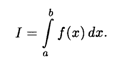
Если определенный интеграл (7.2) существует, то функ­ция f(x) называется интегрируемой на отрезке [а, b], числа а и b — соответственно нижним и верхним пределами интегри­рования, f(x) — подынтегральной функцией, х — переменной интегрирования.

Величина определенного интеграла, согласно данному вы­ше определению, однозначно определяется видом функции f(x) и числами а и b. Определенный интеграл не зависит от обозна­чения переменной интегрирования, т.е.