Классы интегрируемых функций

Ответ на вопрос о том, какие функции являются интегри­руемыми (т.е. существует определенный интеграл (7.2)), да­ют следующие теоремы, которые мы приводим без доказа­тельства.

ТЕОРЕМА 1. Если функция f(x) непрерывна на отрезке [а, b], то она интегрируема на нем.

ТЕОРЕМА 2. Если определенная и ограниченная на отрезке [а, b] функция f(x) имеет конечное число точек разрыва, то она интегрируема на этом отрезке.

ТЕОРЕМА 3. Монотонная на отрезке [а, b] функция f(x) ин­тегрируема на этом отрезке.

Основные свойства определенного интеграла

1. Интеграл 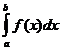был определен для случая, когда a < b. Обобщим понятие определенного интеграла и на дру­гие случаи.

По определению полагаем

как определенный интеграл на отрезке нулевой длины.

Также по определению полагаем, что

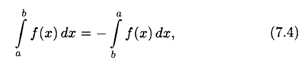
поскольку при движении от b к а все длины частичных отрез­ков Δx_i = x_i-1 — x_i имеют отрицательный знак в интегральной сумме (7.1).

2. Для любых чисел а, b и с имеет место равенство

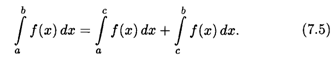
3. Постоянный множитель можно выносить за знак опреде­ленного интеграла:

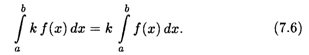
4. Определенный интеграл от алгебраической суммы функ­ций равен алгебраической сумме их определенных интегралов:

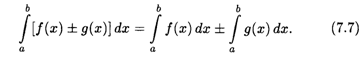
Заметим, что свойство 4 имеет место для любого конечного числа слагаемых.

Будем полагать далее, что а < b.

5. Если функция f(x) ≥ 0 всюду на отрезке [а, b], то

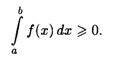
6. Если f(x) ≤ g(х) всюду на отрезке [а, b], то

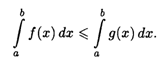
7. Если функция f(x) интегрируема на [а, b], то

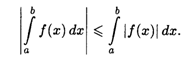
8. Если М и т — соответственно максимум и минимум функции f(x) на отрезке [а, b], то

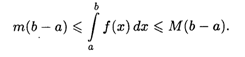
Основная формула интегрального исчисления

ТЕОРЕМА 4. Непрерывная на отрезке [а, b] функция f(x) имеет на этом отрезке первообразную. Одной из первооб­разных является функция

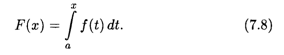
В формуле (7.8) переменная интегрирования обозначена буквой t, чтобы избежать путаницы с верхним переменным пределом х.

Поскольку всякая другая первообразная отличается от F(x) на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид

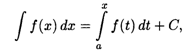
где С — произвольная постоянная.

Согласно теореме 7.4 непрерывная на отрезке [а, b] функция f(x) имеет первообразную, которая определяется формулой

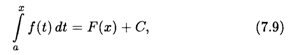
где С — некоторая постоянная. Подставляя в (7.9) х = а, с учетом свойства 1 определенного интеграла получаем

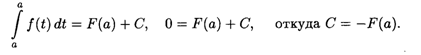
Тогда из (7.9) имеем

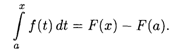
Полагая х = b, получаем формулу

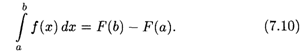
Равенство (7.10) называется основной формулой интег­рального исчисления, или формулой Ньютона-Лейбница.

Разность F(b) — F(a) условно записывают символом F(x) 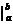, т.е.

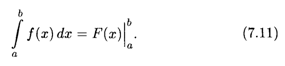
Формула (7.11) дает широкие возможности вычисления оп­ределенных интегралов. Нужно вычислить неопределенный ин­теграл и затем найти разность значений первообразной соглас­но (7.11). Рассмотрим примеры вычисления определенных ин­тегралов.

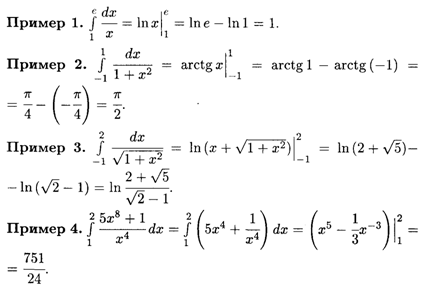
Основные правила интегрирования