Дифференцирование сложной функции
ТЕОРЕМА 3. Пусть функция х = φ(t) имеет производную в точке t0, а функция у = f(x) имеет производную в соответствующей точке x0 = φ(t0). Тогда сложная функция f[φ(t)] имеет производную в точке t0 u справедлива следующая формула:
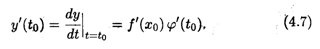
В теореме 4.3 рассмотрена суперпозиция двух функций, где у зависит от t через промежуточную переменную х. Возможна и более сложная зависимость с двумя и более промежуточными переменными, однако правило дифференцирования сложной функции остается тем же. Например, если у = у(х), х = φ(и), и = ψ(t), то производная y'(t) вычисляется по формуле
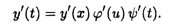
Рассмотрим несколько примеров на дифференцирование сложной функции.
Пример 1. Найти производную функции у = tg (x3).
Решение. Эту функцию можно представить через промежуточную переменную и как y = tg u, и = х3. Тогда по формуле (4.7) имеем
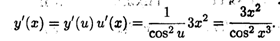
Пример 2. Найти производную функции у = 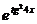 .
.
Решение. Здесь функция представляется с помощью трех промежуточных переменных: у = еu, и = v2, v = tg w, w = 4x. Применяя правило (4.7) дифференцирования сложной функции, последовательно получаем
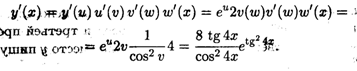
Пример 3. Найти угол наклона к оси Оx касательной к графику функции
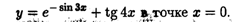
Решение. Данная функция является суммой двух сложных функций, представляемых через промежуточные переменные как
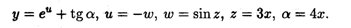
Применяя правила дифференцирования суммы функций и сложных функций, получаем
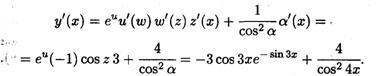
Поскольку тангенс угла наклона касательной к оси Ох при х = 0 равен значению производной в этой точке, из последнего равенства получаем, подставляя в него х = 0:
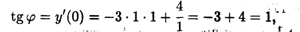
откуда φ = arctg 1 = 45°.
4.6. Понятие производной n-го порядка
Производная f'(x) функции f(x) сама является функцией аргумента х, и по отношению к ней также можно ставить вопрос о производной. Производная от первой производной некоторой функции у = f(x) называется второй производной, или производной второго порядка этой функции. Производная от второй производной называется третьей производной, или производной третьего порядка. Этот процесс можно продолжить. Производные начиная со второй называются производными высших порядков. Для их обозначения используют символы: у", у'", у(4), у(5), ..., у(n) (для второй и третьей производных соответственно еще и у(2) и у(3)) или вместо у пишут f(x): f"(x), f"(х), ..., f(n)(x).
Производная n-го порядка определяется, таким образом, как производная от производной (n — 1)-го порядка: y(n) = (y(n-1))'
Рассмотрим несколько примеров на вычисление производных высших порядков.
Пример 1. Найти производную второго порядка от функции у = х3 + 2х.
Решение. Последовательно находим первую производную, а затем и производную от нее:
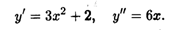
Пример 2. Найти производную второго порядка от функции 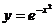 .
.
Решение. Сначала находим первую производную сложной функции:
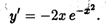
Затем ищем вторую производную, дифференцируя полученное произведение функций:
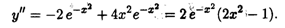
Пример 3. Найти производную третьего порядка от функции у = х In х.
Решение. Последовательно находим
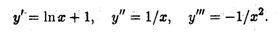
Пример 4. Найти производную n-го порядка от функции y = e2x.
Решение: Находим
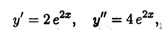
т.е. каждое дифференцирование прибавляет к исходной функции сомножитель 2. Отсюда получаем
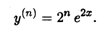
В заключение укажем формулы для вычисления производных n-го порядка для функций sin х и cos х. Нетрудно убедиться, что
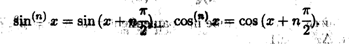
УПРАЖНЕНИЯ
Найти производные следующих функций.
4.1.у = x3 + 3x2 – 2x +1.4.2. у = 5x7 + 3x3 – 4x - 1. 4.3.у =  +
+ 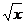 .
.
4.4. y = 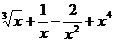 4.5. y =
4.5. y = 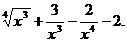
4.6. у = 3x5 + 2 sin x + 5 tg x. 4.7. у = 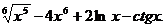 4.8. у = log2 х — 3 log3 x. 4.9. у = 3ex + arctg х — arcsin x.
4.8. у = log2 х — 3 log3 x. 4.9. у = 3ex + arctg х — arcsin x.
4.10. y = 5x + 6x + 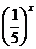 .4.11. у = x2tg x. 4.12. у=
.4.11. у = x2tg x. 4.12. у= 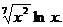
4.13. у = 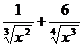 + x arccos x.4.14. у = х2log3 х - ex tg x.
+ x arccos x.4.14. у = х2log3 х - ex tg x.
4.15.у = 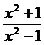 . 4.16. у =
. 4.16. у = 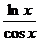 + x tg x. 4.17. y =
+ x tg x. 4.17. y = 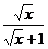 .
.
4.18. y = 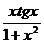 . 4.19. y =
. 4.19. y = 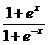 . 4.20. y =
. 4.20. y = 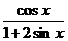 .
.
4.21. y = x2 - 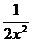 , нaйти f'(2) - f(-2)
, нaйти f'(2) - f(-2)
4.22. у = x ln x, найти f'(1), f'(e), f'(1/e), f'(1/e2).
4.23. у = sin 4x.4.24. у = cos (x2 – 2x + 1).4.25. у = sin2 х. 4.26. у = 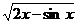 . 4.27. у = tg3 х.4.28. у = ln (x2 +
. 4.27. у = tg3 х.4.28. у = ln (x2 + 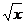 ).
).
4.29. у = arctg 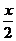 .4.30. у = ln ln x. 4.31. y = arcsin
.4.30. у = ln ln x. 4.31. y = arcsin 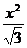 .
.
4.32. у = arctg2  . 4.33. у = esinx.4.34. у = ln2sin x.
. 4.33. у = esinx.4.34. у = ln2sin x.
4.35. у = xх.4.36. у = xcosx.
Составить уравнения касательных к графикам следующих функций.
4.37. у = x2 в точке М (1, 1).4.38. у = ln х в точке М (1, 0).
4.39. у = е2x в точке пересечения с осью Оу.
4.40. Найти угол наклона к оси Ох касательнойк гиперболеу = 1 / х в точке (1, 1).
4.41. Найти приближенное приращение функций у = х2, если x = 2 и Δx = 0,01.
4.42. С помощью дифференциалов найти приближенные значения: а) 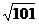 , б)
, б) 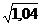 , в)
, в) 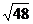 , г)
, г) 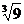 , д)
, д) 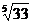 .
.
Найти производные второго порядка от функций:
4.43. у = tg х.4.44. у = sin2 x.4.45. у = 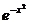 .
.
4.46. у = x sin x.4.47.у =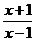 .
.
Найти производные третьего порядка от функций:
4.48. у = x e-x. 4.49. у = ex sin x.4.50. у = x ln x.
Найти производные n-го порядка от функций:
4.51. у = ln x. 4.52. у = sin 2x. 4.53. у = 3х. 4.54. у = x2 ln x. 4.55. у = х cos x. 4.56. у = x3еx.
