Непрерывность элементарных функций

Непрерывность элементарных функций в точке

Постоянная функция f(x) = С является непрерывной в лю­бой точке числовой прямой. Действительно, 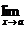f(x) = С = f(а), что соответствует определению непрерывности функ­ции в точке.

Функция f(x) = х непрерывна в каждой точке а числовой прямой, так как предел функции в точке а равен еезначению в этой точке: 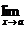f(x) = а = f(a).

Из сказанного выше и теоремы 3.7 следует, что в любой точке числовой прямой функции x² = x ∙ x, x³ = x² ∙ х,..., xⁿ = x^n-1 ∙ x (n — натуральное число) непрерывны.

Алгебраический многочлен

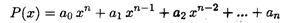
также является непрерывной функцией в любой точке число­вой прямой в силу теоремы 3.7, поскольку представляет собой сумму произведений непрерывных функций.

Дробно-рациональная функция

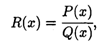
где Р(x) и Q(x) — алгебраические многочлены, в силу теоремы 3.7 непрерывна во всех точках числовой прямой за исключени­ем корней знаменателя.

Тригонометрические функцииsin x, и cos x непрерывны в любой точке x числовой прямой.

Непрерывность функций tg x = sin x / cos x и sec x = 1/ cos x соблюдается во всех точках, x ≠ π / 2 + nπ; аналогично непре­рывность функций ctg x = cos x / sin x и sec x = 1 / sin x обеспе­чена во всех точках x ≠ пπ (n = 0, ±1, ±2,...).

Рассмотренные выше функции непрерывны в каждой точ­ке, в окрестности которой они определены. В силу теоремы 3.7 функции, получаемые из них при использовании конечного чис­ла арифметических операций, являются также непрерывными.

Непрерывность функции на интервале и отрезке

Говорят, что функция f(x) непрерывна на интервале (а, b), если она непрерывна в каждой точке этого интервала. Функ­ция f(x) непрерывна на отрезке [а, b], если она непрерывна на интервале (а, b) и непрерывна в точке a справа, а в точке b слева:

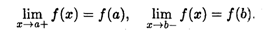
Классификация точек разрыва функции

Точки разрыва, в которых функция не является непрерыв­ной, классифицируются следующим образом.

1. Устранимый разрыв.Точка а называется точкой устранимого разрыва функции f(x), если предел функции в этой точке существует, но в точке а функция f(x) либо не опре­делена, либо ее значение f(а) не равно пределу в этой точке.

Пример 1. Функция f(x) = 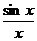в точке х = 0, как известно, имеет предел, равный единице (первый замечательный пре­дел). Однако в самой точке х = 0 эта функция не определе­на, т.е. здесь разрыв первого вида. Этот разрыв можно устра­нить (потому он и называется устранимым), если доопреде­лить функцию в этой точке значением предела в ней, т.е. ввес­ти новую функцию

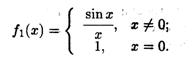
Функция f₁(x) является непрерывной на всей числовой прямой.

2. Разрыв первого рода. Точка а называется точкой раз­рыва первого рода функции f(x), если в этой точке функция имеет конечные, но не равные друг другу левый и правый пре­делы:

.

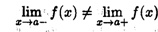Пример 2. Рассмотрим функцию

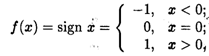
для нее точка х = 0 является точкой разрыва 1-го рода.

3. Разрыв второго рода. Точка а называется точкой раз­рыва второго рода функции f(x), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних преде­лов или хотя бы один из односторонних пределов бесконечен.

Пример 3. Для функции f(x) = 1/x точка х = 0 является точ­кой разрыва 2-го рода, поскольку .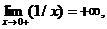

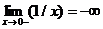Пример 4. Для функции f(x) = sin (l/x) точка х = 0 явля­ется точкой разрыва 2-го рода, так как ни левого, ни правого предела функции в этой точке не существует.

Пример 5. Рассмотрим функцию f(x) = е¹/^x = ехр 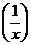(рис. 3.8). Точка х = 0 является точкой разрыва 2-го рода для этой функции, так как предел слева равен нулю, а предел справа бесконечен:

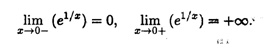
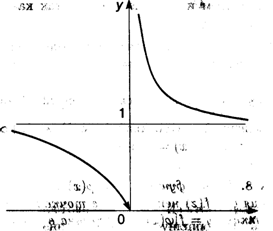
Рис. 3.8

Понятие сложной функции

Определение. Если на некотором промежутке Х определена функция z = φ(x) с множеством значений Z и на множестве Z определена функция у = f(z), то функция у = f[φ(x)] называ­ется сложной функцией от x (или суперпозицией функций), а переменная z — промежуточной переменной сложной функции.

Приведем примеры сложных функций.

Пример 1.у = cos 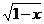—сложная функция, определенная на полубесконечном интервале (— ,1], так как у = f(z) = cos z, z = φ(x) = .

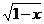Пример 2. у = 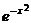— сложная функция, определенная на всей числовой прямой, поскольку у = f(z) = е^z , z = φ(x) = —х².

Пример 3. у= 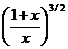— сложная функция, определенная на полубесконечных интервалах (- ,0) и (0, + ), так как y = f(z) = z^3/2, z = φ(x) = (1 + x) / x.

ТЕОРЕМА 8. Пусть функция z = φ(x) непрерывна в точке x₀, а функция у = f(z) непрерывна в точке z₀ = φ(x₀). Тогда сложная функция у = f[φ{x)] непрерывна в точке x₀ = 0.

Пример 4. Функция y = tg (x² + 2x) непрерывна в точке x = 0, так как функция z = х² + х непрерывна в точке х = 0, а функ­ция у = tg z непрерывна в точке z = 0.