Числовые последовательности и операции над ними
Числовые последовательности представляют собой бесконечные множества чисел. Примерами последовательностей могут служить: последовательность всех членов бесконечной геометрической прогрессии, последовательность приближенных значений 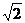 (x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности.
(x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности.
Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,... поставлено в соответствие вещественное число xп, то множество вещественных чисел
x1, x2, x3, …, xn, … (2.1)
называется числовой последовательностью, или просто последовательностью. .
Числа х1, x2, x3, ..., xп, ... будем называть элементами, или членами последовательности (2.1), символ xп — общим элементом, или членом последовательности, а число п — его номером. Сокращенно последовательность (2.1) будем обозначать символом {хп}. Например, символ {1/n} обозначает последовательность чисел
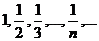 .
.
Иными словами, под последовательностью можно понимать бесконечное множество занумерованных элементов или множество пар чисел (п, xп), в которых первое число принимает последовательные значения 1, 2, 3, ... . Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула xп = -1 + (-1)n определяет последовательность 0, 2, 0, 2,... .
Геометрически последовательность изображается на числовой оси в виде последовательности точек, координаты которых равны соответствующим членам последовательности. На рис. 2.1 изображена последовательность {хп} = {1/n} на числовой прямой.

Понятие сходящейся последовательности
Определение 2. Число а называется пределом последовательности {xn}, если для любого положительного числа ε существует такой номер N, что при всех п > N выполняется неравенство
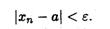 (2.2)
(2.2)
Последовательность, имеющая предел, называется сходящейся. Если последовательность имеет своим пределом число а, то это записывается так:
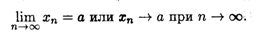
Последовательность, не имеющая предела, называется расходящейся.
Определение 3. Последовательность, имеющая своим пределом число а = 0, называется бесконечно малой последовательностью.
Замечание 1. Пусть последовательность {хп} имеет своим пределом число а. Тогда последовательность {αn}= {xn — a} есть бесконечно малая, т.е. любой элемент xп сходящейся последовательности, имеющей предел а, можно представить в виде
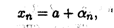
где αn — элемент бесконечно малой последовательности {αn}.
Замечание 2. Неравенство (2.2) эквивалентно неравенствам (см. свойство 4 модуля числа из п. 1.5)
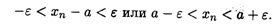

Это означает, что при п > N все элементы последовательности {xn} находятся в ε-окрестности точки а (рис. 2.2), причем номер N определяется по величине ε.
Интересно дать геометрическую интерпретацию этого определения. Поскольку последовательность представляет собой бесконечное множество чисел, то если она сходится, в любой ε-окрестности точки а на числовой прямой находится бесконечное число точек — элементов этой последовательности, тогда как вне ε-окрестности остается конечное число элементов. Поэтому предел последовательности часто называют точкой сгущения.
Замечание 3. Неограниченная последовательность не имеет конечного предела. Однако она может иметь бесконечный предел, что записывается в следующем виде:
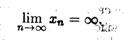 (2.3)
(2.3)
Если при этом начиная с некоторого номера все члены последовательности положительны (отрицательны), то пишут
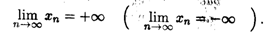
Если {xn} — бесконечно малая последовательность, то {1/xп} — бесконечно большая последовательность, имеющая бесконечный предел в смысле (2.3), и наоборот.
Приведем примеры сходящихся и расходящихся последовательностей.
Пример 1. Показать, используя определение предела последовательности, что 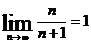 .
.
Решение. Возьмем любое число ε > 0. Так как
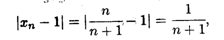
то чтобы выполнялось неравенство (2.2), достаточно решить неравенство 1 / (n + 1) < ε, откуда получаем n > (1 — ε) / ε. Достаточно принять N = [(1 — ε)/ε] (целая часть числа (1 — ε)/ ε)* , чтобы неравенство |xп — 1| < ε выполнялосьпривсех п > N.
* Символ [a] означает целую часть числа а, т.е. наибольшее целое число, не превосходящееа. Например,[2] = 2, [2,5] = 2, [0,8] = 0, [-0, 5] = -1, [-23,7] = -24.
Пример 2. Показать, что последовательность {хп} = (-1)n, или -1, 1, -1, 1,... не имеет предела.
Решение. Действительно, какое бы число мы ни предположили в качестве предела: 1 или —1, при ε < 0,5 неравенство (2.2), определяющее предел последовательности, не удовлетворяется — вне ε -окрестности этих чисел остается бесконечное число элементов xп: все элементы с нечетными номерами равны —1, элементы с четными номерами равны 1.
Основные свойства сходящихся последовательностей
Приведем основные свойства сходящихся последовательностей, которые в курсе высшей математики сформулированы в виде теорем.
1. Если все элементы бесконечно малой последовательности {хп} равны одному и тому же числу с, то с = 0.
2. Сходящаяся последовательность имеет только один предел.
3. Сходящаяся последовательность ограничена.
4. Сумма (разность) сходящихся последовательностей {хп} и {уп} есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей {xп} и {yп}.
5. Произведение сходящихся последовательностей {хп} и {уп} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {хп} и {уп}.
6. Частное двух сходящихся последовательностей {хп} и {уп} при условии, что предел последовательности {уп} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {хп} и {yп}.
7. Если элементы сходящейся последовательности {хn} удовлетворяют неравенству xп ≥ b (хп ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ b (а ≤ b).
8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность.
9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Рассмотрим применение этих свойств на примерах.
Пример 3. Найти предел 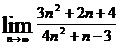 .
.
Решение. При n 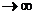 числитель и знаменатель дроби стремятся к бесконечности, т.е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на n2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим
числитель и знаменатель дроби стремятся к бесконечности, т.е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на n2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим
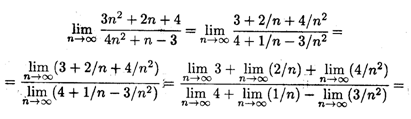
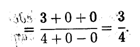
Пример 4. Найти предел последовательности {xп} = 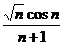 при п
при п 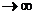 .
.
Решение. Здесь, как и в предыдущем примере, числитель и знаменатель не имеют конечных пределов, и потому сначала необходимо выполнить соответствующие преобразования. Поделив числитель и знаменатель на n, получаем
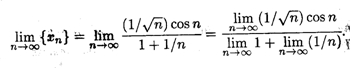
Поскольку в числителе стоит произведение бесконечно малой последовательности на ограниченную последовательность,то в силу свойства 8 окончательно получаем
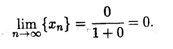
Пример 5. Найти предел последовательности {хп} = 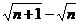 при п
при п 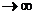 .
.
Решение. Здесь применить непосредственно теорему о пределе суммы (разности) последовательностей нельзя, так как не существует конечных пределов слагаемых в формуле для {хп}. Умножим и разделим формулу для {хn} на сопряженное выражение 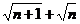 :
:
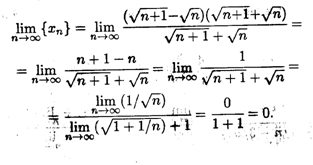
Число е
Рассмотрим последовательность {хп}, общий член которой выражается формулой
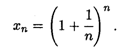
В курсе математического анализа доказывается, что эта последовательность монотонно возрастает и имеет предел. Этот предел называют числом е. Следовательно, по определению
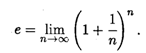
Число е играет большую роль в математике. Далее будет рассмотрен способ его вычисления с любой требуемой точностью. Отметим здесь, что число е является иррациональным; его приближенное значение равно е = 2,7182818... .
Применение в экономике
Рассмотрим два примера из экономики на использование числа е.
Пример 1. Известно, что формула сложных процентов имеет вид
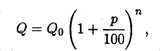 (2.4)
(2.4)
где Q0 — первоначальная сумма вклада в банк, р — процент начисления за определенный период времени (месяц, год), п — количество периодов времени хранения вклада, Q — сумма вклада по истечении п периодов времени. Формулы типа (2.4) используются также в демографических расчетах (прирост народонаселения) и в прогнозах экономики (увеличение валового национального продукта). Пусть первоначальный депозит Q0 помещен в банк под р = 100% годовых, тогда через год сумма депозита составит 2Q0. Предположим, что через полгода счет закроется с результатом 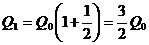 и эта сумма будет вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять
и эта сумма будет вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять 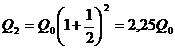 . Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия. При ежеквартальном повторении этих операций депозит в конце года составит
. Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия. При ежеквартальном повторении этих операций депозит в конце года составит 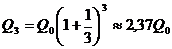 . Если повторять операцию изъятие-размещение в течение года сколько угодно раз, то при ежемесячном манипулировании сумма за год составит
. Если повторять операцию изъятие-размещение в течение года сколько угодно раз, то при ежемесячном манипулировании сумма за год составит 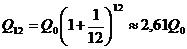 ; при ежедневном посещении банка
; при ежедневном посещении банка 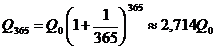 ; при ежечасном —
; при ежечасном — 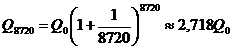 и т.д. Нетрудно видеть, что последовательность значений возрастания первоначального вклада {qn} = {Qn/Q0} как раз совпадает с последовательностью, пределом которой является число ε при п
и т.д. Нетрудно видеть, что последовательность значений возрастания первоначального вклада {qn} = {Qn/Q0} как раз совпадает с последовательностью, пределом которой является число ε при п 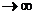 согласно (2.4). Таким образом, доход, который можно получить при непрерывном начислении процентов, может составить за год не более чем
согласно (2.4). Таким образом, доход, который можно получить при непрерывном начислении процентов, может составить за год не более чем
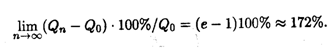
В общем случае, если р — процент начисления и год разбит на n частей, то через t лет сумма депозита достигнет величины
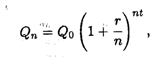
где r = р/100. Это выражение можно преобразовать:
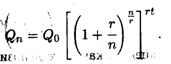
Мы можем ввести новую переменную 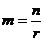 и при n
и при n 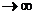 получим m
получим m 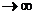 ,или
,или
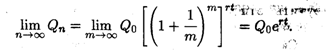
Расчеты, выполненные по этой формуле, называют вычислениями по непрерывным процентам.
Пример 2. Пусть темп инфляции составляет 1% в день.Насколько уменьшится первоначальная сумма через полгода?
Решение. Применение формулы сложных процентов дает
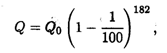
где Q0 — первоначальная сумма, 182 — число дней в полугодии. Преобразуя это выражение, получаем
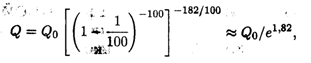
т.е. инфляция уменьшит первоначальную сумму примерно в 6 раз.
УПРАЖНЕНИЯ
Найти пределы следующих последовательностей.
2.1. 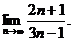 2.2.
2.2. 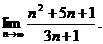 2.3.
2.3. 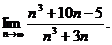 2.4.
2.4. 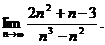 2.5.
2.5. 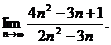 2.6.
2.6. 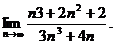 2.7.
2.7. 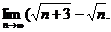 2.8.
2.8. 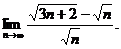
2.9. Прирост населения страны составляет р процентов в год. За сколько лет население страны удвоится? Дать ответ при а) р = 3% и б) р = 5%.
2.10. Коммерческий банк, обслуживающий предприятие по выдаче заработной платы, задерживает перечисляемые ему средства в среднем на 9 месяцев. За это время он успевает три раза "прокрутить" эти деньги в виде краткосрочных кредитов, выдаваемых частным предпринимателям на три месяца, под 3% в месяц. Сколько процентов прибыли получает банк на этой операции?
2.11. В условиях предыдущей задачи рассчитать, что выгоднее банку: кредитовать из собственных средств предприятия на условиях ставки годового процента, равной 20%, или заниматься вышеуказанной деятельностью.
2.12. Темп инфляции составляет 6% в месяц. Каков должен быть процент годовой ставки кредита, выдаваемого банком, чтобы прибыль от кредитования составляла 12% в год?
Глава 3. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Понятие функции
Определение функциональной зависимости
Определение 1. Пусть Х и Y — некоторые числовые множества и пусть каждому элементу x 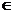 Х по какому-либо закону f поставлен в соответствие один элемент у
Х по какому-либо закону f поставлен в соответствие один элемент у 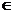 Y. Тогда будем говорить, что определена функциональная зависимость у от x по закону у = f(x). При этом x называют независимой переменной (или аргументом), у — зависимой переменной, множество Х — областью определения (существования) функции, множество Y — областью значений (изменения) функции.
Y. Тогда будем говорить, что определена функциональная зависимость у от x по закону у = f(x). При этом x называют независимой переменной (или аргументом), у — зависимой переменной, множество Х — областью определения (существования) функции, множество Y — областью значений (изменения) функции.
Кроме буквы f для обозначения функции используются и другие буквы, другими буквами может обозначаться также и независимая переменная. Примеры записи функций: у = у (x), y = F(x), y = g(x).
Если множество Y значений функции ограничено, то функция называется ограниченной, в противном случае — неограниченной.
Способы задания функций
Задать функцию — значит указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие (вычисляется) значение зависимой переменной из области значений функции. Существуют три основных способа задания функций: табличный, аналитический и графический.
1. Табличный способ. Этот способ имеет широкое применение в разных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т.п. Как правило, в таких таблицах по крайней мере одну из переменных можно принять за независимую (например, время), тогда другие величины будут являться функциями от этого аргумента. По сути дела базы данных основаны на табличном способе задания, хранения и обработки информации, а значит, и на табличной форме функциональной зависимости.
2. Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде формул. Следует подчеркнуть, что функция может определяться и набором формул — на разных промежутках области определения функции используются разные формулы.
Приведем примеры аналитического задания функций.
Пример 1. у = х3. Эта функция задана на бесконечной прямой -  < x <
< x <  . Множество значений этой функции тоже бесконечная числовая прямая -
. Множество значений этой функции тоже бесконечная числовая прямая -  < у <
< у <  . Функция называется кубической параболой (рис. 3.1).
. Функция называется кубической параболой (рис. 3.1).
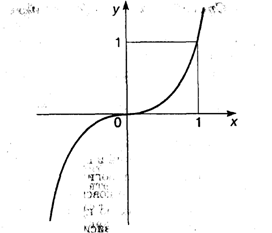
Рис. 3.1
Пример 2. у = 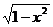 . Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окружности, лежащая в верхней полуплоскости (рис. 3.2).
. Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окружности, лежащая в верхней полуплоскости (рис. 3.2).
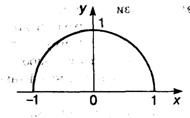
Рис. 3.2
 +1, если x > 0;
+1, если x > 0;
Пример 3. у = sign x = 0, если х = 0;
-1, если х < 0.
Термин sign происходит от латинского signum — знак. Функция задана на всем бесконечном промежутке (-  ,
,  ), а область ее значений состоит из трех чисел: —1, 0, 1 (рис. 3.3).
), а область ее значений состоит из трех чисел: —1, 0, 1 (рис. 3.3).
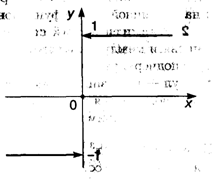
Рис. 3.3
Стрелки означают, что полупрямые не достигают точек ни оси ординат, так как при х = 0 значение функции определено по другому соответствию.
3. Графический способ. Здесь соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях с употреблением самопишущих приборов (осциллографы, сейсмографы и т.п.).
Область определения функции
Остановимся на процедуре нахождения области определения функции.
1. В том случае, когда функция задана в аналитическом виде (посредством формулы)
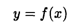 (3.1)
(3.1)
и никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу f в (3.1). Эти ограничения хорошо известны: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком логарифма должно быть только
положительным, а также некоторые другие. Приведем здесь два примера.
Пример 1.у = log2 (x2 — 5x + 6).
Область определения этой функции находится из условия x2 — 5x + 6 > 0. Поскольку x = 2 и x = 3 — корни квадратного трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-  , 2) и (3,
, 2) и (3,  ). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.
). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.
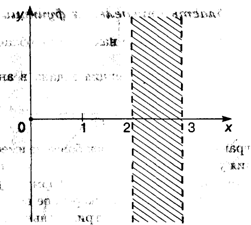
Рис. 3.4
Пример 2. у = arcsin 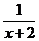 .
.
Область определения этой функции находится из совокупности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не должен равняться нулю, т.е.
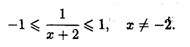
Двойное неравенство эквивалентно двум более простым неравенствам: х + 2 ≥ 1 и х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных промежутков: (-  , -3] и (-1,
, -3] и (-1,  ). Запретная точка х = -2 сюда не попадает. В отличие от предыдущего примера концы полуинтерваловвходят в область определения функции.
). Запретная точка х = -2 сюда не попадает. В отличие от предыдущего примера концы полуинтерваловвходят в область определения функции.
2. Область определения функции задана вместе с функцией f(x).
Пример 3. у = 3x-4/3 + 2, 1 ≤ х ≤ 4.
3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физическим смыслом).
Определение 2. Функция у = f(x) называется четной (симметрия относительно оси Оу), если для любых значений аргумента из области ее определения выполнено равенство
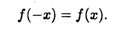
Определение 3. Функция у = f(x) называется нечетной (симметрия относительно начала координат О), если выполнено условие:
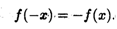
Например, функции у = х2 и у = cos x являются четными, а функции у = x3 и у = sin x— нечетными.
Приложения в экономике
Приведем примеры использования функций в области экономики.
1. Кривые спроса и предложения. Точка равновесия. Рассмотрим зависимости спроса D (demand) и предложения S (supply) от цены на товар Р (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от Р имеет вид ниспадающей кривой (рис. 3.5, а):
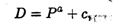 (3.2)
(3.2)
где а < 0. В свою очередь предложение растет с увеличением цены на товар, и потому зависимость S от Р имеет следующую характерную форму:
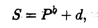 (3.3)
(3.3)
где b ≥ 1 (рис. 3.5, б). В формулах (3.2) и (3.3) с и d — так называемые экзогенные величины; они зависят от внешних причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (3.2) и (3.3), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.
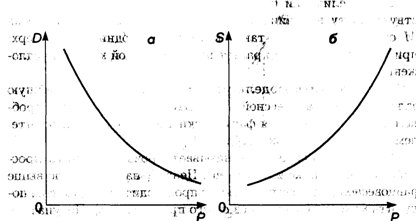
Рис. 3.5
Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие дается уравнением

и соответствует точке пересечения кривых D и S — это так называемая точка равновесия (рис. 3.6). Цена Ро, при которой выполнено условие (3.4), называется равновесной.
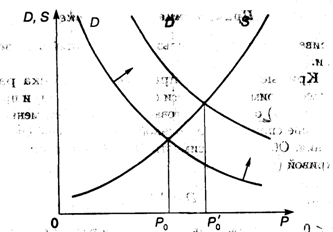
Рис. 3.6
При увеличении благосостояния населения, что соответствует росту величины с в формуле (3.2), точка равновесия М смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предложения S.
2. Паутинная модель рынка. Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проблем рынка, означающая фактически торг между производителем и покупателем (рис. 3.7).
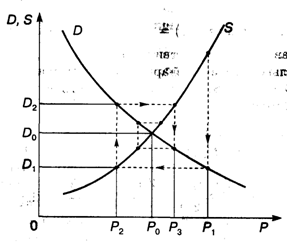
Рис. 3.7
Пусть сначала цену P1 называет производитель (в простейшей схеме он же и продавец). Цена P1 на самом деле выше равновесной (естественно, всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спрос D1 при этой цене и определяет свою цену Р2, при которой этот спрос D1 равен предложению. Цена Р2 ниже равновесной (всякий покупатель стремится купить подешевле). В свою очередь производитель оценивает спрос D2, соответствующий цене P2, и определяет свою цену Р3, при которой спрос равен предложению; эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к "скручиванию" спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену Р0:  Pn = P0.
Pn = P0.
Предел функции
Предел функции в точке
Пусть функция f(x) определена на некотором множестве X. Возьмем из Х последовательность точек
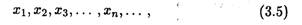
сходящуюся к точке а, причем а 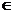 Х или a
Х или a 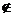 X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
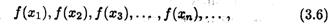
и правомерно рассмотреть вопрос о ее сходимости.
Определение. Число А называется пределом функции f(x) в точке а (или пределом функции при х  а), если для любой cходящейся к а последовательности (3.5) значений аргумента х, отличных от а, соответствующая последовательность значений функции (3.6) сходится к числу А.
а), если для любой cходящейся к а последовательности (3.5) значений аргумента х, отличных от а, соответствующая последовательность значений функции (3.6) сходится к числу А.
Для обозначения предельного значения функции используется следующая символика: 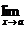 f(x)
f(x)  А. Заметим, что функция f(x) может иметь в точке а только одно предельное значение, поскольку последовательность f(xn) имеет только один предел.
А. Заметим, что функция f(x) может иметь в точке а только одно предельное значение, поскольку последовательность f(xn) имеет только один предел.
Приведем несколько примеров.
Пример 1. Функция f(x) = С = const имеет предел в каждой точке числовой прямой. Действительно, любой последовательности (3.5), сходящейся к точке а, соответствует последовательность (3.6), состоящая из одного и того же числа C, откуда следует, что f(xn)  С при n
С при n 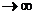 .
.
Пример 2. Функция f(x) = х в любой точке а числовой прямой имеет предел, равный а. Действительно, последовательности значений аргумента (3.5) и значений функции (3.6) в этом случае тождественны, и если последовательность {xn} сходится к а, то и последовательность {f(xn)} также сходится к а.
Пример 3. Функция f(x) = 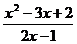 имеет в точке x = 0 предел, равный -2. Действительно, пусть {xn} — любая последовательность значений аргумента, сходящаяся к нулю, т.е. lim xп = 0 при n
имеет в точке x = 0 предел, равный -2. Действительно, пусть {xn} — любая последовательность значений аргумента, сходящаяся к нулю, т.е. lim xп = 0 при n 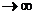 , тогда в силу свойств последовательностей 1—9 имеем
, тогда в силу свойств последовательностей 1—9 имеем
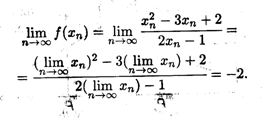
Левый и правый пределы функции
Здесь вводятся и в дальнейшем будут использоваться понятия односторонних пределов функции: когда последовательность значений аргумента xn  а либо слева от точки а (левый предел), либо справа (правый предел), т.е. либо xп < а, либо xп > а. Для правого (левого) предела функции используется символическая запись:
а либо слева от точки а (левый предел), либо справа (правый предел), т.е. либо xп < а, либо xп > а. Для правого (левого) предела функции используется символическая запись:
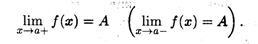
Пример 4. Рассмотрим функцию f(x) = sign x (п. 3.1, пример 3). В точке x = 0 эта функция имеет левый и правый пределы:
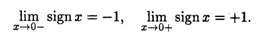
Действительно, для любой сходящейся к нулю последовательности {xn}, у которой все элементы xп < 0 (xn > 0), соответствующая последовательность значений функции состоит только из одного числа -1 (+1), т.е. предел слева (справа) в точке x = 0 также равен этому числу.
ТЕОРЕМА 1. Функция f(x) имеет в точке а предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. В таком случае предел функции равен односторонним пределам.
Предел функции при х 
 , x
, x  -
-  , х
, х 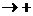

Кроме понятия предела функции в точке существует также и понятие предела функции при стремлении аргумента к бесконечности. Для обозначения предела функции при x 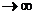 используется запись:
используется запись: 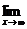 f(x) = А.
f(x) = А.
Приведем пример предела функции при х 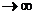 . Пусть f(x) = 1/x. Эта функция имеет предел при x
. Пусть f(x) = 1/x. Эта функция имеет предел при x 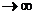 , равный нулю. Действительно, если (3.5) — бесконечно большая последовательность значений аргумента, то соответствующая последовательность (3.6) значений функции имеет вид 1/x1, 1/x2,..., 1/xn,...; она является бесконечно малой (п. 2.1), т. е. ее предел равен нулю, или в символической записи
, равный нулю. Действительно, если (3.5) — бесконечно большая последовательность значений аргумента, то соответствующая последовательность (3.6) значений функции имеет вид 1/x1, 1/x2,..., 1/xn,...; она является бесконечно малой (п. 2.1), т. е. ее предел равен нулю, или в символической записи 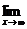 (1/x) = 0.
(1/x) = 0.
Аналогично можно доказать, что 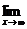 (1/xn) = 0 при п > 0.
(1/xn) = 0 при п > 0.
Теоремы о пределах функций
Арифметические операции над функциями, имеющими предел в точке а, приводят к функциям, также имеющим предел в этой точке.
ТЕОРЕМА 2. Пусть функции f(x) и g(х) имеют в точке а пределы А и В. Тогда функции f(x) ± g{x), f(x)g(x) и f(x)/g(x) (при В ≠ 0) имеют в точке а пределы, равные соответственно А± В, А В и А/В.
ТЕОРЕМА 3. Пусть функции f(x), g(x) и h(x) определены в некоторой окрестности точки а за исключением, быть может, самой точки а, и функции f(x) и g(х), имеют в этой точке предел, равный А: 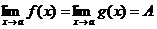 Кроме того, пусть выполнены неравенства f(x) ≤ h(x) ≤ g(x). Тогда
Кроме того, пусть выполнены неравенства f(x) ≤ h(x) ≤ g(x). Тогда
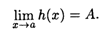
Заметим, что теоремы 3.2 и 3.3 справедливы и в случае, когда а является  , +
, +  или -
или -  .
.
Часто встречаются случаи, когда непосредственно применить теорему о пределе частного нельзя. Это так называемые неопределенности вида 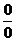 или
или 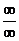 . Далее будет рассмотрен метод раскрытия этих неопределенностей, связанный с дифференцированием. Однако зачастую решение связано с более простыми методами: разложением числителя и знаменателя на сомножители, делением числителя и знаменателя на степеньx и т.д. Рассмотрим это на примерах.
. Далее будет рассмотрен метод раскрытия этих неопределенностей, связанный с дифференцированием. Однако зачастую решение связано с более простыми методами: разложением числителя и знаменателя на сомножители, делением числителя и знаменателя на степеньx и т.д. Рассмотрим это на примерах.
Пример 1. Найти предел 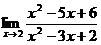 .
.
Решение. Нетрудно видеть, что непосредственная подстановка предельного значения x = 2 в дробь под знаком предела приводит к неопределенности вида 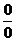 . Разложим квадратные трехчлены числителя и знаменателя на сомножители и сократим общий сомножитель, после чего уже подставим предельное значение х = 2:
. Разложим квадратные трехчлены числителя и знаменателя на сомножители и сократим общий сомножитель, после чего уже подставим предельное значение х = 2:
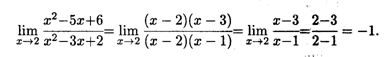
Пример 2. Найти предел 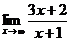 .
.
Решение. В задачах такого типа следует разделить числитель и знаменатель на старшую степень x (в данном случае это просто x) и затем применить теорему 3.2 о переходе к пределу в числителе и знаменателе с последующим переходом к пределу слагаемых. Имеем
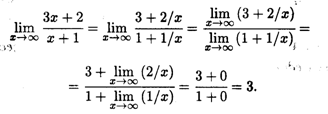
Пример 3. Найти предел 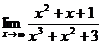 .
.
Решение. Поделим числитель и знаменатель дроби под знаком предела на x3 (это старшая степень x), после чего воспользуемся теоремой 3.2:
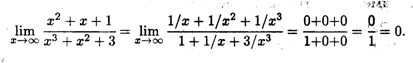
Поясним также раскрытие неопределенности вида  —
—  . Рассмотрим характерный случай.
. Рассмотрим характерный случай.
Пример 4. Найти предел 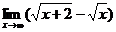 .
.
Решение. Здесь следует умножить и разделить выражение под знаком предела на сопряженное выражение — в данном случае на ( 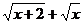 ), после чего воспользоваться приемом деления числителя и знаменателя на старшую степень x, в данном случае — на
), после чего воспользоваться приемом деления числителя и знаменателя на старшую степень x, в данном случае — на 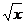 . Имеем
. Имеем
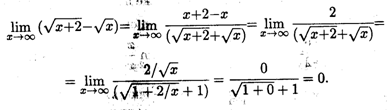
Два замечательных предела
В этом разделе приводятся два предела функции, которые наиболее широко используются в математике и ее приложениях. Доказательства соответствующих теорем мы опускаем.
ТЕОРЕМА 4. Предел функции 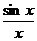 в точке х =0 существует и равен единице, т.е.
в точке х =0 существует и равен единице, т.е.

Предел (3.7) называется первым замечательным пределом. Этот предел применяется при вычислении ряда других пределов. Рассмотрим несколько примеров на применение предела (3.7).
Пример 1. Найти предел функции sin (ax) / bx при х  0.
0.
Решение. Преобразуем данную дробь так, чтобы в знаменателе был аргумент синуса; только тогда можно будет применить первый замечательный предел, поскольку при х  0 пределом ах также является нуль. Получаем
0 пределом ах также является нуль. Получаем
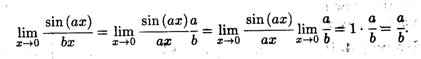
Пример 2. Найти 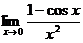 .
.
Решение. Теорему 3.2 здесь непосредственно применить нельзя, так как при х  0 знаменатель дроби стремится к нулю. Для решения задачи необходимо сначала преобразовать данную дробь, а затем уже выполнить предельный переход:
0 знаменатель дроби стремится к нулю. Для решения задачи необходимо сначала преобразовать данную дробь, а затем уже выполнить предельный переход:
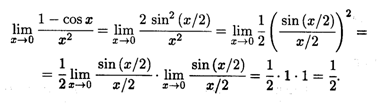
Пример 3. Найти 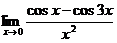 .
.
Решение. Как и в первых двух примерах, преобразуем данную дробь, чтобы "подогнать" ее под первый замечательный предел:

ТЕОРЕМА 5 (второй замечательный предел). Предел функции f(x) = 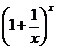 при х
при х
