На использование принципов умножения и сложения
Элементы комбинаторики
Комбинаторная математика занимается в основном задачами о существовании и подсчете различных комбинаций, которые можно составить из элементов заданного конечного множества. Эту область математики так назвал Готтфрид Вильгельм Лейбниц в 1666 году в своей диссертации об искусстве комбинаторики, в которой он решает основные комбинаторные задачи, приводящие к биномиальным коэффициентам и к факториалу. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке Паскаль, Ферма, Яков Бернулли и Эйлер, рассматривая азартные игры и всевозможные лотереи. В XVIII - XIX вв. в германских государствах Европы была предпринята попытка создать (Гинденбург, Штейнер, Эшенбах, Роте) комбинаторный анализ как единую науку, чему помешали громоздкость символического аппарата и слабость его оперативно-вычислительных возможностей.
В связи с развитием вычислительной техники резко расширились возможности перебора и повысился интерес к дискретным моделям, что обусловило новый подъем комбинаторной математики. Комбинаторные методы применяются сейчас в теории кодирования, планировании эксперимента, топологии, математической логике, теории игр, кристаллографии, биологии, статистической физике, экономике и т.д.
В нашем случае комбинаторика является основой для изучения теории вероятностей и математической статистики.
1.1. Опорная таблица


1.2. Методы

1.3. Алгоритмы

Графы
Начало теории графов было положено Эйлером в 1736 году в его знаменитой задаче о кёнигсбергских мостах. Исследования электрических цепей, моделей кристаллов и структур молекул, развитие формальной логики побудили к изучению графов. Большое число популярных головоломок поддавалось формулировкам непосредственно в терминах графов. Проблема четырех красок - наиболее известная среди таких задач - была поставлена Де Морганом в 1850 году. В ХХ столетии теория графов получила дальнейшее развитие, которое связано с новыми ее приложениями: в теории игр и программировании, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем биологии и психологии.
В данной работе графы являются основой для иллюстрации основных результатов в теории вероятностей, что позволяет сделать рассматриваемый материал более наглядным и доступным.
Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Это отношение удовлетворяет единственному требованию (аксиоме) - любое ребро инцидентно не более чем двум вершинам.
Пример 16.Построить граф, вершинами которого является множество {2, 3, 4, 5, 6}, а инцидентность задается наличием у указанных цифр делителей, отличных от единицы.
Решение. Взятые цифры обозначим на рисунке кружками, которые соединим отрезками (либо петлями) при наличии общих делителей.

Рис. 1
Этот граф содержит 5 петель - ребра, соединяющие (инцидентные) вершину саму с собой. Вершина "5" - изолированная, а подграф с вершинами {2, 3, 4, 6} является связным. Граф связный, если из любой вершины в любую другую можно "пройти" по ребрам. Циклом называется замкнутый путь из ребер, например, вершины {2, 4, 6} с соединяющими их попарно ребрами. Степенью вершины называется число ребер графа, инцидентных этой вершине.
Пример 17. Сколько различных обедов П.И. Чичиков мог насчитать из блюд, выставленных на столе у П.П. Петуха, если бы на каждый обед выбирать только одно холодное блюдо, одно первое блюдо и одно второе блюдо? На столе у П.П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра, свежепросоленная белужина; на первое - уха из стерлядей, щи с грибами; на второе - осетрина жареная, теленок, жаренный на вертеле.
Решение. Каждое блюдо изобразим кружком с первой буквой названия блюда, а соответствие блюд одного обеда - отрезками, соединяющими кружки. Возникает схема (граф), изображенный на рисунке:

Рис. 2
Граф помогает сосчитать число возможностей, их оказалось 12. Он же помогает узнать, сколько различных обедов можно составить, например, с икрой.
Математики, обратив внимание на сходство схемы на рисунке 2 с веткой дерева с листочками, назвали такие графы "деревьями".
Деревом называется связный граф без циклов. Очень важное понятие для нашего подхода к изложению теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания.
Пример 18.Поступающий на физмат должен сдать три вступительных экзамена по десятибалльной системе. Сколькими способами он может сдать экзамены, чтобы быть принятым в университет, если проходной балл в тот год составил 28 баллов?
Решение.Для решения этой задачи, как и во многих других комбинаторных и вероятностных задачах, эффективным оказывается организация элементов анализируемого множества в виде дерева. От одной выделенной вершины проводятся ребра, соответствующие оценке на первом экзамене, а затем к их концам добавляются новые ребра, соответствующие возможным результатам второго экзамена, а затем и третьего.

Рис. 3
Таким образом, для поступления на физмат можно сдать вступительные экзамены 10 различными способами.
Из этого представления можно извлечь ряд идей, плодотворных для изучения комбинаторики и вероятности.
При рассмотрении цепей Маркова (далее §11) нам потребуются графы, на ребрах которых поставлены стрелки, указывающие на переход из одного состояния в другое. Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую - концом. Граф, все ребра которого ориентированы, называется ориентированным графом.
Пример 19. Турнир по волейболу проводится по круговой системе между  командами. Докажите, что если какие-нибудь две команды одержали в турнире одинаковое число побед, то найдутся среди участников три команды I, II и III такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
командами. Докажите, что если какие-нибудь две команды одержали в турнире одинаковое число побед, то найдутся среди участников три команды I, II и III такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
Решение. Пусть 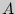 и
и 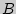 - две команды, одержавшие одинаковое число побед, например,
- две команды, одержавшие одинаковое число побед, например,  побед. Пусть к тому же
побед. Пусть к тому же 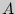 выиграла у
выиграла у 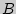 . Те
. Те  команд, у которых выиграла команда
команд, у которых выиграла команда 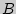 , обозначим
, обозначим  ,
,  , ...,
, ...,  (рис. 4).
(рис. 4).

Рис. 4
Команда 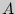 не могла одержать победы над всеми командами
не могла одержать победы над всеми командами  ,
,  , ...,
, ...,  , т.к. иначе она одержала бы больше чем
, т.к. иначе она одержала бы больше чем  побед (одна победа над
побед (одна победа над 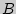 уже имеется). Следовательно, среди команд
уже имеется). Следовательно, среди команд  ,
,  , ...,
, ...,  найдется хотя бы одна, которая одержала победу над
найдется хотя бы одна, которая одержала победу над 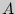 .
.
Из этого примера следует один из результатов теории графов о существовании ориентированных циклов в полном ориентированном графе.
Граф будет называться вероятностным, если рядом с каждым его ребром запишем соответствующую вероятность.
Пример 20.Построить вероятностное дерево исходов двух подбрасываний монеты на твердую поверхность.
Решение. Поскольку каждое подбрасывание монеты может закончиться одним из двух исходов, а именно, выпадением "герба" или "решки", то вероятностное дерево выглядит следующим образом:

ЗАДАЧА № 1
Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые начинаются цифрой 3?
РЕШЕНИЕ
1) Поставим цифру 3 на первое место и зафиксируем ее. А остальные четыре цифры будем переставлять для получения различных чисел. Таким образом, количество чисел будет определяться количеством перестановок среди чисел 1, 2, 4, 5. Чтобы его найти, воспользуемся формулой комбинаторики:
N = n! ,
где N – количество вариантов перестановок,
n – количество цифр.
N = 4! = 24.
ОТВЕТ: Из цифр 1, 2, 3, 4, 5 можно составить 24 пятизначных числа без повторения цифр, которые начинаются цифрой 3?
ЗАДАЧА № 2
Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.
РЕШЕНИЕ
Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.
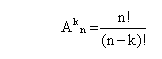
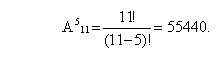
ОТВЕТ: При данных условиях можно составить 55440 различных расписаний.
ЗАДАЧА № 3
Сколькими способами можно выбрать 3 дежурных из группы в 20 человек?
РЕШЕНИЕ
Так как для данной задачи несущественен порядок выбора, то воспользуемся формулой комбинаторики для сочетания из 20 по 3:
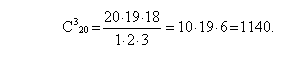
ЗАДАЧА № 1
Вычислить вероятность того, что некоторое событие не произойдет, если известно, что при n испытаниях оно в среднем происходит в m случаях.
РЕШЕНИЕ
1) Обозначим событие А = «Событие произошло». Определим вероятность появления данного события. Для этого воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:
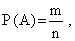
где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим вероятность того, что событие А не произойдет, по формуле:
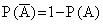
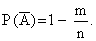
ОТВЕТ: Вероятность того, что событие не произойдет, равна 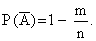
ЗАДАЧА №2
Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?
РЕШЕНИЕ
1) Обозначим событие А = «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:
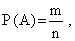
где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:
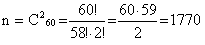
3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:
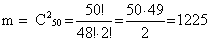
4) Определим вероятность события А:
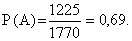
ОТВЕТ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены.
ЗАДАЧА № 3
Какова вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти?
РЕШЕНИЕ
1) Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:
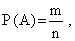
где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим n. Для этого воспользуемся формулой сочетания по 4 из 52(так как нас не интересует порядок вытянутых карт):
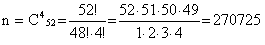
3) Обозначим событие А = «Из 4 вынутых карт 2 принадлежат пиковой масти». Найдем вероятность вытягивания 2 пиковых карт по формуле сочетания по 2 из 13 (так как всего карт пиковой масти 13):
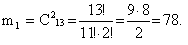
4) Найдем вероятность вытягивания оставшихся двух карт не пиковой масти по формуле сочетания по 2 из 39 (52-13).
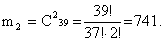
5) Полученные значения мы перемножаем: m = m1 ∙ m2
m = 78 ∙ 741 = 57798
6) Найдем вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти:
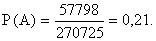
ОТВЕТ: Вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти, равна 0,21.
ЗАДАЧА № 1
Один из мальчиков родился в марте, а другой в апреле. Какова вероятность того, что оба они родились в первой неделе месяца?
РЕШЕНИЕ
1) Вероятность того, что первый мальчик родился в первой неделе марта равна:
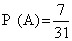
2) Вероятность того, что второй мальчик родился в первой неделе апреля равна:
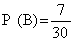
3) Вероятность того, что оба они родились в первой неделе месяца, равна P(A) ∙ P(B):
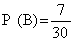
ОТВЕТ: Вероятность того, что оба мальчика родились в первой неделе месяца равна 0,05.
ЗАДАЧА №2
Для разрушения моста достаточно попадания одной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно 0,3; 0,4; 0,6; 0,7.
РЕШЕНИЕ
Для определения вероятности воспользуемся формулой вероятности появления хотя бы одного из n событий:
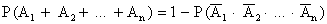
Обозначим события: А1 = «Первая бомба попала на мост»
А2 = «Вторая бомба попала на мост»
А3 = «Третья бомба попала на мост»
А4 = «Четвертая бомба попала на мост»
В нашем случае:
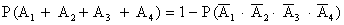
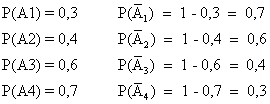
Тогда P (A1 + A2 + A3 + A4) = 1 – 0,7 ∙ 0,6 ∙ 0,4 ∙ 0,3 = 0,9496.
ОТВЕТ: Вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с заданными вероятностями попадания, равна 0,9496, то есть это достаточно достоверное событие.
ЗАДАЧА № 3
Чему равна вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях?
РЕШЕНИЕ
Обозначим события: А = «2 очка выпали на первой кости»
В = «2 очка выпали на второй кости»
С = «2 очка выпали на третьей кости»
Искомое событие X описывается следующей комбинацией:
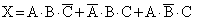
Так как события А, В и С несовместные и независимые, то вероятность события Х определяется по формуле:
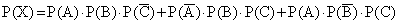
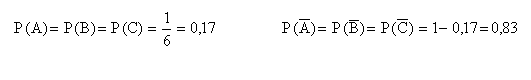
ЗАДАЧА № 1
Один из мальчиков родился в марте, а другой в апреле. Какова вероятность того, что оба они родились в первой неделе месяца?
РЕШЕНИЕ
1) Вероятность того, что первый мальчик родился в первой неделе марта равна:
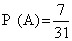
2) Вероятность того, что второй мальчик родился в первой неделе апреля равна:
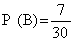
3) Вероятность того, что оба они родились в первой неделе месяца, равна P(A) ∙ P(B):
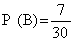
ОТВЕТ: Вероятность того, что оба мальчика родились в первой неделе месяца равна 0,05.
ЗАДАЧА №2
Для разрушения моста достаточно попадания одной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно 0,3; 0,4; 0,6; 0,7.
РЕШЕНИЕ
Для определения вероятности воспользуемся формулой вероятности появления хотя бы одного из n событий:
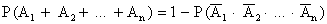
Обозначим события: А1 = «Первая бомба попала на мост»
А2 = «Вторая бомба попала на мост»
А3 = «Третья бомба попала на мост»
А4 = «Четвертая бомба попала на мост»
В нашем случае:
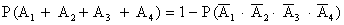
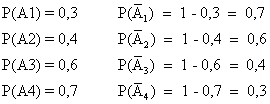
Тогда P (A1 + A2 + A3 + A4) = 1 – 0,7 ∙ 0,6 ∙ 0,4 ∙ 0,3 = 0,9496.
ОТВЕТ: Вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с заданными вероятностями попадания, равна 0,9496, то есть это достаточно достоверное событие.
ЗАДАЧА № 3
Чему равна вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях?
РЕШЕНИЕ
Обозначим события: А = «2 очка выпали на первой кости»
В = «2 очка выпали на второй кости»
С = «2 очка выпали на третьей кости»
Искомое событие X описывается следующей комбинацией:
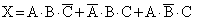
Так как события А, В и С несовместные и независимые, то вероятность события Х определяется по формуле:
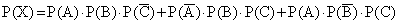
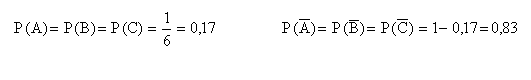
Пример 6. Сколько существует двузначных чисел?
Решение. Поскольку в двузначном числе цифра, обозначающая число десятков, должна быть отлична от нуля, то 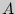 = {1, 2, ..., 9},
= {1, 2, ..., 9}, 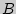 = {0, 1, 2, ..., 9} и
= {0, 1, 2, ..., 9} и 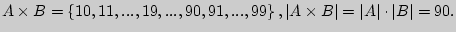
Элементы комбинаторики
Комбинаторная математика занимается в основном задачами о существовании и подсчете различных комбинаций, которые можно составить из элементов заданного конечного множества. Эту область математики так назвал Готтфрид Вильгельм Лейбниц в 1666 году в своей диссертации об искусстве комбинаторики, в которой он решает основные комбинаторные задачи, приводящие к биномиальным коэффициентам и к факториалу. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке Паскаль, Ферма, Яков Бернулли и Эйлер, рассматривая азартные игры и всевозможные лотереи. В XVIII - XIX вв. в германских государствах Европы была предпринята попытка создать (Гинденбург, Штейнер, Эшенбах, Роте) комбинаторный анализ как единую науку, чему помешали громоздкость символического аппарата и слабость его оперативно-вычислительных возможностей.
В связи с развитием вычислительной техники резко расширились возможности перебора и повысился интерес к дискретным моделям, что обусловило новый подъем комбинаторной математики. Комбинаторные методы применяются сейчас в теории кодирования, планировании эксперимента, топологии, математической логике, теории игр, кристаллографии, биологии, статистической физике, экономике и т.д.
В нашем случае комбинаторика является основой для изучения теории вероятностей и математической статистики.
1.1. Опорная таблица


1.2. Методы

1.3. Алгоритмы

Графы
Начало теории графов было положено Эйлером в 1736 году в его знаменитой задаче о кёнигсбергских мостах. Исследования электрических цепей, моделей кристаллов и структур молекул, развитие формальной логики побудили к изучению графов. Большое число популярных головоломок поддавалось формулировкам непосредственно в терминах графов. Проблема четырех красок - наиболее известная среди таких задач - была поставлена Де Морганом в 1850 году. В ХХ столетии теория графов получила дальнейшее развитие, которое связано с новыми ее приложениями: в теории игр и программировании, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем биологии и психологии.
В данной работе графы являются основой для иллюстрации основных результатов в теории вероятностей, что позволяет сделать рассматриваемый материал более наглядным и доступным.
Графом называется два множества с отношением инцидентности между их элементами, называемыми вершинами и ребрами. Это отношение удовлетворяет единственному требованию (аксиоме) - любое ребро инцидентно не более чем двум вершинам.
Пример 16.Построить граф, вершинами которого является множество {2, 3, 4, 5, 6}, а инцидентность задается наличием у указанных цифр делителей, отличных от единицы.
Решение. Взятые цифры обозначим на рисунке кружками, которые соединим отрезками (либо петлями) при наличии общих делителей.

Рис. 1
Этот граф содержит 5 петель - ребра, соединяющие (инцидентные) вершину саму с собой. Вершина "5" - изолированная, а подграф с вершинами {2, 3, 4, 6} является связным. Граф связный, если из любой вершины в любую другую можно "пройти" по ребрам. Циклом называется замкнутый путь из ребер, например, вершины {2, 4, 6} с соединяющими их попарно ребрами. Степенью вершины называется число ребер графа, инцидентных этой вершине.
Пример 17. Сколько различных обедов П.И. Чичиков мог насчитать из блюд, выставленных на столе у П.П. Петуха, если бы на каждый обед выбирать только одно холодное блюдо, одно первое блюдо и одно второе блюдо? На столе у П.П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра, свежепросоленная белужина; на первое - уха из стерлядей, щи с грибами; на второе - осетрина жареная, теленок, жаренный на вертеле.
Решение. Каждое блюдо изобразим кружком с первой буквой названия блюда, а соответствие блюд одного обеда - отрезками, соединяющими кружки. Возникает схема (граф), изображенный на рисунке:

Рис. 2
Граф помогает сосчитать число возможностей, их оказалось 12. Он же помогает узнать, сколько различных обедов можно составить, например, с икрой.
Математики, обратив внимание на сходство схемы на рисунке 2 с веткой дерева с листочками, назвали такие графы "деревьями".
Деревом называется связный граф без циклов. Очень важное понятие для нашего подхода к изложению теории вероятностей. При помощи дерева удобно изображать исходы того или иного испытания.
Пример 18.Поступающий на физмат должен сдать три вступительных экзамена по десятибалльной системе. Сколькими способами он может сдать экзамены, чтобы быть принятым в университет, если проходной балл в тот год составил 28 баллов?
Решение.Для решения этой задачи, как и во многих других комбинаторных и вероятностных задачах, эффективным оказывается организация элементов анализируемого множества в виде дерева. От одной выделенной вершины проводятся ребра, соответствующие оценке на первом экзамене, а затем к их концам добавляются новые ребра, соответствующие возможным результатам второго экзамена, а затем и третьего.

Рис. 3
Таким образом, для поступления на физмат можно сдать вступительные экзамены 10 различными способами.
Из этого представления можно извлечь ряд идей, плодотворных для изучения комбинаторики и вероятности.
При рассмотрении цепей Маркова (далее §11) нам потребуются графы, на ребрах которых поставлены стрелки, указывающие на переход из одного состояния в другое. Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую - концом. Граф, все ребра которого ориентированы, называется ориентированным графом.
Пример 19. Турнир по волейболу проводится по круговой системе между  командами. Докажите, что если какие-нибудь две команды одержали в турнире одинаковое число побед, то найдутся среди участников три команды I, II и III такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
командами. Докажите, что если какие-нибудь две команды одержали в турнире одинаковое число побед, то найдутся среди участников три команды I, II и III такие, что I выиграла у II, II выиграла у III, a III выиграла у I.
Решение. Пусть 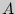 и
и 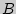 - две команды, одержавшие одинаковое число побед, например,
- две команды, одержавшие одинаковое число побед, например,  побед. Пусть к тому же
побед. Пусть к тому же 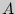 выиграла у
выиграла у 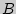 . Те
. Те  команд, у которых выиграла команда
команд, у которых выиграла команда 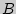 , обозначим
, обозначим  ,
,  , ...,
, ...,  (рис. 4).
(рис. 4).

Рис. 4
Команда 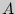 не могла одержать победы над всеми командами
не могла одержать победы над всеми командами  ,
,  , ...,
, ...,  , т.к. иначе она одержала бы больше чем
, т.к. иначе она одержала бы больше чем  побед (одна победа над
побед (одна победа над 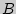 уже имеется). Следовательно, среди команд
уже имеется). Следовательно, среди команд  ,
,  , ...,
, ...,  найдется хотя бы одна, которая одержала победу над
найдется хотя бы одна, которая одержала победу над 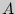 .
.
Из этого примера следует один из результатов теории графов о существовании ориентированных циклов в полном ориентированном графе.
Граф будет называться вероятностным, если рядом с каждым его ребром запишем соответствующую вероятность.
Пример 20.Построить вероятностное дерево исходов двух подбрасываний монеты на твердую поверхность.
Решение. Поскольку каждое подбрасывание монеты может закончиться одним из двух исходов, а именно, выпадением "герба" или "решки", то вероятностное дерево выглядит следующим образом:

На использование принципов умножения и сложения
1.Сколькими способами могут восемь человек стать в очередь к театральной кассе?
Решение задачи:
Существует 8 мест, которые должны занять 8 человек. На первое место может стать любой из 8 человек, т.е. способов занять первое место – 8. После того, как один человек стал на первое место, осталось 7 мест и 7 человек, которые могут быть на них размещены, т.е. способов занять второе место – семь. Аналогично для третьего, четвертого и т.д. места. Используя принцип умножения, получаем произведение –  . Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8.
. Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8.
Ответ: P8 = 8!
2.Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?
Решение задачи:
В современном латинском алфавите 26 букв. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место.
1) На оставшиеся два места может претендовать любая из 26-ти букв, т.к. буквы в позывных могут повторяться. Используя принцип умножения, получаем произведение: 1  = 262.
= 262.
2) На второе место можно поставить любую из 25 букв, т.к. в позывных буквы не должны повторяться. На третье место – 24 буквы, на четвертое место – 23 буквы. Используя принцип умножения, получаем произведение: 1  .
.
Ответ: 1) 262; 2)  .
.
3.В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?
Решение задачи:
Действие, которое должно быть выполнено особым способом, необходимо выполнять первым. Итак, на место водителя можно посадить только одного из трех человек (умеющего водить машину), т.е. существуют 3 способа занять первое место. Второе место может занять любой из 6 человек, оставшихся после того, как место водителя будет занято. И т.д. Используя принцип умножения, получаем произведение: 3  = 3
= 3 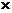 6! = 3
6! = 3 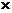 P6.
P6.
Ответ: 3 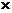 P6 = 3
P6 = 3 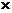 6!.
6!.
4.Алфавит некоторого языка содержит 30 букв. Сколько существует шестибуквенных слов (цепочка букв от пробела до пробела), составленных из букв этого алфавита, если:
1) буквы в словах не повторяются?
2) буквы в словах могут повторяться?
Решение задачи:
Существует шесть мест, на которые нужно разместить 30 букв.
1. Буквы не должны повторяться. Используя принцип умножения, получаем произведение:  . Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом:
. Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом: 
 1=
1= 
 =
=  =
=  =
=  = А
= А  ‑ формула для размещений.
‑ формула для размещений.
2. Буквы повторяются. Используя принцип умножения, получаем: 30 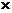 30
30 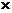 30
30 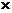 30
30 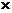 30
30 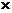 30 = 306 = Ã
30 = 306 = Ã  – формула для размещений с повторениями.
– формула для размещений с повторениями.
Ответ: 1) А  ; 2) Ã
; 2) Ã  .
.
5.Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?
Решение задачи:
Необходимо посчитать, сколько существует трехзначных, четырехзначных и пятизначных чисел, составленных из этих пяти цифр. Трехзначных чисел - 5 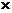 4
4 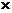 3 = А
3 = А  , четырехзначных – 5
, четырехзначных – 5 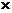 4
4 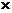 3
3 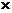 2 = А
2 = А  , пятизначных – 5
, пятизначных – 5 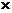 4
4 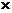 3
3 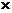 2
2 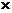 1 = А
1 = А  . Используем принцип сложения: А
. Используем принцип сложения: А  + А
+ А  + А
+ А  = 60 + 120 + 120 = 300.
= 60 + 120 + 120 = 300.
Ответ: 300.
