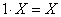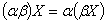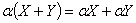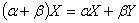Коммутативность сложения и умножения.

Определение.

Комплекснымчисломназываетсяупорядоченнаяпара(a;b) действительныхчиселaиb.Числа(a;b)и(c;d)называютсяравными,еслиa=cиb=d.Действительноечислоaназываетсядействительнойчастьючисла(a;b),адействительноечислоb-мнимойчастьючисла(a;b).Суммойкомплексныхчисел(a;b)и(c;d)называетсячисло(a+c;b+d),аихпроизведением-число(ac-bd;ad+bc).МножествовсехкомплексныхчиселобозначаетсячерезC.

Правила:

1)Комплексноечисло(0;1)называетсямнимойединицейиобозначаетсячерезi.

Поопределениюумножениякомплексныхчисел

i2=(0;1) ×(0;1)=(-1;0) , отсюда следует что i²=-1.

2)Заметим,что

(a;b)=(a;0)+(0;b)=(a;0)+(b;0)×(0;1)=a+bi

Выражениеa+biназываетсяалгебраическойформойкомплексногочисла (a; b).

3)Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

Операции над комплексными числами:

1) Правило сложения и вычитания комплексных чисел. Спримером.

(a+bi)+(c+di)=(a+c)+(b+d)i Пример : 1+i+3+7i=4+8i

Нулем комплексных чисел является : 0+0i=0 1+i+0+0i=1+i

2)Правилоумножения.

(a+bi)*(c+di)=(ac-bd)+(ad+bc)i Пример : (1+i)*(3-2c)=(3+2)*(-2+3)i=5+i

3)Правило деления.

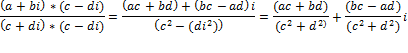
Операция деления не возможна, если c,d=0

Множество комплексных чисел является полем.

Коммутативность сложения и умножения.

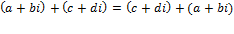
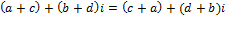
Умножения

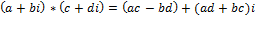
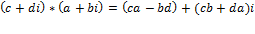
Ассоциативность

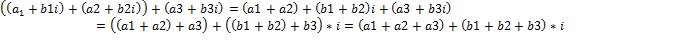
Если проссумируемвыражение расставив скобки иначе, то результат будет такой же.

Ассоциативность умножения.

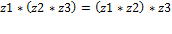
Z1=a1+b1i

Z2=a2+b2i

Z3=a3+b3i

4)Дистрибутивность умножения относительно сложения

z1(z2+z3)=z1*z2+z1*z3

5)Наличие нуля и единицы.

0+0i*(a+bi)= (0a-0b)+(0b+0a)i=0 – мультипротикативыйноль.

единицы :

(1+0i)*(a+bi)=(1*a-0b)+(1*b+0a)i=a+bi

Тригометрическая запись числа.

Любое число z=a+bi можно на плоскости изобразить точкой , с координатами (a;b) a – x , b – y .

Любое комплексное число имеет свой аргумент Arg(z) (между осью абцисс и вектором)

Так же любое комплексное число имеет норму |z|.

r=|z| - длина его вектора

r=|z|=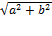

Любое комплексное число определяется своей нормой и аргументом, при этом 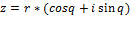– тригометрическая запись числа.

cosq= a/r , sinq = b/r

Модулем комплексного числа 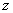называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Аргументом комплексного числа 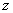называется угол 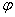между положительной полуосьюдействительной оси 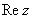и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

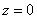Вопрос 2.Кольцо матриц над полем действительных чисел. Основные операции над матрицами. Свойства операций.

Матрицей называется прямоугольная таблица чисел.

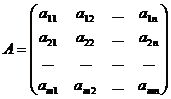
А – матрица, 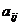- элемент матрицы, 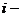номер строки, в которой стоит данный элемент, 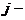номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Определение.Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида:

= E,

называетсяединичной матрицей.

Операции над матрицами:

Умножение матриц.

mxnи nxq, называется матрица размерности mxq.

Количество столбцов 1-ой матрицы должно совпадать с количеством строк 2-ой матрицы.

Умножение происходит таким образом, берется 1 строка 1-ой матрицы и умножается на 1 столбец 2-ой матрицы, далее 1 строка 1-ой матрицы умножается на 2 столбец 2-ой матрицы и т.д и получится 1 строка НОВОЙ МАТРИЦЫ.

Пример:

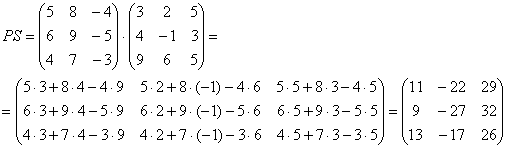
Свойства умножения матриц:

· 1.ассоциативность (AB)C = A(BC);

· 2.некоммутативность (в общем случае): AB 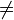BA;

· 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

· 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB)

Коммуникативность:

Умножение матриц не коммуникативно, и даже в том случае, когда матрицы квадратные все равно 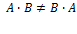, например имеется 2 матрицы 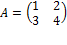и 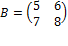результатом умножения матрицы А на матрицу Bбудет матрица 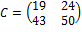, а если мы матрицу Bумножим на матрицу А получится 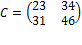. Множество квадратный матриц mxn замкнуто относительно умножения

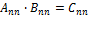. Множество матриц nxm обладают мультипликативной единицей ,

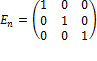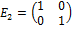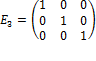, . Действительно, если перемножить матрицу 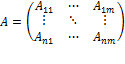и 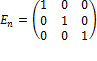, то получим =>

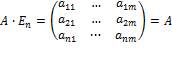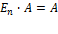
Ассоциативность:

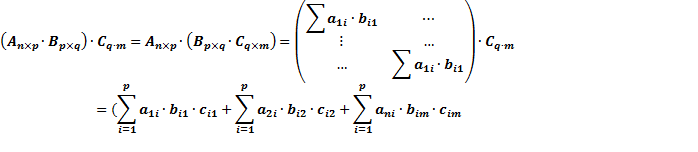
Вопрос 3. Определители. Теорема Лапласа. Свойства определителей.

Определитель– это число, которое считается по определенному правилу.

Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов.

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

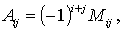
1)Определитель можно посчитать только у квадратной матрицы.

2) Определитель матрицы |An|=An

3)Определитель матрицы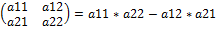

5) Для вычисления матрицы 3x3 существует правило треугольников (Правило Саррюса)

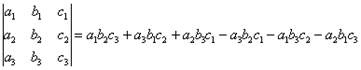
Если дана матрица 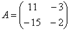, то ее определитель обозначают 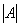. Также очень часто определитель обозначают латинской буквой 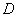или греческой .

Теорема.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Доказательство.

Пусть система совместна. Тогда существуют числа 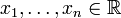такие, что 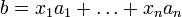. Следовательно, столбец 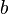является линейной комбинацией столбцов 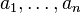матрицы 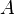. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

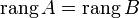Достаточность

Пусть 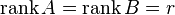. Возьмем в матрице 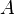какой-нибудь базисный минор. Так как 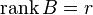, то он же и будет базисным минором и матрицы 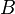. Тогда, согласно теореме о базисном миноре, последний столбец матрицы 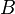будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 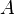. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

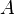Теорема о базисном миноре.

Теорема.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.

Метод Гауса.

Пусть имеется СЛУ:

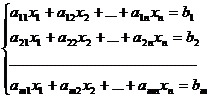
Доказательство.

1)Умножаем строку на число Альфа:

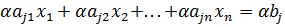, где 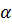(альфа) не равна нулю =>решение не меняется.

2)Сумма строк

+

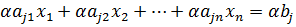
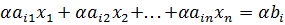
При сложении 2 строк с некоторым коэффициентом если ранее выполнялись тождества для отдельной строки, то и в сумме также будет выполняться равенства. При этом данное преобразование обратимо и не добавляет новых решений.

=>

=>

a a a

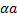b b+ b

+(-

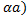
Из тождества aи bполучается b+ 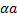, но из тождества а и b+ 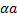можно получить тождества aи b.

Матричный метод.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений:

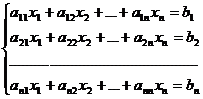
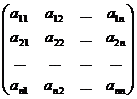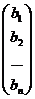Составим матрицы: A= ; B = ; X = .

Систему уравнений можно записать:A×X = B.

Сделаем следующее преобразование: A^-1×A×X = A^-1×B, т.к. А^-1×А = Е, тоЕ×Х = А^-1×В

Х = А^-1×В

Вопрос 8.Однородные СЛУ. Построение фундаментальной системы решений

Однородная Система Уравнений (ОСУ) – называется СЛУ , в которой свободные коэффициенты равны 0.

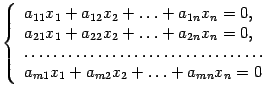
Однородная СЛУ всегда имеет хотя бы одно решение.

Найдем все решения ОСЛУ, методом Гаусса можно привести данную матрицу к треугольной.

Если ранг матрицы равен n, то элементарными преобразованиями из СЛУ можно получить равносильную ей вида:

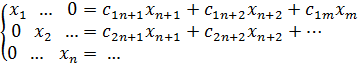
При этом любому набору 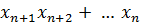можно сопоставить решение СЛУ

Любая линейная комбинация решений ОСЛУ является решением СЛУ.

Количество линейно независимых решений равно m-rangA, где m-число переменных;

если m=rangA, то Фундаментальной Системы Решений не существует.

ФСР: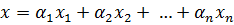

Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Вопрос 9. Векторы. Основные понятия. Скалярное произведение, его свойства

Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Определение.Длиной (модулем) вектора называется расстояние между началом и концом вектора.

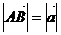
Определение.Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Определение.Векторы называются компланарными, если существует плоскость, которой они параллельны.

Определение.Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Определение.Линейными операциями над векторами называется сложение и умножение на число.

Суммой векторов является вектор -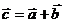

Произведение - 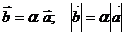, при этом коллинеарен .

Вектор сонаправлен с вектором ( ­­ ), если a> 0.

Вектор противоположно направлен с вектором ( ­¯ ), если a< 0.

Линейным пространством над полем 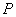(P- Это поле)называется множество 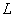, в котором введены операция сложения и операция умножения на числа из поля 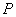. Причем, выполняются следующие аксиомы:

Аксиомы, определяющие операцию сложения.

1. 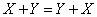, коммутативность

2. 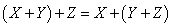, ассоциативность

3. 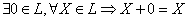, существование нулевого вектора

4. 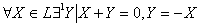(для любого вектора 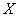из множества 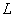существует единственный 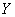такой, что ).

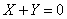Аксиомы, определяющие операцию умножения на числа.

1. 
2. 
3. 
4. 

Скалярным произведениемвекторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

× = ï ïï ïcosj

Свойства скалярного произведения:

Эллипс.

Определение.Эллипсом в каноническом виде наз-ся множество всех точек плоскости координаты которых удовлетворяют уравнению .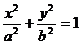

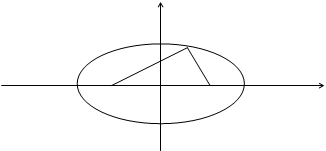
Определение.Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

M   М r1 r2 F1OF2

у

r1   М r1 r2 F1OF2

r2   М r1 r2 F1OF2

O   М r1 r2 F1OF2

x   М r1 r2 F1OF2

F2   М r1 r2 F1OF2

F1   М r1 r2 F1OF2

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема.Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

откуда c=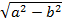

Определение.Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a.

Т.к. с<a, то е < 1.

Теорема.Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:

r₁ = a – ex, r₂ = a + ex.

Доказательство.Выше было показано, что r₁ + r₂ = 2a. Кроме того, из геометрических соображений можно записать:

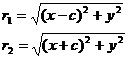
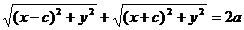
После возведения в квадрат и приведения подобных слагаемых:

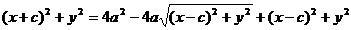
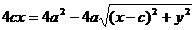
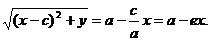
Аналогично доказывается, что r₂ = a + ex. Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.

Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

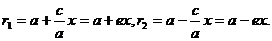Составим уравнения директрис:

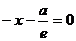(D₁), 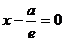(D₂). Тогда 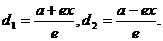Отсюда r_i/ d_i= e, что и требовалось доказать.

Теорема 2:

т. М принадлежит эллипсу 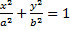не являющемуся окружностью, тогда и только тогда, когда отношение расстояния от М до фокуса к расстоянию от М до соответствующей этому фокусу директриссы равно эксцентриситету.

Доказательство:

Обозначим через l(L-малая) директриссу , расстояние от точки М (х,у) до данной директриссы равно 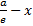, преобразуем 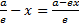, используя лемму получаем, что если точка М принадлежит эллипсу, то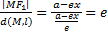

Достаточность пусть М(х,у) произвольная точка в плоскости, для которой выполняется:

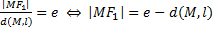по формулам длины отрезка: ,

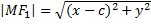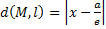возведем данное уравнение в квадрат:

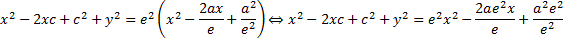
зная что ea=c, последнее равенство будет выглнядеть:

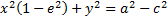, так как 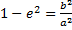, а 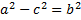в итоге получим:

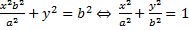таким образом точка М принадлежит эллипсу.

Вопрос 14. Кривые второго порядка.Каноническое уравнение параболы и гиперболы.

Гипербола.

Гиперболойназывается множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы: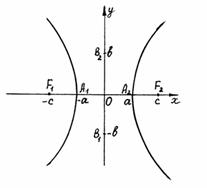

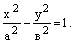Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых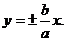

Определение.Отношение 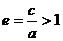называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а² = b²:

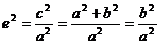
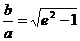
Если а = b, e = 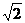, то гипербола называется равнобочной (равносторонней).

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .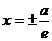

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (осьОх для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Эксцентриситет гиперболы e> 1.

3)Отношение расстояния r_iот точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Парабола.

Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки Fэтой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

y² = 2px ,Уравнение директрисы: x = -p/2.

называемомуканоническим уравнением параболы. Величина рназывается параметромпараболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является осьОх, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Вопрос 15. Классификация кривых 2-го порядка.Приведение к каноническому виду.

Цилиндрические поверхности.

Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

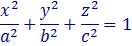
где a, b, c>0 — параметры эллипсоида. Это уравнение называется каноническим уравнением эллипсоида, а система координат, в которой эллипсоид описывается каноническим уравнением, называется канонической.

Из уравнения эллипсоида следует, что поверхность симметрична относительно координатных плоскостей, начало координат является центром эллипсоида.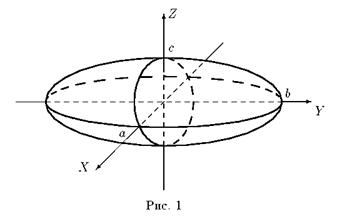

Исследуем форму эллипсоида с помощью метода сечений (рис.1).

Рассмотрим сечения эллипсоида плоскостями z = h , параллельными плоскости XOY (z=h):

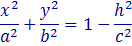
При | h |<c в сечении получается эллипсы с полуосями.

При h = ± c плоскость z = h касается эллипсоида в точках (0, 0, ± c) .

При | h |>c плоскость z = h не пересекает эллипсоид (в сечении — пустое множество).

Аналогично исследуется сечения по другим плоскостям XOZ(y=0),YOZ (x=0). Получится

y=0 : 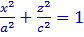и при x=0 :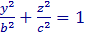

Любое сечение эллипса параллельное координатным плоскостям будет эллипс.

Гиперболоид.

Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

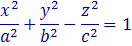
где a, b, c>0 — параметры гиперболоида. Это уравнение называется каноническим уравнением однополостного гиперболоида, а система координат, в которой гиперболоид описывается каноническим уравнением, называется канонической.

Исследуем форму однополостного гиперболоида с помощьюметода сечений (рис.1)

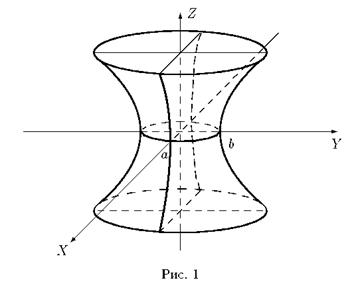
Рассмотрим сечения гиперболоида плоскостями z = h , параллельными плоскости XOY (z=h):

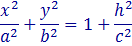
При любых значениях h в сечении получается эллипсы с полуосями.

Аналогично исследуются сечения гиперболоида плоскостями, параллельными координатным плоскостями XOZ (y=0) и YOZ (x=0). В частности,

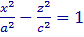– т. е. в сечении координатной плоскостью y = 0 получается гипербола, вершины которой лежат на оси OX , и 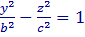т. е. в сечении координатной плоскостью x = 0 также получается гипербола, вершины которой лежат на оси OY

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

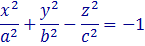
где a, b, c>0 — параметры гиперболоида. Это уравнение называется каноническим уравнением двуполотного гиперболоида, а система координат, в которой гиперболоид описывается каноническим уравнением, называется канонической.

Исследуем форму двуполостного гиперболоида с помощью метода сечений (рис.2).

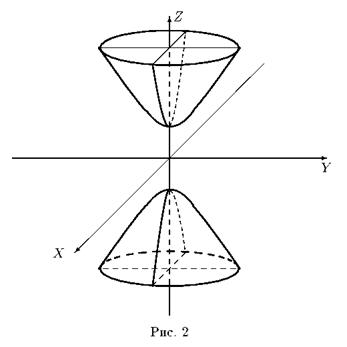
Рассмотрим сечения гиперболоида плоскостями z = h , параллельными плоскости XOY :

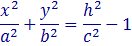
При | h |>c в сечении получается эллипсы с полуосями. При h =± c плоскость z = h касаетсягиперболоида в точках (0, 0, ± c) и, наконец, при | h |<c плоскость z = h не пересекает гиперболоида (в сечении — пустое множество)

Аналогично исследуются сечения гиперболоида плоскостями, параллельными координатным плоскостями XOZ и YOZ . В частности

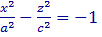т. е. в сечении координатной плоскостью y = 0 получается гипербола, вершины которой лежат на оси OZ , и 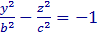т. е. в сечении координатной плоскостью x = 0 также получается гипербола, вершины которой лежат на оси OZ .

Вопрос 19. Метод сечений.Цилиндры и Конусы.(С примерами).

Конусом 2 –ого порядка называется поверхность, которая в некоторой декартовой системе координат определяется уравнением
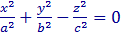где a, b, c>0 — параметры конуса.Это уравнение называется каноническим уравнением конуса, а система координат, в которой конус описывается каноническим уравнением, называется канонической.

Исследуем форму конуса с помощью метода сечений (рис. 1).

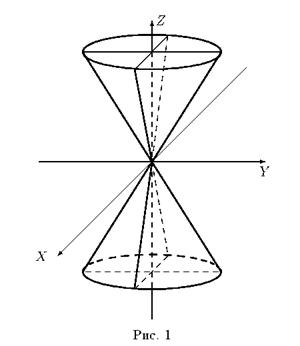
Рассмотрим сечения плоскостями z = h , параллельными плоскости XOY :

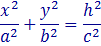
При любых значениях h ≠ 0 в сечении получается эллипсы с полуосямиПри h = 0 в сечении получается точка — начало координат.

Аналогично исследуются сечения конуса плоскостями, параллельными координатным плоскостями XOZ и YOZ . В частности,

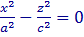т.е. в сечении координатной плоскостью y = 0 получается пара прямых, пересекающихся в начале координат. Аналогично 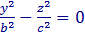т.е. в сечении координатной плоскостью x = 0 также получается пара прямых, пересекающихся в начале координат.

Цилиндр

Цилиндрической поверхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:

F(x, y) = 0, F(x, z) = 0 или F(y, z) = 0.

Примеры цилиндрических поверхностей 2–го порядка.

Эллиптический цилиндр.Уравнение

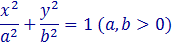
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1).

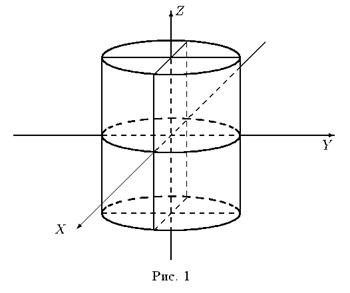
В частности, уравнение x² + y² = R² в трехмерном пространстве определяет круглый цилиндр.

Гиперболический цилиндр. Уравнение

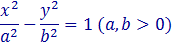
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2).

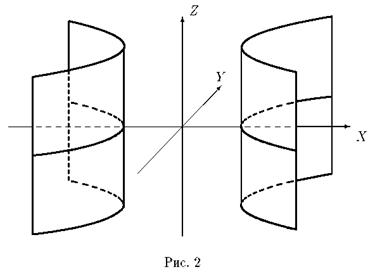
Параболический цилиндр. Уравнение

y2 = 2px ( p>0 )

в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является парабола (рис. 3).

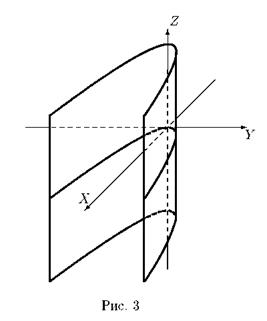
Вопрос 20. Линейные пространства.Основныепонятия.Теорема о Базисе.

Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + yиз L, называемый суммой x и y, причём:

x + y = y + x− сложение коммутативно;

x + (y + z) = (x + y) + z− сложение ассоциативно;

x +0= x − существует единственный нулевой элемент 0( x +0= x для любого x из L);

x + (− x)= 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0для любого x из L).

2. Каждой паре x и α, где α −число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.

Определение:Если в пространстве Lимеются векторы линейного преобразования 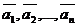, то другой вектор 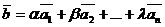является линейной комбинацией векторов .

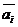Определение:Если 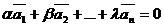только при a = b = … = l = 0, то векторы 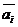называются линейно независимыми.

Определение:Если в линейном пространстве Lесть n линейно независимых векторов, но любые n + 1 векторов линейно зависимы, то пространство Lназывается n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L.

Утверждение: все максимально линейно независимые системы векторов имеют одинаковое количество векторов.

Доказательство (теорема о базисе):

Пусть есть 2-е линейно независимые системы векторов, с разным количеством векторов, тогда любой вектор линейного пространства выражается линейно через вектора этих систем.

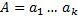
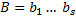
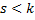
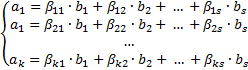, где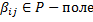

Система s-ок: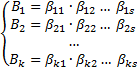

имеет векторов больше чем Sи поэтому линейно зависима, следовательно существует набор скаляров 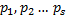для которого 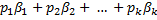равна нулю.

Домножим строчки 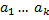на этот набор скаляров:

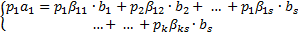слева положим линейную комбинацию системы векторов А, где не все коэффициенты равны нулю. А справа раскрыв скобки получим следующий коэффициент при :

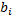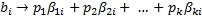
Это i-ая координата выбранной линейной комбинации векторов системы B и она равна нулю. Значит система векторовт А линейно зависима. Поэтому возникает противоречие.

Вопрос 21. Матрица перехода от Базиса к Базису.

L -n- мерное линейное пространство с базисом 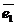, ,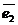…, 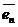. Другой базис задан векторами 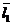, 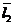.. . 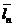Тогда они также являются векторами этого пространства и их можно представить в виде линейной комбинации векторов , ,…, :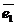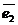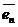