Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.

, .

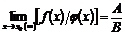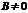5) Если 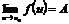, , 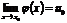то предел сложной функции

.

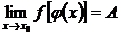6)Если в некоторой окрестности точки 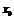(или при достаточно больших 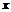) 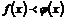, то

.

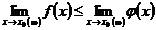Вопрос

Основные приемы вычисления пределов

Вопрос

Первый замечательный предел

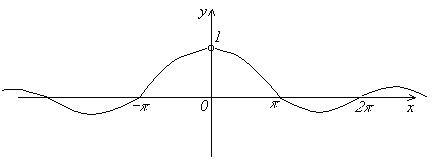
Функция 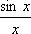не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.

Однако, можно найти предел этой функции при х→0.

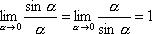
Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.

Вопрос

Второй замечательный предел

Определение. Числом 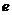(вторым замечательным пределом) называется предел числовой последовательности :

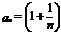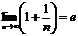, где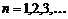

Прямым вычислением можно убедиться, что 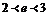, 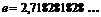(иррациональное число, число Эйлера).

Если рассмотреть функцию 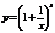, то при 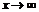функция имеет предел, равный числу :

.

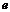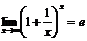Или если 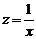, то .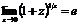

Непосредственное вычисление этого предела приводит к неопределенности 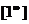. Однако доказано, что он равен числу 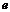. Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .

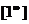Число 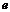(число Эйлера, неперово число) играет важную роль в математическом анализе. График функции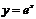

Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию 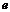, называемые натуральными. Натуральные логарифмы обозначаются символом .

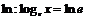Пример. .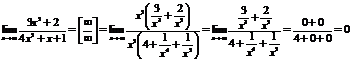

Пример. = .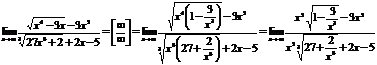

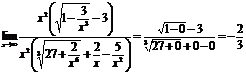Пример. .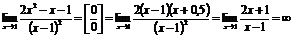

Пример.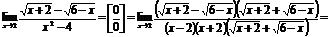

.

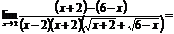
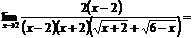
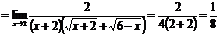Пример. .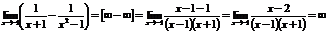

Пример. .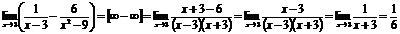

Пример. .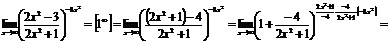

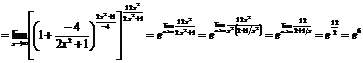Вопрос

Эквивалентные бесконечно малые

Вопрос

Непрерывность функции

Определение 1. Функция 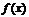называется непрерывной в точке 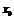, если она удовлетворяет следующим условиям:

1) определена в точке 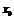, т.е. существует ;

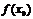2) имеет конечные односторонние пределы функции при 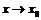слева и справа;

3) эти пределы равны значению функции в точке 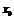, т.е.

.

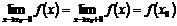Пример.Исследовать функции на непрерывность в точке :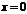

а) 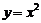, б) .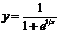

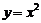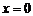Решение. а) . При функция определена, 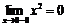, , 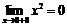, 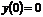т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция 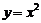в точке 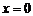непрерывна.

б) 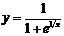. При 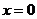функция не определена; ; .

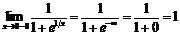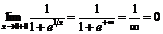Т.о. в точке 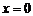функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.

Определение 2. Функция 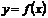называется непрерывной в точке 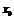, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: .

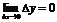Определения 1 и 2 равносильны.

Точка 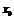называется точкой разрыва функции 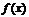, если эта функция в данной точке не является непрерывной. Различают точки разрыва:

Первого рода – когда существуют конечные односторонние пределы функции слева и справа при 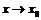, не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при 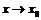существует, но не равен значению функции в этой точке.

Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.