Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу

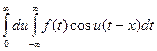
Тогда 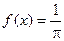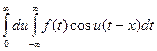- двойной интеграл Фурье.

Окончательно получаем:

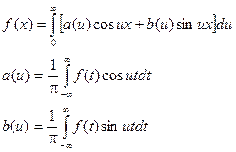
- представление функции f(x) интегралом Фурье.

Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:

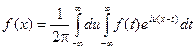
Преобразование Фурье.

Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция

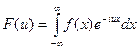
называется преобразованием Фурье функции f(x).

Функция F(u) называется также спектральной характеристикой функции f(x).

Если f(x) – функция, представимая интегралом Фурье, то можно записать:

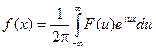
Это равенство называется обратным преобразованием Фурье

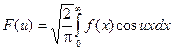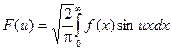Интегралы и называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.

Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.

Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.

Элементы теории функций комплексного переменного.

Определение. Если каждому комплексному числу z из некоторого множества D по некоторому закону поставлено в соответствие определенное комплексное число w из множества G, то на этой области задана однозначная функция комплексного переменного, отображающая множество D на множество G.

w = f(z)

Множество D называется областью определения, множество G – областью значений функции.

Комплексную функцию можно записать в виде:

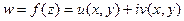
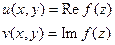
u, v – действительные функции от переменных х и у.

Если каждому zÎ D соответствует несколько различных значений w, то функция w=f(z) называется многозначной.

Определение. Функция 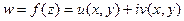имеет предел в точке z₀, равный числу А = a + ib, если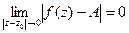

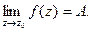
Свойства функций комплексного переменного.

Для функций комплексного переменного f(z) и g(z) справедливы следующие свойства:

1)

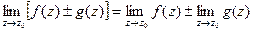
2)

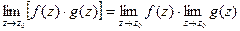
3)

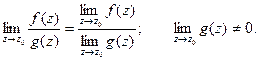
Определение. Функция 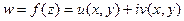называется непрерывной в точке z₀, если выполняется равенство

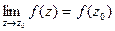
Основные трансцендентные функции.

Определение. Трансцендентными называются аналитические функции, которые не являются алгебраическими.

Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.

Рассмотрим разложение в степенной ряд следующих функций:

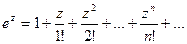
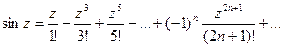
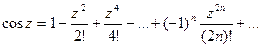
См. Представление функций по формуле Тейлора.

Функции e^z, cosz, sinz связаны между собой формулой Эйлера (см. Уравнение Эйлера.) Эта формула может быть очень легко получена сложением соотвествующих рядов.

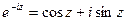
Также справедливы равенства:

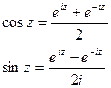
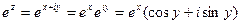
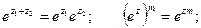
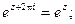
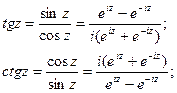
Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.

Определение. Гиперболическим синусом, косинусом, тангенсом и котангенсомназываются соответственно функции:

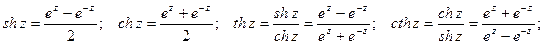
Гиперболические функции могут быть выражены через тригонометрические:

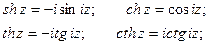
Гиперболические функции sh z и ch z имеют период 2pi, а функции th z и cth z – период pi.

Пример. Найти sin(1+2i).

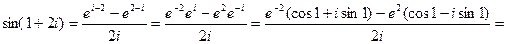
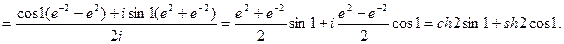
Определение. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.

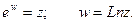
Если w = u + iv, то 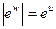и Arg e^w = 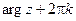= v.

Тогда e^u = .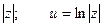

Итого: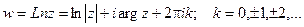

Для комплексного числа z = a + ib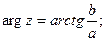

Определение. Выражение 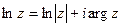называется главным значением логарифма.

Логарифмическая функция комплексного аргумента обладает следующими свойствами:

1)

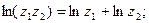
2)

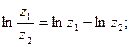
3)

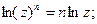
4)

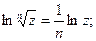
Обратные тригонометрические функции комплексного переменного имеют вид:

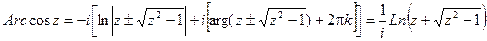
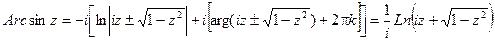
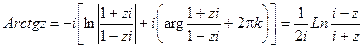
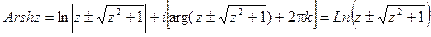
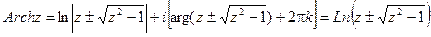
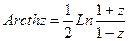
Производная функций комплексного переменного.

Определение. Производной от однозначной функции w = f(z) в точке z называется предел:

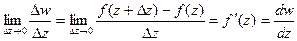
Определение. Функция f(z), имеющая непрерывную производную в любой точке области D называется аналитической функцией на этой области.

Правила дифференцирования функций комплексного аргумента не отличаются от правил дифференцирования функций действительной переменной.

Аналогично определяются производные основных функций таких как синус, косинус, тангенс и котангенс, степенная функция и т.д.

Производные гиперболических функций определяются по формулам:

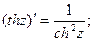
Вывод правил интегрирования, значений производных основных функций ничем не отличается от аналогичных операций с функциями действительного аргумента, поэтому подробно рассматривать их не будем.

Условия Коши – Римана.

(Бернхард Риман (1826 – 1866) – немецкий математик)

Рассмотрим функцию комплексной переменной 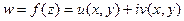, определенную на некоторой области и имеющую в какой – либо точке этой области производную

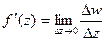
Стремление к нулю Dz®0 может осуществляться в следующих случаях:

1)

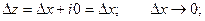
2)

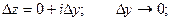
В первом случае:

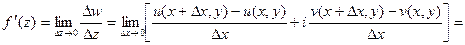
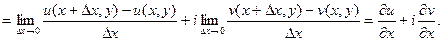
Во втором случае:

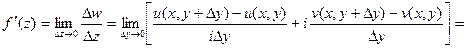
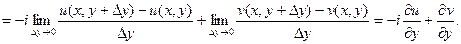
Тогда должны выполняться равенства:

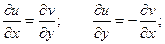
Эти равенства называются условиями Коши – Римана, хотя еще раньше они были получены Эйлером и Даламбером.

Теорема. Если функция 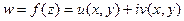имеет производную в точке

z = x + iy, то ее действительные компоненты u и v имеют в точке (х, у) частные производные первого порядка, удовлетворяющие условию Коши – Римана.

Также справедлива и обратная теорема.

На основании этих теорем можно сделать вывод, что из существования производной следует непрерывность функции.

Теорема. Для того, чтобы функция 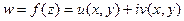была аналитической на некоторой области необходимо и достаточно, чтобы частные производные первого прядка функций u и v были непрерывны на этой области и выполнялись условия Коши – Римана.

Интегрирование функций комплексной переменной.

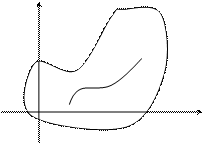
Пусть 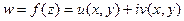- непрерывная функция комплексного переменного z, определенная в некоторой области и L – кривая, лежащая в этой области.

у

В

L

А

х

Кривая L задана уравнением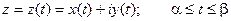

Определение. Интегралот функции f(z) вдоль кривой L определяется следующим образом:

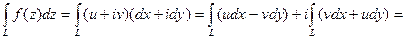
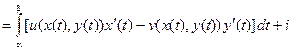
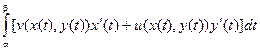
Если учесть, что , то

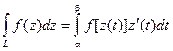
Теорема. (Теорема Коши) Если f(z) - аналитическая функция на некоторой области, то интеграл от f(z) по любому кусочно – гладкому контуру, принадлежащему этой области равен нулю.

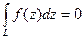
Интегральная формула Коши.

Если функция f(z) – аналитическая в односвязной замкнутой области с кусочно – гладкой границей L.

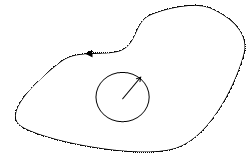
D

r

z₀

Тогда справедлива формула Коши:

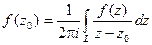
где z₀ – любая точка внутри контура L, интегрирование по контуру производится в положительном направлении (против часовой стрелки).

Эта формула также называется интегралом Коши.

Ряды Тейлора и Лорана.

(Пьер Альфонс Лоран (1813 – 1854) – французский математик)

Функция f(z), аналитическая в круге 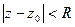, разлагается в сходящийся к ней степенной ряд по степеням (z – z₀).

Коэффициенты ряда вычисляются по формулам:

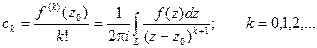
Степенной ряд с коэффициентами такого вида называется рядом Тейлора.

Рассмотрим теперь функцию f(z), аналитическую в кольце 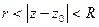. Эта функция может быть представлена в виде сходящегося ряда:

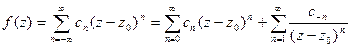
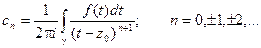
Ряд такого вида называется рядом Лорана. При этом функция f(z) может быть представлена в виде суммы:

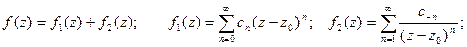
Ряд, определяющий функцию f₁(x), называется правильной частью ряда Лорана, а ряд, определяющий функцию f₂(x), называется главной частьюряда Лорана.

Если предположить, что r = 0, то можно считать, что функция аналитична в открытом круге 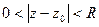за исключением центральной точки z₀. Как правило, в этой точке функция бывает не определена.

Тогда точка z₀ называется изолированной особой точкойфункции f.

Рассмотрим следующие частные случаи:

1) Функция f(x) имеет вид: 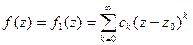. Т.к. степенной ряд сходится во всех точках внутри круга, то его сумма f₁(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре круга z₀.

В этом случае говорят, что особенность функции f в точке z₀ устранима. Для устранения особой точки достаточно доопределить функцию в центре круга (f(z₀) = c₀) и функция будет аналитической не только в окрестности центра круга, но и в самом центре.

В этом случае 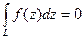для любого контура L, содержащего точку z₀ и принадлежащего к кругу .

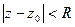2) Функция f(x) имеет вид: .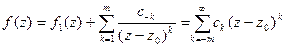

В этом случае точка z₀ называется полюсом функции f(z) порядка (кратности) m.При m = 1 точку z₀ называют еще простым полюсом.

Порядок полюса может быть определен по формуле:

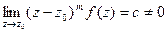
z₀ – полюс порядка т.

3) Функция f(z) имеет вид 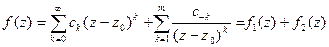, где в ряду 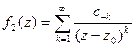не равно нулю бесконечное количество коэффициентов с_-k.

В этом случае говорят, что функция f(z) имеет в точке z₀ существенно особую точку.

Определение. Пусть z₀ – изолированная особая точка функция f(z), т.е. пусть функция f(z) – аналитическая в некотором круге 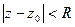из которого исключена точка z₀. Тогда интеграл

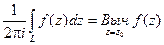
называется вычетом функции f(z) в точке z₀, где L – контур в круге 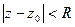, ориентированный против часовой стрелки и содержащей в себе точку z₀.

Вычет также обозначают иногда .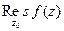

Если 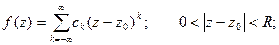есть ряд Лорана функции f в точке z₀, то .

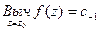Таким образом, если известно разложение функции в ряд Лорана, то вычет легко может быть найден в случае любой особой точки.

В частных случаях вычет может быть найден и без разложения в ряд Лорана.

Например, если функция 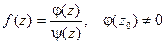, а 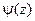имеет простой нуль при z = z₀ 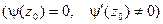, то z = z₀ является простым полюсом функции f(z).

Тогда можно показать, что вычет находится по формуле

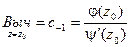
Если z = z₀ – полюс порядка m ³ 1, то вычет может быть найден по формуле:

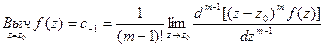
Пример. Найти вычет функции 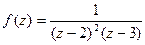относительно точки z = 2.

Эта точка является полюсом второго порядка. Получаем:

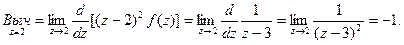
Теорема о вычетах.

Теорема. Пусть функция f(z) – аналитическая на всей плоскости z, за исключением конечного числа точек z₁, z₂, …, z_N. Тогда верно равенство:

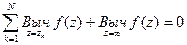
А интеграл от функции по контуру L, содержащему внутри себя эти точки, равен

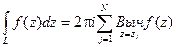
Эти свойства применяются для вычисления интегралов. Если функция f(z) аналитическая в верхней полуплоскости, включая действительную ось, за исключением N точек, то справедлива формула

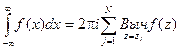
Пример. Вычислить определенный интеграл .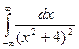

Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.

Найдем вычет функции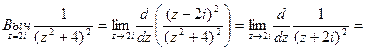

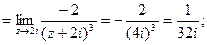
Получаем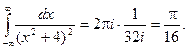

Пример. Вычислить определенный интеграл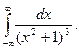

Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.

Найдем вычет функции

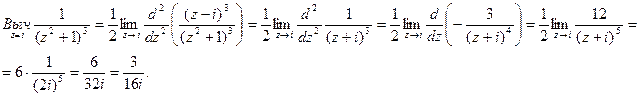
Получаем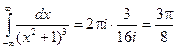

Операционное исчисление.

Преобразование Лапласа.

(Пьер Симон Лаплас (1749 – 1825) – французский математик)

Рассмотрим функцию действительного переменного t, определенную при t ³ 0. Будем также считать, что функция f(t)- кусочно - непрерывная, т.е. в любом конечном интервале она имеет конечное число точек разрыва первого рода, и определена на бесконечном интервале (-¥, ¥), но f(t) = 0 при t < 0.

Будем считать, что функция ограничена условием:

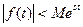
Рассмотрим функцию

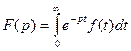
где p = a + ib – комплексное число.

Определение. Функция F(p) называется изображением Лапласафункции f(t).

Также функцию F(p) называют L – изображениемили преобразованием Лапласа.

Обозначается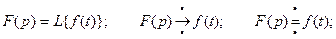

При этом функция f(t) называется начальной функциейили оригиналом, а процесс нахождения оригинала по известному изображению называется операционным исчислением.

Теорема. (Теорема единственности) Если две непрерывнные функции f(x) и g(x) имеют одно и то же L – изображение F(p), то они тождественно равны.

Определение. Функцией Хевисайда (Оливер Хевисайд (1850 – 1925) – английский физик) называется функция

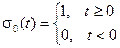
Свойства изображений.

Если 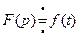, то справедливы следующие свойства:

1) Свойство подобия.

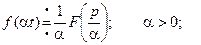
2) Свойство линейности.

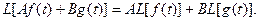
3) Смещение изображения.

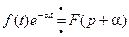
4) Дифференцирование изображения.

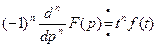
5) Дифференцирование оригинала.

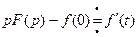
6) Интегрирование изображения.

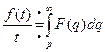
(Справедливо при условии, что интеграл сходится)

7) Интегрирование оригинала.

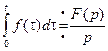
Таблица изображений некоторых функций.

Для большинства функций изображение находится непосредственным интегрированием.

Пример. Найти изображение функции f(t) = sint.

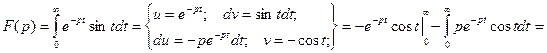
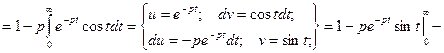
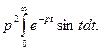
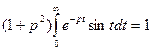
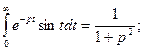
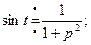
Для многих функций изображения посчитаны и приведены в соответствующих таблицах.

№	f(t)	F(p)	№	f(t)	F(p)
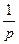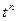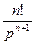	sinat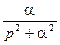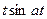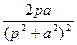
	cosat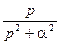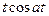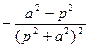
	e-at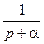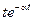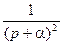
	shat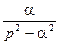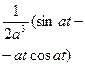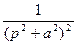
	chat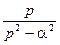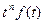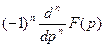
					*

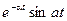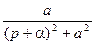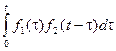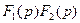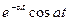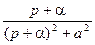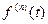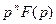* - при условии, что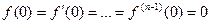

Теоремы свертки и запаздывания.

Теорема. (теорема запаздывания) Если f(t) = 0 при t < 0, то справедлива формула

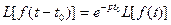
где t₀ – некоторая точка.

Определение. Выражение 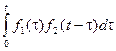называется сверткойфункций f₁(t) и f₂(t) и обозначается f₁* f₂.

Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций f₁(t) и f₂(t) .

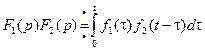
Теорема. (Интеграл Дюамеля (Дюамель (1797 – 1872) – французский математик)). Если 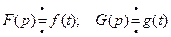, то верно равенство

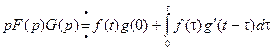
Для нахождения изображений различных функций наряду с непосредственным интегрированием применяются приведенные выще теоремы и свойства.

Пример. Найти изображение функции .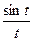

Из таблицы изображений получаем: .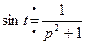

По свойству интегрирования изображения получаем: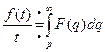

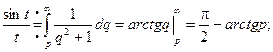
Пример. Найти изображение функции .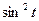

Из тригонометрии известна формула .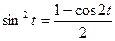

Тогда = .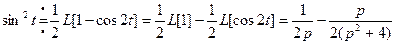

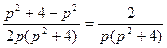Операционное исчисление используется как для нахождения значений интегралов, так и для решение дифференциальных уравнений.

Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.

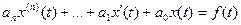
Требуется найти решение этого дифференциального уравнения, удовлетворяющее начальным условиям:

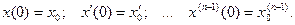
Если функция x(t) является решением этого дифференциального уравнения, то оно обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция f(t) имеет (по теореме единственности) одно и то же изображение Лапласа.

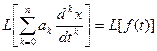
Из теоремы о дифференцировании оригинала { 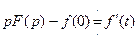} можно сделать вывод, что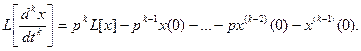

Тогда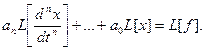

Обозначим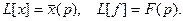

Получаем: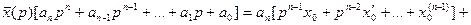

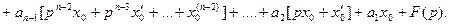
Это уравнение называется вспомогательным (изображающим)илиоператорным уравнением.

Отсюда получаем изображение 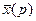, а по нему и искомую функцию x(t).

Изображение получаем в виде: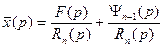

Где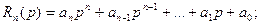

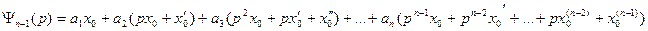Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:

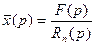
Рассмотрим применение этого метода на примерах.

Пример. Решить уравнение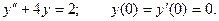

Изображение искомой функции будем искать в виде:

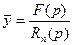
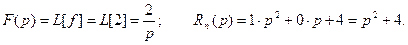
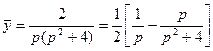
Находим оригинал, т.е. искомую функцию: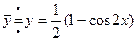

Пример. Решить уравнение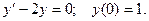

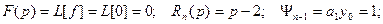
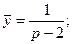
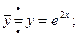
Пример. Решить уравнение:

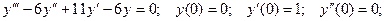
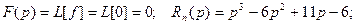
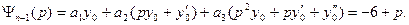
Изображение искомой функции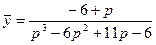

Для нахождения оригинала необходимо разложить полученную дробь на элементарные дроби. Воспользуемся делением многочленов (знаменатель делится без остатка на p – 1):

p³ – 6p² + 11p – 6 p - 1

p³ – p² p² – 5p + 6

-5p² + 11p

-5p² + 5p

6p - 6

6p - 6

В свою очередь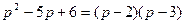

Получаем: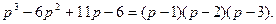

Тогда: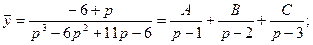

Определим коэффициенты А, В и С.

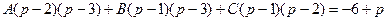
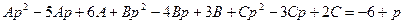
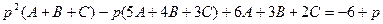
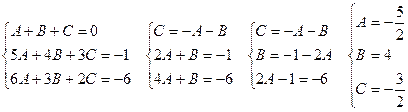
Тогда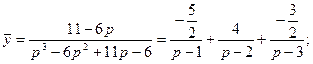

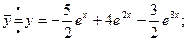
Приемы операционного исчисления можно также использовать для решения систем дифференциальных уравнений.

Пример. Решить систему уравнений:

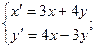
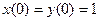
Обозначим 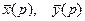- изображения искомых функций и решим вспомогательные уравнения:

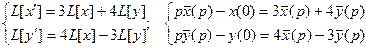
Решим полученную систему алгебраических уравнений.

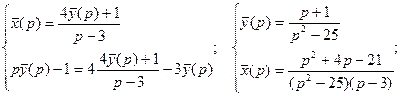
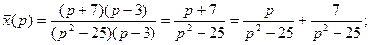
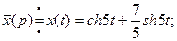
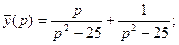
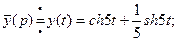
Если применить к полученным результатам формулы

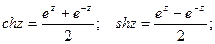
то ответ можно представить в виде:

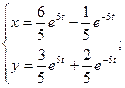
Как видно, гиперболические функции в ответе могут быть легко заменены на показательные.

Пример. Решить систему уравнений

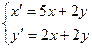при x(0) = y(0) = 1

Составим систему вспомогательных уравнений:

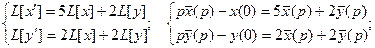
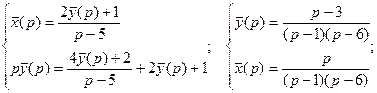
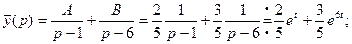
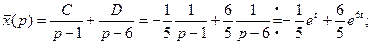
Если обозначить 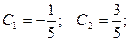то из полученного частного решения системы можно записать и общее решение:

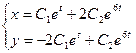
При рассмотрении нормальных систем дифференциальных уравнений этот пример был решен традиционным способом (См. Другой способ решения.). Как видно, результаты совпадают.

Отметим, что операторный способ решения систем дифференциальных уравнений применим к системам порядка выше первого, что очень важно, т.к. в этом случае применение других способов крайне затруднительно.

Криволинейные интегралы.

Определение. Кривая 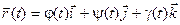( 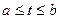) называется непрерывной кусочно – гладкой, если функции j, y и g непрерывны на отрезке [a,b] и отрезок [a,b] можно разбить на конечное число частичных отрезков так, что на каждом из них функции j, y и g имеют непрерывные производные, не равные нулю одновременно.

Если определено не только разбиение кривой на частичные отрезки точками, но порядок этих точек, то кривая называется ориентированннойкривой.

Ориетированная кривая называется замкнутой, если значения уравнения кривой в начальной и конечной точках совпадают.

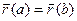
Рассмотрим в пространсве XYZ кривую АВ, в каждой точке которой определена произвольная функция .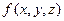

Разобьем кривую на конечное число отрезков и рассмотрим произведение значения функции в каждой точке разбиения на длину соответствующего отрезка.

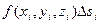
Сложив все полученные таким образом произведения, получим так называемую интегральнуюсумму функции f(x, y, z).

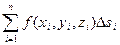
Определение. Если при стремлении к нулю шага разбиения кривой на частичные отрезки существует предел интегральных сумм, то этот предел называется криволинейным интегралом от функции f(x, y, z) по длине дуги АВили криволинейным интегралом первого рода.

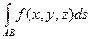
Свойства криволинейного интеграла первого рода.

1) Значение криволинейного интеграла по длине дуги не зависит от направления кривой АВ.

2) Постоянный множитель можно выносить за знак криволинейного интеграла.

3) Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций.

4) Если кривая АВ разбита на дуга АС и СВ, то

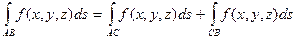
5) Если в точках кривой АВ

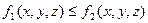
то

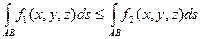
6) Справедливо неравенство:

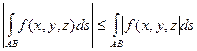
7) Если f(x, y, z) = 1, то

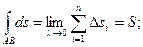
S – длина дуги кривой, l - наибольшая из всех частичных дуг, на которые разбивается дуга АВ.

8) Теорема о среднем.

Если функция f(x, y, z) непрерывна на кривой АВ, то на этой кривой существует точка (x₁, y₁, z₁) такая, что

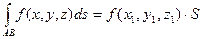
Для вычисления криволинейного интеграла по длине дуги надо определить его связь с обыкновенным определенным интегралом.

Пусть кривая АВ задана параметрически уравнениями x = x(t), y = y(t), z = z(t),

a £ t £ b, где функции х, у, z – непрерывно дифференцируемые функции параметра t, причем точке А соответствует t = a, а точке В соответствует t = b. Функция f(x, y, z) – непрерывна на всей кривой АВ.

Для любой точки М(х, у, z) кривой длина дуги АМ вычисляется по формуле

(См. Вычисление длины дуги кривой.):

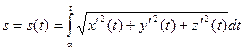
Длина всей кривой АВ равна:

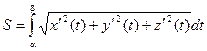
Криволинейный интеграл по длине дуги АВ будет находиться по формуле:

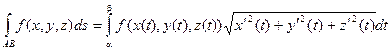
Таким образом, для вычисления криволинейного интеграла первого рода (по длине дуги АВ) надо, используя параметрическое уравнение кривой выразить подынтегральную функцию через параметр t, заменить ds дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.

Пример. Вычислить интеграл 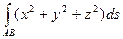по одному витку винтовой линии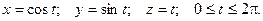

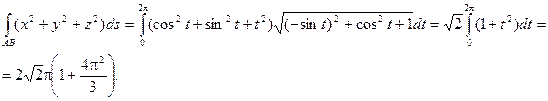
Если интегрирование производится по длине плоской кривой, заданной уравнением 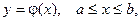то получаем:

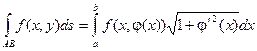
Криволинейные интегралы второго рода.

Пусть АВ – не