Вопрос 2.Кольцо матриц над полем действительных чисел. Основные операции над матрицами. Свойства операций.

Матрицей называется прямоугольная таблица чисел.

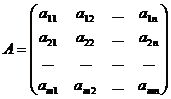
А – матрица, 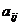- элемент матрицы, 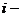номер строки, в которой стоит данный элемент, 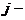номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Определение.Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида:

= E,

называетсяединичной матрицей.

Операции над матрицами:

Сложение (вычитание) матриц – складывать (вычитать) по элементам и только над матрицами одинаковой размерности.

Например:

Сложить матрицы 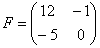и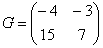

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

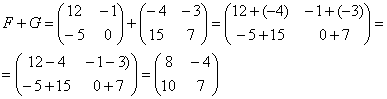
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

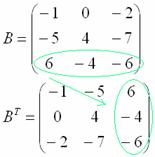
2) Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример:

Транспонировать матрицу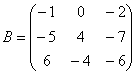

Умножение матрицы на число , произведение.

Пример:

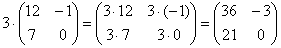
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Умножение матриц.

mxnи nxq, называется матрица размерности mxq.

Количество столбцов 1-ой матрицы должно совпадать с количеством строк 2-ой матрицы.

Умножение происходит таким образом, берется 1 строка 1-ой матрицы и умножается на 1 столбец 2-ой матрицы, далее 1 строка 1-ой матрицы умножается на 2 столбец 2-ой матрицы и т.д и получится 1 строка НОВОЙ МАТРИЦЫ.

Пример:

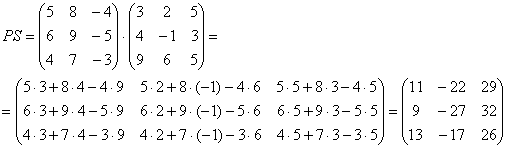
Свойства умножения матриц:

· 1.ассоциативность (AB)C = A(BC);

· 2.некоммутативность (в общем случае): AB 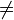BA;

· 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

· 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB)

Коммуникативность:

Умножение матриц не коммуникативно, и даже в том случае, когда матрицы квадратные все равно 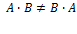, например имеется 2 матрицы 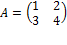и 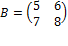результатом умножения матрицы А на матрицу Bбудет матрица 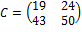, а если мы матрицу Bумножим на матрицу А получится 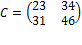. Множество квадратный матриц mxn замкнуто относительно умножения

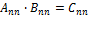. Множество матриц nxm обладают мультипликативной единицей ,

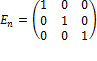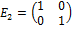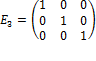, . Действительно, если перемножить матрицу 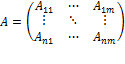и 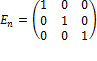, то получим =>

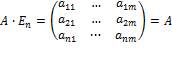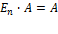
Ассоциативность:

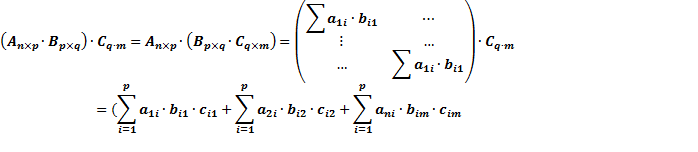
Вопрос 3. Определители. Теорема Лапласа. Свойства определителей.

Определитель– это число, которое считается по определенному правилу.

Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов.

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

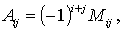
1)Определитель можно посчитать только у квадратной матрицы.

2) Определитель матрицы |An|=An

3)Определитель матрицы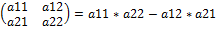

5) Для вычисления матрицы 3x3 существует правило треугольников (Правило Саррюса)

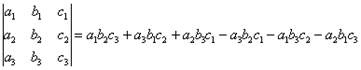
Если дана матрица 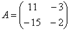, то ее определитель обозначают 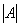. Также очень часто определитель обозначают латинской буквой 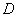или греческой .