Второй замечательный предел: Главное, что Х стремится к бесконечности.

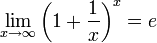или

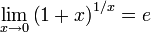
Следствия:

1.

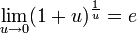
2.

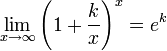
3.

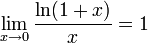
4.

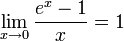
5. 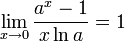для ,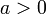

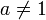
6.

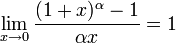
35. Сравнение бесконечно малых, эквивалентные б.м.

Определение 1. Функци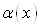и и 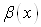называются бесконечно малыми величинами одного порядка малости, если .

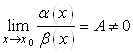Определение 2. Функция 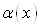называется бесконечно малой величиной более высокого порядка малости, чем 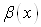, если .

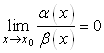Определение 3. Функция 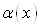называется бесконечно малой величиной более низкого порядка малости, чем 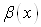, если .

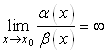Тот факт, что 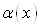, например, имеет более высокий порядок малости, чем 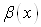, можно обозначить следующим образом: .

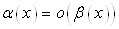Определение 4.Функци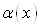и и 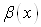называются несравнимыми бесконечно малыми величинами, если 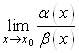не существует и не равен .

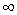Если 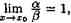то α и ß называются эквивалентными бесконечно малыми (при х→x₀); это обозначается так: α~ß.

Теорема 1. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Теорема 2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.

Теорема 3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.

36. Непрерывность функции в точке.

Определение 1.Функция f(x) называется непрерывной в точке х_0, если она удовлетворяет следующим трем условиям:

1)определена в точке х₀ (т.е.существует f(х₀))

2)имеет конечный предел функции при х→х_о

3)этот предел равен значению функции в точке х₀, т.е.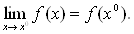

Определение 2.Функция y=f(x) называется непрерывной в точке х₀ если онаопределена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

lim (где дельта Х стремится к нулю) Дельта У = 0

(надеюсь поймешь тут мою надпись, не могу в инете найти чтоб четко было(( )

37. Точки разрыва, их классификация.

Точка х₀ называется точкой разрыва функции f (x), если f (x) в точке х₀ не является непрерывной.
Это значит, что или не существует предела функции в данной точке, или этот предел не совпадает с тем значением, которое функция принимает в этой точке.

Классификация:
1)Точка х₀ называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы

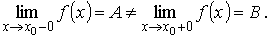
2)Точка х₀ называется точкой разрыва второго рода функции f(x), если в этой точке функция f (x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Так для функции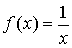

в точке х = 0 односторонние пределы равны

,

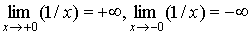то х = 0 является точкой разрыва второго рода.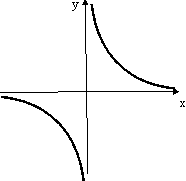

38. Операции над непрерывными функциями, свойства непрерывных функций

Свойства непрерывных функций в точке:

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций 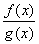– есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.

Свойства непрерывных функции на отрезке:

1)Если функции y=f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке.

2) Если функция y=f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения M (теорема Вейерштрасса).

3) Если функция y=f(x) непрерывна на отрезке [a, b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка E принадлежавшая (a,b), такая, что f(E)=0 (теорема Больцано-Коши).