Расчет статически неопределимых систем методом сил.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методическое пособие для студентов заочной формы обучения (сокращенный срок подготовки) специальностей 190201, 190601, 151001, 151002, 150201, 150202, 270102, 270112
Тольятти 2007
1. Маршрутизатор по дисциплине «Сопротивление материалов»
Курс «Сопротивление материалов» для студентов заочной формы обучения сокращенного срока подготовки базируется на знаниях, полученных в колледжах. Обычно это знания о расчете на прочность и жесткость статически определимых элементов конструкций, испытывающих простые виды деформаций (растяжение-сжатие, кручение, плоский прямой изгиб), о расчете на устойчивость стержней прямолинейной формы и на выносливость в условиях одноосного напряженного состояния. Инженерные знания должны быть дополнены важными разделами такими как:
1. Расчет на прочность элементов конструкций в условиях сложного сопротивления.
2. Методы расчета статически неопределимых систем.
3. Расчет на прочность и жесткость в условиях динамического воздействия нагрузки.
Распределение часов по дисциплине «Сопротивление материалов»
для студентов инженерных специальностей заочной формы обучения
(сокращенный срок подготовки)
| Название специальность | 7 семестр | 8 семестр | ||||||||
| Лекц. (час.) | Лаб. (час.) | Прак. (час.) | Конт. Раб. | Итог контр. | Лекц. | Лаб. | Прак. | Конт. раб. | Итог контр. | |
| МиТОМД, АиТ, АиАХ, ОТСП, ПГС, ВиВ, ТМ, МСиК | - | - | - | Э |
МиТОМД- Машины и технология обработки металлов давлением
АиТ - Автомобиле и тракторостроение
АиАХ - Автомобили и автомобильное хозяйство
ОТСП - Оборудование и технология сварочного производства
ПГС - Промышленно гражданское строительство
ВиВ - Водоснабжение и водоотведение
ТМ - Технология машиностроения
МСиК - Металлообрабатывающие станки и комплексы
| Тип занятия | Темы занятий | Количество часов |
| Лекция |
| |
| Практическое занятие |
| |
| Лабораторное занятие |
|
Для закрепления знаний по перечисленным темам предусматривается выполнение контрольной работы, в которую включены три задачи:
- Расчет на прочность при сложном сопротивлении.
Расчет статически неопределимых систем методом сил.
- Расчет на прочность и жесткость балки при поперечном ударе.
Краткая программа теоретического курса
2.1. Расчет на прочность элементов конструкций в общем случае нагружения.
| Базовые знания · Построение эпюр ВСФ на пространственных стержневых конструкциях · Расчет на прочность и жесткость при растяжении-сжатии, изгибе, кручении |
Основы теории напряженно-деформированного состояния в точке
Задача.
В стержне с площадью поперечного сечения A=5х104 м2, растягиваемом силой F = 50 кН, определить нормальное и касательное напряжения, возникающие на площадке, наклоненной под углом 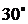 к поперечному сечению стержня:
к поперечному сечению стержня:
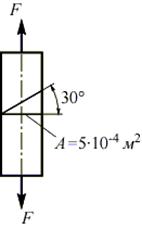
В точках поперечного сечения возникают только нормальные напряжения, то есть площадка элементарного объема в окрестностях точки, совпадающая с этим сечением, является главной:
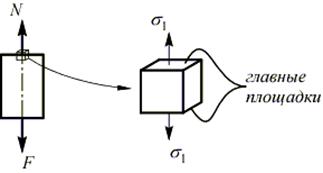
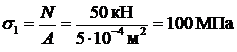 ,
,
остальные главные напряжения отсутствуют, т.е. это одноосное напряженное состояние.
Найдем напряжения на наклонной площадке.
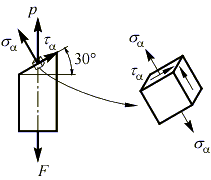
Вектор полного напряжения p, действующий на этой площадке, можно разложить на две составляющие: нормальную sa и касательную ta, для определения величины которых воспользуемся кругом Мора.
Наносим в координатах t-s точки, соответствующие главным напряжениям 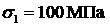 и
и 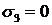 , и на этих точках, как на диаметре, строим круг Мора:
, и на этих точках, как на диаметре, строим круг Мора:
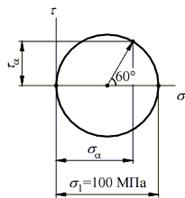
Откладывая от оси абсцисс против часовой стрелки двойной угол a, получаем на круге точку, отображающую состояние на наклонной площадке. Координаты этой точки являются искомыми напряжениями и вычисляются по формулам (2.4) и (2.5):
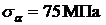 ,
, 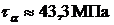 .
.
Обратная задача Мора
Обратная задача Мора состоит в определении главных напряжений по известным напряжениям на произвольной площадке. Рассмотрим её на конкретном примере.
Задача.
Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения:
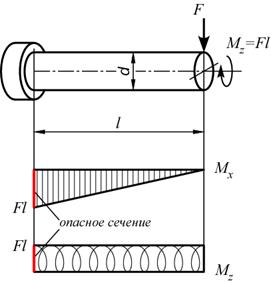
Построив эпюры внутренних силовых факторов, заключаем, что опасным сечением стержня является сечение заделки, в котором действует наибольший по величине изгибающий момент Mx.
Для нахождения опасной точки в опасном сечении рассмотрим распределение нормальных и касательных напряжений по опасному сечению:
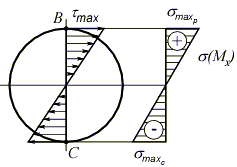
В данном случае имеется две равноопасные точки – B и C, в которых действуют максимальные нормальные и касательные напряжения, одинаковые по величине, но разные по направлению. Рассмотрим напряженное состояние в точке В, выделив в её окрестности элементарный объем и расставив вектора напряжений 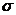 и
и 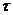 на его гранях.
на его гранях.
Величины напряжений 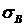 и
и 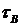 можно определить по формулам:
можно определить по формулам:
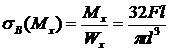 ,
,
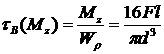 .
.
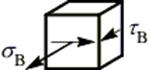
Рассмотрим выделенный куб со стороны грани, свободной от напряжений (сверху):
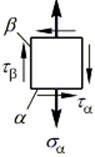
Обозначим две взаимно перпендикулярные площадки a и b. На площадке a действуют нормальное 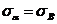 и касательное напряжение
и касательное напряжение 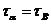 . На площадке b действуют только касательное напряжение
. На площадке b действуют только касательное напряжение 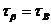 (согласно закону парности касательных напряжений).
(согласно закону парности касательных напряжений).
Порядок построения круга Мора:
1. В системе координат t-s нанести точки с координатами 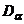 (sa, ta) и
(sa, ta) и 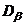 (sb, tb). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
(sb, tb). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
2. Соединить полученные точки Da и Db отрезком. Точка пересечения этого отрезка с осью абсцисс O является центром круга Мора.
3. Построить окружность с центром в точке O и радиусом ODa. Координаты точек пересечения окружности с осью абсцисс дают величины главных напряжений (в нашем случае s1, и s3).
4. Пересечение площадок a (горизонталь) и b (вертикаль) дает положение полюса площадок круга Мора Pпл (точка, в которой пересекаются все площадки).
5. Провести из полюса Pпл лучи через точки (s1, 0) и (s3, 0). Эти лучи задают положение главных площадок.
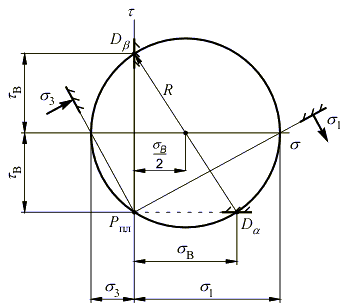
Наносим положение главных площадок и направление главных напряжений на рассматриваемую площадку:
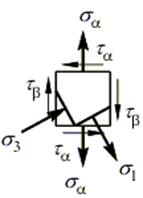
Радиус круга Мора
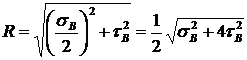 ,
,
тогда главные напряжения
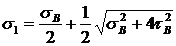 ,
,
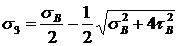 .
.
Теории хрупкого разрушения
Первая теория прочности – теория наибольших нормальных напряжений (теория Галилея).
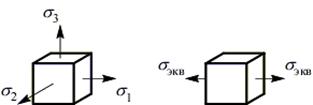
Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие нормальные напряжения
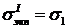 .
.
Условие прочности при растяжении
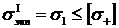 .
.
Также можно использовать условие прочности для сжатия
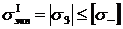 . (2.7)
. (2.7)
Данная теория нашла подтверждение только для весьма хрупких материалов (камень, бетон, кирпич). Ее основным недостатком является неучет двух главных напряжений.
Вторая теория прочности – теория наибольших линейных деформаций (теория Мариотта).
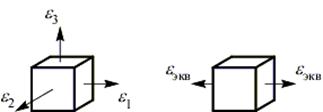
Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие линейные относительные деформации
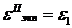 .
.
Согласно закону Гука, при одноосном напряженном состоянии
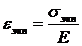 .
.
Наибольшую линейную относительную деформацию при произвольном напряженном состоянии запишем, используя обобщенный закон Гука:
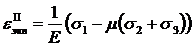 .
.
Приравнивая правые части, получим эквивалентное напряжение по второй теории
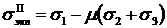 . (2.8)
. (2.8)
Вторая теория применима только для хрупких материалов, в том числе для хрупких металлов.
Теории пластичности
Третья теория прочности – теория наибольших касательных напряжений (теория Кулона).
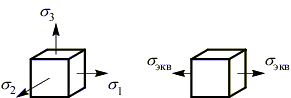
Критерий равнопрочности: напряженных состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны наибольшие касательные напряжения
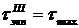 .
.
По формуле (2.2) касательное напряжение в случае плоского напряженного состояния определяется как:
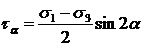 ,
,
из которой следует, что
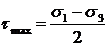 .
.
При одноосном напряженном состоянии 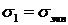 ,
, 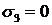 , и
, и
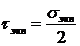 .
.
Приравнивая правые части полученных выражений, получим эквивалентное напряжение по третьей теории
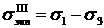 .
.
Для случая плоского напряженного состояния, когда нормальное напряжение на одной из площадок равно нулю (изгиб с кручением), выразив главные напряжения через напряжения на произвольной площадке, условие прочности принимает вид:
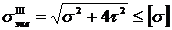 . (2.9)
. (2.9)
Третья теория используется при расчете элементов конструкций, изготовленных из пластичных материалов. Ее недостатком является неучет главного напряжения σ2.
Четвертая теория прочности – теория удельной потенциальной энергии формоизменения – энергетическая теория (теория Мизеса – Генки).
Критерий равнопрочности: напряженные состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны удельные потенциальные энергии формоизменения:
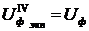 .
.
Используя приведенное в разделе 8.1.5 выражение для потенциальной энергии изменения формы (8.1) для одноосного и объемного напряженного состояния, получим
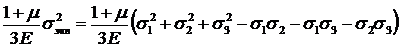 ,
,
откуда эквивалентное напряжение по четвертой теории
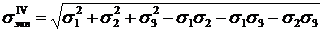 .
.
Для случая плоского напряженного состояния ( 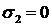 ):
):
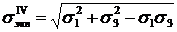 . (2.10)
. (2.10)
Выражая главные напряжения через напряжения на произвольных площадках для плоского напряженного состояния, когда на одной из площадок нормальное напряжение равно нулю, получим:
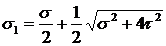 и
и 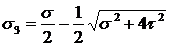 .
.
Подставляя полученные выражения в формулу (8.6), условие прочности можно записать в виде:
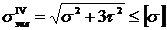 .
.
Энергетическая теория хорошо согласуется с экспериментальными данными (лучше, чем третья теория), и широко используется для пластичных материалов.
Универсальная теория Мора
Пятая теория прочности – теория предельных состояний (теория Мора).
Критерий равнопрочности: напряженные состояния равнопрочны по наступлению предельного состояния, если при одновременном пропорциональном увеличении главных напряжений их круги Мора одновременно коснутся предельной огибающей.
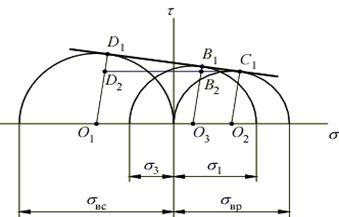
Если изобразить в координатах t-s семейство кругов Мора для различных предельных состояний материала, то огибающая этого семейства будет предельной огибающей для данного материала.
Изобразим в координатах t-s три предельных круга Мора:
- круг с центром в точке O1 – для случая одноосного сжатия (главные напряжения σ1 = 0, σ2 = 0, σ3 = σвс);
- круг с центром в точке O2 – для случая одноосного растяжения (главные напряжения σ1 = σвр, σ2 = 0, σ3 = 0);
- круг с центром в точке O3 – для случая плоского напряженного состояния (главные напряжения σ1, σ3).
Линия C1D1, огибающая круги, называется предельной огибающей.
Как видно из рисунка, 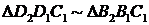 , то есть
, то есть
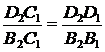 .
.
Запишем длины отрезков через соответствующие напряжения:
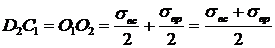 ,
,
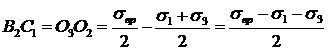 ,
,
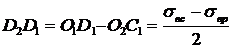 ,
,
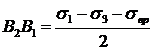 .
.
Подставляя эти значения в пропорцию, получим
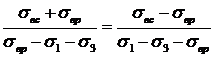 ,
,
откуда:
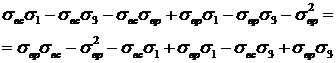 .
.
После сокращения имеем
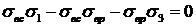 ,
,
тогда
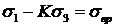 , где
, где 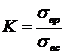 .
.
Т.к. 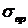 – предел прочности для одноосного растяжения, его можно заменить
– предел прочности для одноосного растяжения, его можно заменить 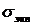 .
.
Таким образом, эквивалентное напряжение по теории Мора, равно:
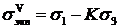 . (2.11)
. (2.11)
Для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию, 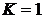 , следовательно
, следовательно
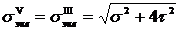 ,
,
то есть теория Мора совпадает с теорией максимальных касательных напряжений.
Для хрупких материалов 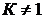 , и
, и
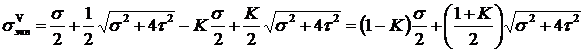 .
.
Интересно, что для весьма хрупких материалов с 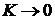
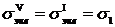 ,
,
то есть теория Мора совпадает с теорией максимальных нормальных напряжений.
Теорию Мора рекомендуется использовать для хрупких (в том числе анизотропных) материалов вместо первой и второй теорий. Ее недостатком является неучет промежуточного главного напряжения σ2.
Общий случай нагружения
Сочетание изгиба в двух плоскостях с растяжением (сжатием) и кручением называется общим случаем нагружения.
Рассмотрим алгоритм расчета на прочность в общем случае нагружения на примере консольной балки прямоугольного поперечного сечения, изготовленной из пластичного материала:
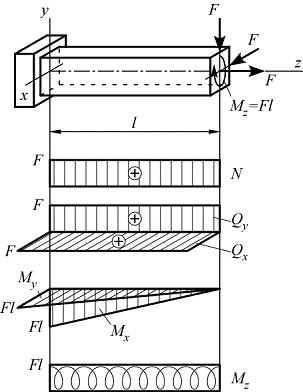
На рисунке показаны эпюры распределения внутренних силовых факторов вдоль оси балки.
Требования к знаниям и умениям по данному разделу
Что надо знать: Что такое напряженное состояние в точке нагруженного элемента конструкции. Понятие о главных напряжениях. Виды напряженного состояния в точке. Что такое прямая и обратная задачи О.-К. Мора, и как они решаются. Что такое деформированное состояние в точке. Понятие о главных деформациях. Математическую формулировку закона Гука для объемного деформированного состояния. Что такое теории предельного состояния и их назначение. Понятие об эквивалентном напряжении σэкв. Математические выражения σэкв для пяти классических теорий предельного состояния.
Что надо уметь: По условиям нагружения элемента конструкции определять положение опасного сечения и вид деформации в опасном сечении. Определять положение опасной точки в опасном сечении. Вид напряженного состояния в опасной точке. Соответственно виду напряженного состояния и в зависимости от механических свойств материала выбирать теорию предельного состояния для расчета эквивалентного напряжения.
Алгоритм
расчета на прочность в условиях сложного сопротивления
- Определение положения опасного сечения на элементе конструкции. Рекомендации: Для реализации этого пункта постройте эпюры внутренних силовых факторов.
- Определение вида деформации в опасном сечении.
Рекомендации: Необходимо учитывать сочетание внутренних силовых факторов и формы поперечного сечения. - Определение положения опасной точки в опасном сечении.
Рекомендации: При изгибе необходимо определить положение нейтральной линии, т.к. опасные точки находятся на максимальном удалении от нейтральной линии. - Определение вида напряженного состояния в опасной точке.
- Выбор теории предельного состояния для определения эквивалентного напряжения в опасной точке и решение условия прочности.
Рекомендации: При выборе теории предельного состояния руководствоваться свойствами используемого материала (хрупкий или пластичный).
Метод сил
Основная идея метода сил заключается в том, чтобы заменить исходную статически неопределимую систему эквивалентной статически определимой. Для этого в заданной статически неопределимой системе отбрасывают «лишние» связи (так, чтобы она стала статически определимой, но при этом оставалась кинематически неизменяемой) и заменяют их реакциями. Реакции отброшенных связей (так называемые «лишние» неизвестные) определяют из условия эквивалентности двух систем: заданной статически неопределимой и полученной статически определимой. Условием эквивалентности является требование равенства нулю перемещений раскрепленных точек системы в направлении отброшенных связей.
Проследим применение алгоритма метода сил на примере трех конструкций, рассмотренных в Таблице 1, испытывающих различные виды деформации. Результаты отражены в Таблице 2.
Алгоритм метода сил
Образование основной системы.
Основная система образуется из исходной путем отбрасывания лишних связей и факторов внешнего воздействия. Основная система должна быть статически определима и кинематически неизменяема. Выбор основной системы неоднозначен.
В строке №2 Таблицы 2 показаны возможные варианты выбора основной системы для рассматриваемых расчетных схем.
Образование эквивалентной системы.
Эквивалентная система образуется из основной путем замены отброшенных связей их неизвестными реакциями и приложением факторов внешнего воздействия. Реакции отброшенных связей в методе сил принимают за неизвестные и обозначают: Х1, Х2,…,Хn (для n раз статически неопределимой системы: s=n).
Остановимся для наших примеров на вариантах №1 выбора основной системы, тогда в строке №3 Таблицы 2 показаны соответствующие им эквивалентные системы.
Построение эпюр ВСФ.
Эпюры внутренних силовых факторов исходной статически неопределимой системы строятся по эквивалентной статически определимой системе с учетом заданной внешней нагрузки и найденных значений «лишних» неизвестных. Эти эпюры будем называть суммарными и обозначать индексом « 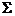 » (см. строку №11 Таблицы 2).
» (см. строку №11 Таблицы 2).
Задача.
Дана абсолютно жесткая балка ВС, закрепленная с помощью шарнирно-неподвижной опоры «О» и 2-х податливых стержней, и нагруженная двумя силами 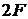 и
и 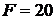 кН (рис. 1.1). В процессе эксплуатации оба стержня нагреваются на
кН (рис. 1.1). В процессе эксплуатации оба стержня нагреваются на 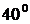 С. Стержень №2 изготовлен короче необходимого размера на
С. Стержень №2 изготовлен короче необходимого размера на 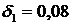 % l. Площадь поперечного сечения стержней
% l. Площадь поперечного сечения стержней 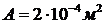 ,
, 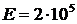 МПа; коэффициент линейного расширения материала стержней
МПа; коэффициент линейного расширения материала стержней 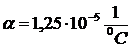 ,
, 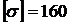 МПа.
МПа.
Определить напряжения, возникающие в стержнях от каждого из действующих факторов, а также суммарные напряжения. Сделать вывод о работоспособности системы в целом.
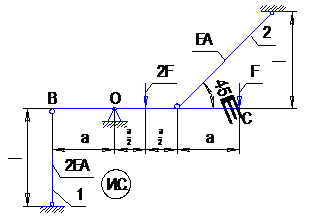 |
| Рис. 3.1. Исходная система |
Решение:
1. Образуем основную систему (рис. 3.2):
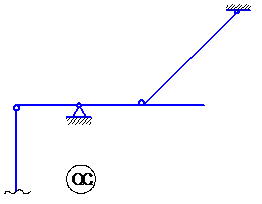 |
| Рис. 3.2. Основная система |
2. Образуем эквивалентные системы (рис. 3.3 а, рис. 3.3 б, рис. 3.3 в):
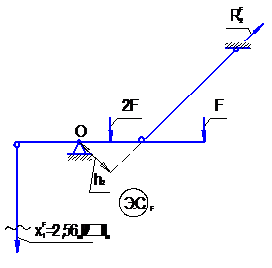 |
| Рис. 3.3, а. Эквивалентная система с воздействием силового фактора |
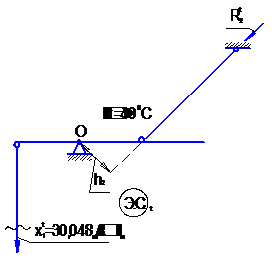 |
| Рис. 3.3, б. Эквивалентная система с воздействием температуры |
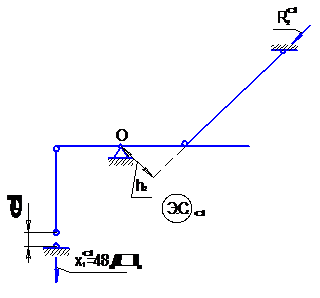 |
| Рис. 3.3, в. Эквивалентная система с неточностью изготовления |
3. Для каждой эквивалентной системы запишем условие эквивалентности:
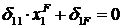 – для (эквивалентной системы – F). – для (эквивалентной системы – F). | (3.2) |
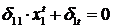 – для (эквивалентной системы – t). – для (эквивалентной системы – t). | (3.3) |
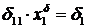 – для (эквивалентной системы – – для (эквивалентной системы – 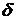 ). ). | (3.4) |
Очевидно, что для всех 3-х эквивалентных систем коэффициент 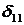 одинаков, так как все они построены на одной и той же основной системе.
одинаков, так как все они построены на одной и той же основной системе.
4. Для определения коэффициентов 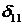 ,
, 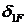 поочередно нагрузим основную систему единичной силой
поочередно нагрузим основную систему единичной силой 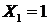 (рис. 3.4) и системой внешних сил (рис. 3.5) и получим величины продольных сил в стержнях.
(рис. 3.4) и системой внешних сил (рис. 3.5) и получим величины продольных сил в стержнях.
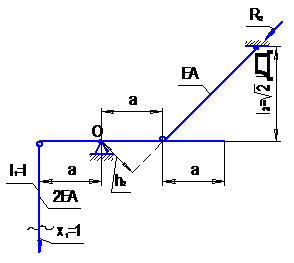 |
Рис. 3.4. Основная система, нагруженная 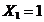 |
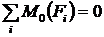
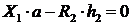
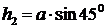 ;
;
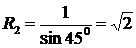 .
.
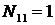 ;
;  – основание: метод сечений.
– основание: метод сечений.
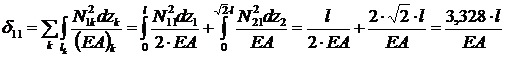 .
.
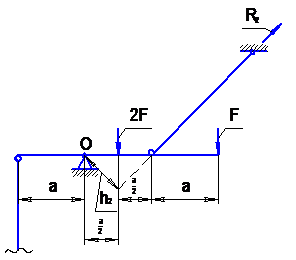 |
| Рис. 3.5. Основная система, нагруженная внешними силами |
В данном случае работает только стержень №2, в точке его крепления возникнет реакция 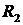 , которую определим из
, которую определим из 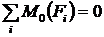 :
:
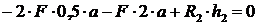
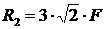 ;
;
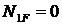 ;
; 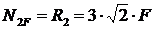 ;
;
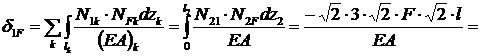
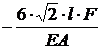
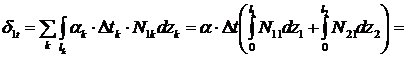
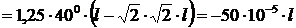 .
.
Решим каждое уравнение (1.2, 1.3, 1.4) относительно неизвестных 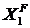 ,
, 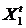 ,
, 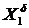 .
.
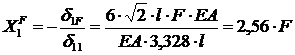 ;
;
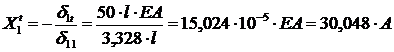 ;
;
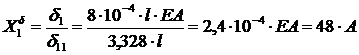 .
.
Каждое значение 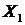 поставим на соответствующую эквивалентную систему (рис. 3.3 а, рис. 3.3 б, рис. 3.3 в) и определим для каждой эквивалентной системы реакцию в точке крепления второго стержня, используя уравнение равновесия
поставим на соответствующую эквивалентную систему (рис. 3.3 а, рис. 3.3 б, рис. 3.3 в) и определим для каждой эквивалентной системы реакцию в точке крепления второго стержня, используя уравнение равновесия 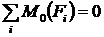 :
:
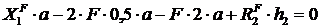 ;
; 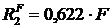
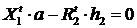 ;
; 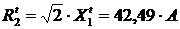
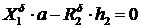 ;
; 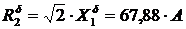
Определим напряжения в стержнях от каждого из факторов.
Продольные силы и напряжения в стержнях от силы 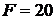 кН.
кН.
Так как 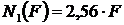 , а
, а 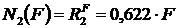 , то
, то
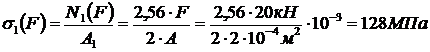 ;
;
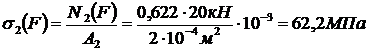 .
.
Продольные силы и температурные напряжения в стержнях при их равномерном нагреве на 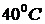 .
.
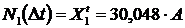 ;
;
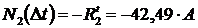 ;
;
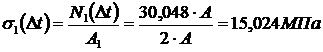 (стержень растянут);
(стержень растянут);
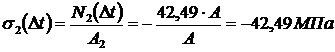 (стержень сжат).
(стержень сжат).
Продольные силы и сборочные напряжения в стержнях в результате неточности изготовления 1-го стержня (короче на 0,08% 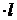 ).
).
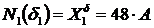 ;
;
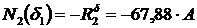 ;
;
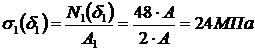 (стержень растянут);
(стержень растянут);
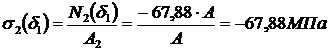 (стержень сжат).
(стержень сжат).
Суммарные продольные усилия и напряжения в стержнях от совокупности действия факторов.
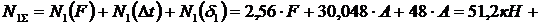
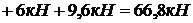 ;
;
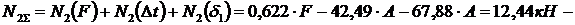
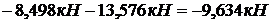 ;
;
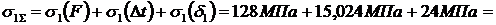
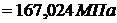 ;
;
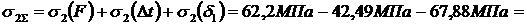
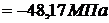 ;
;
Из результатов расчета видно, что в стержне №1 развиваются напряжения растяжения, превышающие допускаемую величину. Перегруз составляет 7,024 МПа, что в процентном соотношении от 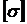 составляет:
составляет: 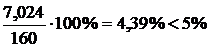 , то есть меньше допускаемого процента перегруза. Во втором стержне развивается напряжение сжатия за счет температурного воздействия и неточности изготовления, которые значительно меньше допускаемого. То есть в целом конструкция работоспособна при заданных условиях нагружения.
, то есть меньше допускаемого процента перегруза. Во втором стержне развивается напряжение сжатия за счет температурного воздействия и неточности изготовления, которые значительно меньше допускаемого. То есть в целом конструкция работоспособна при заданных условиях нагружения.
Основы теории колебаний
Удар
Ударом называется взаимодействие тел, при котором силы взаимодействия резко нарастают или ослабевают за короткий промежуток времени. Удар относится к динамическим видам нагружения.
Можно выделить три вида задач об ударе:
1. Задачи об изменении параметров движения взаимодействующих тел, решаемые аппаратом механики недеформируемого твердого тела.
2. Задачи о напряжениях и деформациях, возникающих во взаимодействующих телах, решаемые аппаратом механики деформируемого твердого тела.
3. Задачи об определении свойств материалов при ударе.
В курсе «Сопротивление материалов» решаются ударные задачи только второго вида: производится расчет на прочность и жесткость элементов конструкций при ударном нагружении. Более общий подход к решению таких задач был предложен доктором технических наук, основателем кафедры «Сопротивление материалов» Тольяттинского политехнического института Георгием Федоровичем Лепиным.
Теория удара Лепина
Основные допущения:
1. Ударяющее тело абсолютно жесткое.
2. Материал ударяемого тела следует закону Гука.
3. Ударяемое тело имеет одну степень свободы.
4. Удар неупругий, т.е. ударяющее тело после удара не отскакивает, а движется совместно с ударяемым телом.
5. Кинетическая энергия ударяющего тела полностью переходит в потенциальную энергию деформации ударяемого тела, т.е. можно пренебречь контактными явлениями.
6. Деформация мгновенно распространяется по ударяемой системе, и все ее точки начинают движение одновременно, т.е. можно пренебречь волновыми явлениями.
Рассмотрим упругую систему в виде пружины длиной l и жесткостью c с грузом весом F1. Пружина образует с горизонтом угол a и под действием веса груза имеет деформацию d. Абсолютно жесткое тело весом F движется со скоростью v под углом b к горизонту.
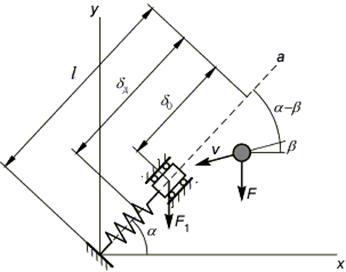
Определим перемещение упругой системы dд после удара (динамическое перемещение).
В соответствии с законом сохранения импульса, количество движения системы до и после удара одинаково. Проецируя количество движения на ось a, можно записать:
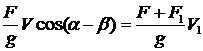 ,
,
где V1 – скорость движения системы после соударения:
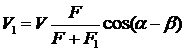 . (4.1)
. (4.1)
Воспользуемся теоремой о кинетической энергии:
T2 – T1 = I, (4.2)
где T1, T2 – кинетическая энергия в начале и конце ударного взаимодействия соответственно, I - работа всех сил на перемещении во время ударного взаимодействия.
Кинетическая энергия системы в начале взаимодействия равна
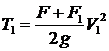 .
.
Подставляя сюда вместо V1 выражение (11.1), получим:
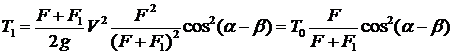 , (4.3)
, (4.3)
где 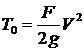 – кинетическая энергия ударяющего тела.
– кинетическая энергия ударяющего тела.
В конце ударного взаимодействия система неподвижна, и ее кинетическая энергия T2=0.
Работа внешних сил складывается из работы силы тяжести и силы упругости пружины:
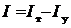 .
.
Работа силы тяжести системы на перемещении, вызванном ударом:
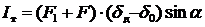 . (4.4)
. (4.4)
Рассмотрим зависимость силы упругости Fу от перемещения d. По закону Гука 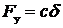 :
:
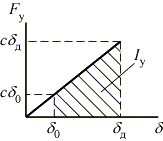
Как видно из графика, работа силы упругости на перемещении, вызванном ударом, определяется
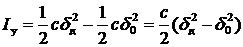 .
.
Представим жесткость пружины в виде 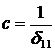 , где d11 – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости
, где d11 – податливость упругой системы (перемещение точки соударения под действием единичной силы, приложенной по направлению перемещения во время ударного взаимодействия). Тогда работа сил упругости
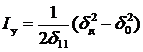 . (4.5)
. (4.5)
Формула (11.2) с учетом выражений (11.3), (11.4) и (11.5) принимает вид:
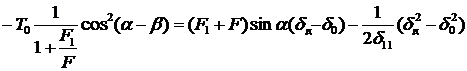 ,
,
откуда
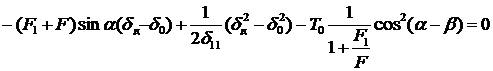 ,
,
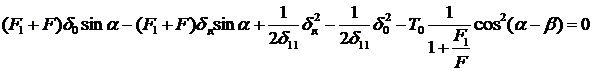 ,
,
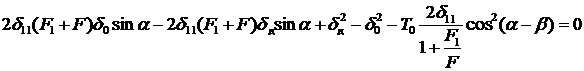 .
.
Учитывая, что 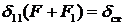 – статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):
– статическое перемещение (перемещение точки соударения под действием силы тяжести взаимодействующих тел, приложенной статически по направлению перемещения во время ударного взаимодействия):
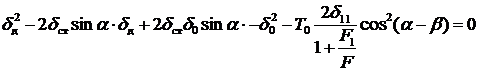 .
.
Поскольку корни квадратного уравнения вида 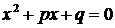 равны
равны 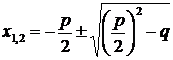 , то
, то
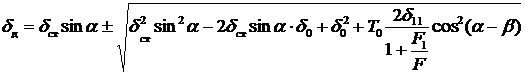 ,
,
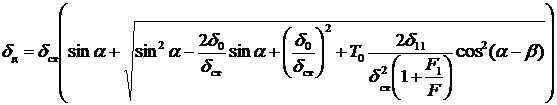 .
.
Таким образом, перемещение при ударе вычисляется по формуле:
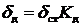 , (4.6)
, (4.6)
где Kд – коэффициент динамичности:
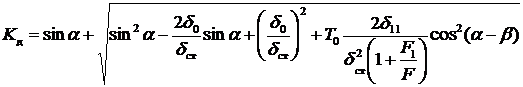 (4.7)
(4.7)
В области упругих деформаций напряжение, возникающее при ударе
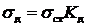 . (4.8)
. (4.8)
Частные случаи удара
1. Тело массой m падает н
