И наименьшее значение функций на промежутке

Всюду далее функция 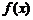определена на рассматриваемых промежутках.

Теорема 1. Дифференцируемая на 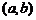функция (убывает) на этом интервале тогда и только тогда, когда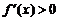

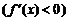
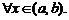
Точка 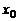называется точкой локального максимума (минимума) функции 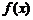, если существует некоторая окрестность точки 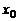такая, что для всех x из этой окрестности выполняется неравенство .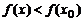

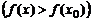Значение 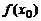называется локальным максимумом (минимумом) функции.

Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.

Теорема 2 (необходимое условие существования экстремума функции).

Если в точке 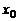функция 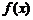достигает экстремума, то ее производная в этой точке равна нулю или не существует. Точки, в которых производная функции 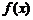обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того, чтобы определить точки экстремума используют достаточные условия (признаки экстремума).

Теорема 3 (первый признак экстремума функции).

Пусть 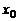– критическая точка непрерывной функции .

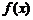Если в некоторой окрестности точки 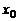выполняется условие

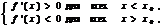
то 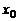– точка локального максимума;

если выполняется условие

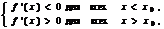
то 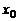– точка локального минимума.

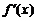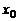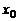Если производная имеет один и тот же знак в левой и правой полуокрестности точки , то не является точкой экстремума.

Теорема 4 (второй признак экстремума функции).

Пусть 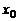– критическая точка функции 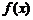, дважды дифференцируемой в окрестности точки 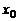. Тогда 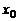является точкой локального минимума функции 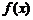, если 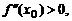и точкой локального максимума, если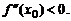

Теорема 5 (третий признак экстремума функции).

Пусть 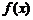– n раз непрерывно дифференцируемая в критической точке 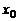функция и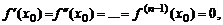 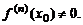Тогда:

1) если n – четное и 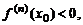то 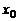– точка локального максимума;

2) если n – четное и 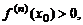то 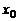– точка локального минимума;

3) если n – не четное, то 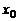не является точкой локального экстремума.

Точка 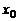называется точкой глобального максимума (минимума) функции 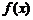на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство .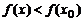

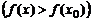Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).

Теорема 5 (Вейерштрасса). Если функция 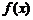непрерывна на отрезке 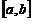, то она достигает на нем своих наименьшего и наибольшего значений

Непрерывная на отрезке 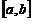достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.

Для отыскания глобальных экстремумов функции 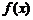на отрезке 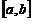необходимо:

1) найти производную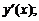

2) найти критические точки функции;

3) найти значения функции на концах отрезка, т. е. 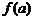и 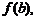а также в критических точках, принадлежащих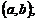

4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.

График функции 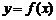называется вогнутым (выпуклым вниз) на 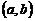, если дуга кривой 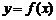на этом интервале расположена выше любой касательной проведенной к графику этой функции (рис. 1).

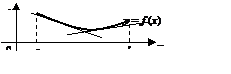
Рис. 1.

График функции 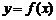называется выпуклым (выпуклым вверх) на 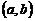, если дуга кривой 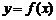на этом интервале расположена ниже любой касательной проведенной к графику этой функции (рис. 2).

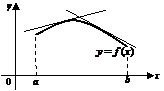
Рис. 2.

Теорема 6. Если функция 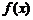дважды дифференцируема на 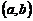и 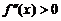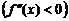всюду на этом интервале, то график функции вогнут (выпуклый) на .

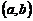Точка 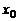така, что график функции 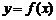меняет выпуклость на вогнутость или наоборот, проходя через 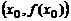, называется точкой перегиба (рис. 3)

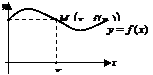
Рис. 3.

Для нахождения точек перегиба вначале находят критические точки 2-го рода – те значения x, для которых 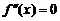или 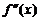не существует. Далее используют достаточные условия перегиба.

Теорема 7 (достаточные условия перегиба).

Если для функции 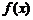вторая производная 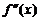в некоторой точке 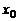обращается в нуль или не существует и при переходе через нее 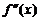меняет свой знак, то 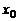– точка перегиба.

План исследования функции и построения графика

1. Найти область определения 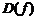функции .

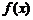2. Найти область значений 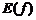(если это возможно вначале, часто 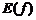можно указать только по результатам исследования).

3. Исследовать функцию на четность.

4. исследовать на периодичность.

5. Найти точки пересечения с осями Ox (нули функции) и Oy.

6. Найти промежутки знакопостоянства функции.

7. Исследовать на непрерывность, дать классификацию разрывов.

8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).

9. Исследовать на монотонность и экстремум.

10. Исследовать на выпуклость, вогнутость, перегиб.

11. Построить график функции.