Частные производные 1 и 2 порядка функции двух переменных.
Пусть задана функция 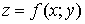 . Так как x и y – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной x приращение
. Так как x и y – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной x приращение 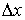 , сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается
, сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается 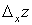 . Итак,
. Итак, 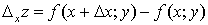 .
.
Аналогично получаем частное приращение z по y: 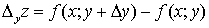 .
.
Полное приращение 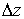 функции z определяется равенством
функции z определяется равенством 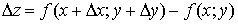 .
.
Если существует предел 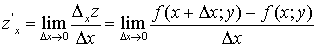 , то он называется частной производной функции
, то он называется частной производной функции 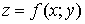 в точке
в точке 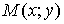 по переменной x и обозначается одним из символов:
по переменной x и обозначается одним из символов:
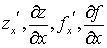 .
.
Частные производные по x в точке 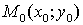 обычно обозначают символами
обычно обозначают символами 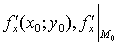 .
.
Аналогично определяется и обозначается частная производная от 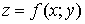 по переменной y:
по переменной y:
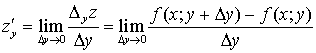
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции 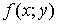 находится по формулам и правилам вычисления производных функции одной переменной (при этом соответственно x или y считаются постоянной величиной).
находится по формулам и правилам вычисления производных функции одной переменной (при этом соответственно x или y считаются постоянной величиной).
Частные производные 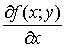 и
и 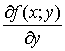 называют частными производными первого порядка. Их можно рассматривать как функции от
называют частными производными первого порядка. Их можно рассматривать как функции от 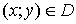 . Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
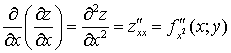 ;
; 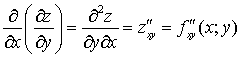 ;
;
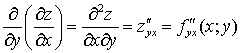 ;
; 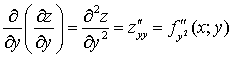 .
.
Дифференциалы 1 и 2 порядка функции двух переменных.
Полный дифференциал функции (формула 2.5) называют дифференциалом первого порядка.
Формула для вычисления полного дифференциала имеет следующий вид:
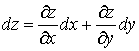 (2.5) или
(2.5) или 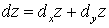 , где
, где 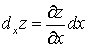 ,
, 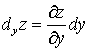
частные дифференциалы функции 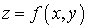 .
.
Пусть функция 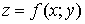 имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле
имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле 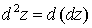 . Найдем его:
. Найдем его:
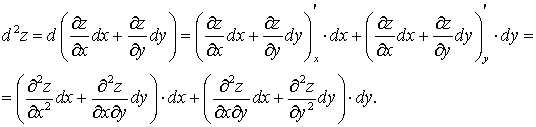
Отсюда: 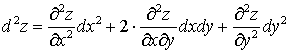 . Символически это записывается так:
. Символически это записывается так:
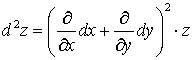 .
.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Первообразная функции, неопределенный интеграл, свойства.
Функция F(x) называется первообразной для данной функции f{x), если F'(x)=f(x), или, что то же, если dF(x)=f(x)dx.
Теорема. Если функция f(x), определенная в некотором промежутке (X) конечной или бесконечной длины, имеет одну первообразную, F(x), то она имеет и бесконечно много первообразных; все они содержатся в выражении F(x)+С, где С — произвольная постоянная.
Совокупность всех первообразных для данной функции f(x), определенной в некотором промежутке или на некотором отрезке конечной или бесконечной длины, называется неопределенным интегралом от функции f(x) [или от выражения f(x)dx ] и обозначается символом  .
.
Если F(x) есть одна из первообразных для f(x), то согласно теореме о первообразных
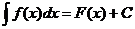 , где С есть произвольная постоянная.
, где С есть произвольная постоянная.
По определению первообразной F'(x)=f(x) и, следовательно, dF(x)=f(x) dx. В формуле (7.1), f(x) называется подинтегральной функцией, а f(x) dx — подинтегральным выражением.
