Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx

Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

Теорема Ролля. Лагранжа. Коши

Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.

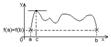
Теорема Лагранжа.

Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.

т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).

Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.

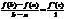
Теорема Коши.

Если f(x), g(x) удовл. трем условиям:

1). f(x), g(x) непрерыв. на промеж [a,b]

2). f(x), g(x) деффер. на интервале (a,b)

3). g’(x)¹0 на интер. (a,b), то сущ. т. с

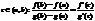
g(b)¹g(a) (неравны по теореме Ролля).

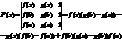
1). F(x) – непрерывна на [a,b]

2). F(x) – деффиренцирована на (a,b)

3). F(a)=0 ; F(b)=0

по теореме Ролля сущ. сÎ(a,b); F’(с)=0

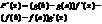
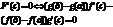
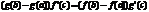
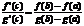
Производная ф-и задана неявно

Функция z=f(x,y) наз. Заданной неявно, если она определена равенством, неразрешенным относительно z .F(x,y,z)=0 x+y+z=e^z - это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде.x²+y²+z²=0 - не задает никакой функции. Теорема: Если ф-я F(x,y,z) - непрерывна в т. р₀(x₀,y₀,z₀) и ее производная по z F_z(x,y,z)¹0, то равенство F(x,y,z)=0 однозначно определяет в неявном виде функцию z=f(x,y), при этом эта функция дифференцируема и ее производная находится по формулам: ¶z/¶x=- F¢_x(x,y,z)/F¢_z(x,y,z) ¶z/¶y=-F¢_z (x,y,z)/F¢_y(x,y,z)Док-во: Найдем полный дифференциал функции dF(x,y,z)=¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz F(x₀,y₀,z₀)=0èdF=0è¶F/¶x*dx+¶F/¶y*dy+¶F/¶x*dz=0 dz=-(¶F/¶x)/(¶F/¶z)*dx-(¶F/¶y)/(¶F/¶z)*dy (*) С другой стороны: z=f(x,y), dz=¶z/¶x*dx+¶z/¶y*dy (**) Сравнивая (*) и(**) è¶z/¶x=- F¢_x(x,y,z)/F¢_z(x,y,z)¶z/¶y=-F¢_z (x,y,z)/F¢_y(x,y,z)

16.4. Экстремумы функции. Необходимое условие экстремума (теорема Ферма).

Точка х называется точкой max ф-ции, если значение ф-ции в этой точке - наименьшее в некоторой ее окрестности.

1- локальный max

2- локальный min

3- глобальный max

4- глобальный min

если tga>0, то f`(x)>0

если tga<0, то f`(x)<0

Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.

(В них можно построить ¥ касательных).

Достаточный признак: точка х₀ является точкой экстремума, если ее производная в этой точке меняет знак:

- если с “+” на “-”, то х₀- т. max

- если с “-” на “+”, то х₀- т. min

Асимптоты.

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

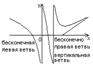
Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

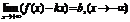
Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

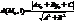
Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

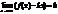существует предел: