Предел функции, его геометрическая интерпретация, действия над пределами.

Рассмотрим числовое множество 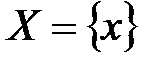. Точка «a» называется точкой сгущения этого множества, если в любой близости от a содержатся значения x из X отличные от a.

Или: введем понятие окрестности точки а: так называется любой открытый промежуток с центром в точке а. Теперь можно сказать, что точка «а» будет точкой сгущения множества x , если в каждой ее окрестности содержатся отличные от а значения x из X.

Пусть в области x, для которой точка а является точкой сгущения, задана некоторая функция f(x). Представляет интерес поведение этой функции при приближении «x» к «а».

Число А называется пределом функции y=f(x) при x стремящемся к а, если для любого e>0 существует число d(e)>0 такое, что при ½x-a½<d(e) выполняем неравенство ½f(x)-A½<e.

В этом случае пишут 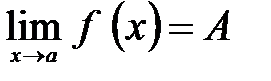(1)

Если область x такова, что в любой близости от а, но справа от а, найдутся отличия от а значение x из x (в этом случае точку а называют правой точкой сгущения), то можно дать определение предела функции, ограничиваясь лишь значением x>a. В этом случае предел функции называется пределом функции f(x) при стремлении x к а справа.

Число А называется правосторонним пределом или пределом справа функции f(x) в точке x=a если для "e>0 $ d(e)>0, что при 0<x-a<d(e) выполняется неравенство ½f(x)-A½<e. Пишут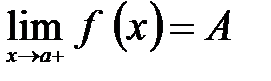

Число А называется левосторонним пределом или пределом слева функции f(x) в точках x=a, если для любого e>0 $ d(e)>0, что при 0<а-x<d(e) выполняется неравенство ½f(x)-A½<e. Пишут .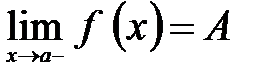

Число А называется пределом функции y=f(x) при x®¥ если для "e>0 существует число M(e)>0 такое что при ½x½> M(e) выполняется неравенство ½f(x)-A½<e, пишут.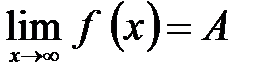

Предел функции в некотором смысле может быть сведен к пределу последовательности.

Пусть множества x={x} имеет точку сгущения а (а - конечна или бесконечна). Тогда из x (бесконечным множеством способов) можно извлечь, такую последовательность x1 , x2 , xn … (2) значений x (отличных от а) которая имела бы своим пределом а.

Последовательности (2) соответствует последовательность значений функций f(x1), f(x2) …f(xn) (3)

При условии равенства (1) эта последовательность всегда имеет предел А (без доказательства).

Получим второе определение предела функции. для любой последовательности (2), имеющей пределом а, соответствует последовательность (3), имеющая предел А.

Действия над пределами.

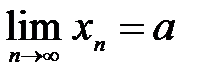
1. Если {xn} и {yn} имеют конечные пределы 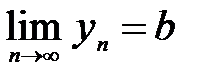, то и сумма (разность) их также имеет конечный предел,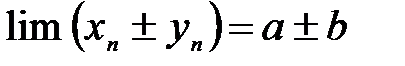

2. Если {xn} и {yn} имеют конечные пределы: 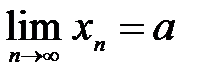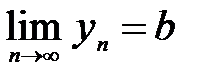, то их произведение также имеют конечный предел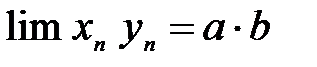

3. Если {xn} и {yn} имеют конечные пределы: 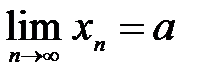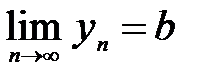причем b¹0, то их отношение также имеет конечный предел .

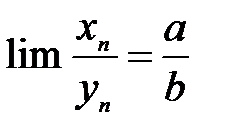Первый и второй замечательный предел

Теорема. 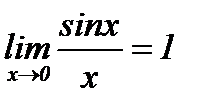(раскрывает неопределенность типа 0/0).

Второй замечательный предел 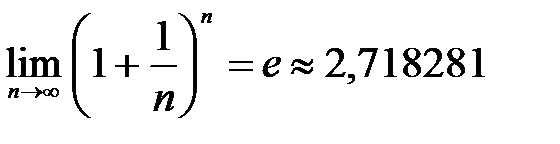- иррациональное число.