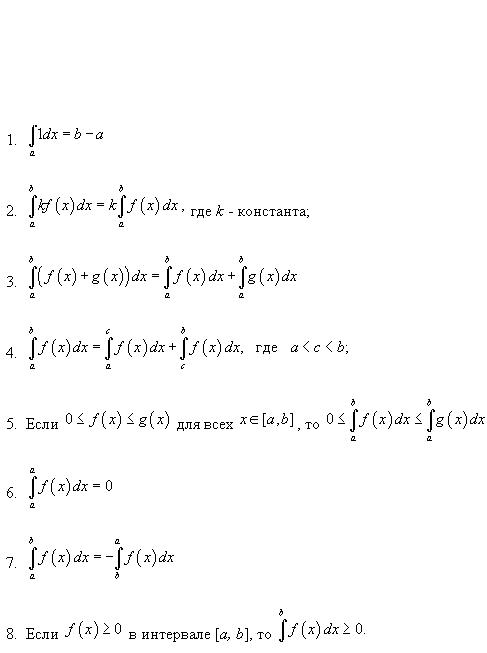Наибольшее и наименьшее значения ф.м.п. в ограниченной замкнутой области.

Пусть функция z=f(x;y) определена и непрерывна в ограничен­ной замкнутой области D (над D черточка). Тогда она достигает в некоторых точках D своего наибольшего М и наименьшего m значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области D(над D черточка), или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений диф­ференцируемой в области D (над D черточка) функции z=f(x;y) состоит в следующем:

1. Найти все критические точки функции, принадлежащие D(над D черточка) и вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции z=f(x;y) на границах области;

3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее m

Постановка задачи нахождения условного экстремума ф.м.п.

Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в замкнутой области.Найти экстремум z, при ксловии, что x и y связаны следующим образом.

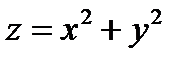; x+y-1=0;

(*)

; ; ;

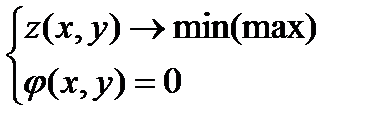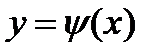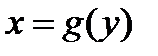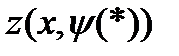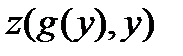
Метод множителя Ла-Гранджа.

(*) эквивалентна задаче: 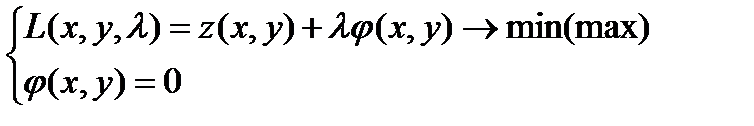, где

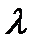-множитель Ла-Гранджа; 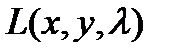- функция Ла-Гранджа.

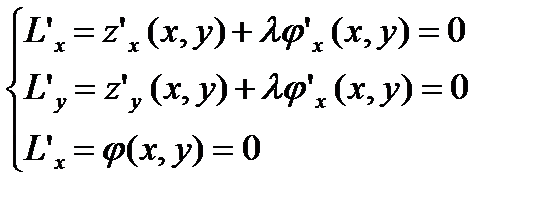
Надо исследовать 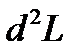ф-ции Ла-Гранджа с учетом условия связи в диффиринциалах.

Наибольшее и наименьшее значение ф-ции в замкнутой области.

Если ф-я определена в замкнутой ограниченной области Д, то она достигает своего min и max значения, либо в стационарных точках внутри области, либо на ее границе.

25. Опред опред интеграла \. Геом и физич интерпретация опред интеграла

Это — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Пусть на отрезке [a,b] задана функ y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим 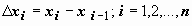макс из длин отрезков обозначим 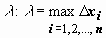На каждом из отрезков [xi-1 , xi] выберем произвольную точку и составим

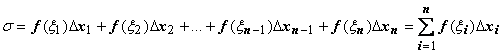
Сумма 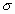наз интегральной суммой. Если сущ-т (конечный) предел последов-ти интеграл сумм 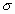при 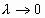не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек , то функция f(x) наз-ся интегрир. по отрезку [a,b], а этот предел наз-ся определ. Интегр. от функ. f(x) по отрез. [a,b] и обозначается 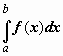это есть опред интеграл

Геометрический смысл

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Услов интегрируемости функ. Форм. Нюьтона-Лейбница

Определенный и неопределенный интегралы связывает основная теорема интегрального исчисления:

Теорема 2. Если функция f(x) интегрируема на отрезке [a, b] и имеет на нем первообразную, то для любой ее первообразной F(x) на этом отрезке справедлива формула

Фолрмула Ньютона-Лейбница

Формула Ньютона — Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определ. интеграла и вычислением первообразной.

Если 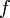непрерывна на отрезке 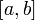и 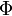— ее любая первообразная на этом отрезке, то имеет место равенство

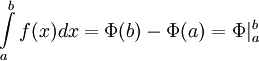
27. Свойства определенного интеграла