Условия возрастание и убывание функции.
Функция называется возрастающей (убывающей) в некотором промежутке, если в этом промежутке каждому большему значению аргумента соответствует большее (меньшее) значение функции.возрастающие, так и убывающие функции, называются монотонными. Возрастание и убывание функции y = f{x) определяется знаком ее производной: если в некотором интервале f'(x) > 0, то функция возрастает, а если f'(x)< 0, то функция убывает в этом интервале.
Первое правило нахождения экстремумов функции f(x) (по первой производной):
· Находим область определения функции D(f)•
· Ищем первую производную функции f '(x).
· Находим критические точки первой производной.
· Определяем знак производной f '(x).слева и справа от критической точки, в которой функция непрерывна. Если знак изменяется с плюса на минус, то в данной точке функция имеет максимум, если с минуса на плюс, то - минимум. Если же знак производной не изменяется, то в данной точке экстремума нет.
Второе правило нахождения точек экстремума (по второй производной):
· Находим область определения функции D(f).
· Ищем первую производную функции f '(x)
· Находим точки, в которых f '(x) = 0, а функция f(х) непрерывна.
· Ищем вторую производную f "(x)
· Во вторую производную f "(x) подставляем каждое из значений, полученных в п. 3. Если f "(хо)>0; то в точке х0 функция имеет минимум, если f "(хо)<0, то - максимум. Если f ”(хо) = 0, то вопрос о наличии экстремума остается открытым (можно воспользоваться первым правилом).
Выпуклость и вогнутость кривой. Точки перегиба
Кривая называется выпуклом (вогнутой) в некотором промежутке , если она расположена ниже (выше) касательной , проведенной к кривой в любой точке этого промежутка . Выпуклость или вогнутость кривой, являющейся графиком функции у = f(x).Характеризуется знаком второй производной f“(x) > 0 , а именно: если в некотором промежутке f “(х)>О, то кривая вогнута, если f “(х)<0, то кривая выпуклав этом промежутке.Следовательно, нахождение промежутков выпуклости и вогнутости график функции у=… сводится к нахождению промежутковзнакопостоянства ее второй производной f ‘’(х).
Точкой перегиба кривой называется такая ее точка , которая отделяет участок выпуклости от участка вогнутости.
Точками перегиба графика функции y = f(х) могут быть только точки, в которых вторая производная изменяет свой знак.т.е. точки, находящиеся внутри области определения функцииf(x)в которых вторая производнаяf ‘’(х) обращается в нуль или терпит разрыв. Такие точки называются критическими точками второй производной.
Точками перегиба графика функцииу= f(х) будут лишь те критические точки второй производной, при переходе через которые f ‘’(x)меняет знак.
Отсюда полу чаем правило нахождения промежутков выпуклости и вогнутости и точек перегиба графика функции:
1)Находим область определении функцииD(f).
2) Ищем 2-ую производную функцииff (x).
3) Определяем точки, вкоторых вторая производная f ‘’(x)оброщается в нуль или терпитразрыв (критические точки 2-ой производной)|4)Находим промежутки, на которые разбивают области определенияD(f) критические точки.5)Определяем знак f ‘’(x) на каждом из полученных промежутков: если f‘’(x)> о, то это промежуток вогнутости; если жеf’’(x)< О, то это промежуток выпуклости.
6)Те из граничных точек промежутков, в которых функции f(x) непрерывна, а вторая производная f’’(x) изменяет свой знак при переходе через них, являются точками перегиба:
При нахождении интервалов выпуклости и вогнутости и точек перегиба удобно результаты исследования записывать и таблицу изменения знаков второй производной.
Асимптоты
Асимптотой кривой называется прямая , к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат.
Различают вертикальные и наклонные асимптоты.
Прямая X=a является вертикальной асимптотой графики функции y=f(x) , если , по крайней мере , один из односторонних пределов в точке .x=a равен бесконечности т.е.
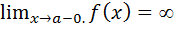 или
или 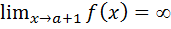
Прямаяy=k1x+b1 является наклонной асимптотой при x->+∞ если существуют оба предела
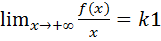 и b1=
и b1= 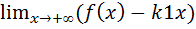
Аналогично, если существуют пределы
K1= 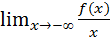 и b1=
и b1= 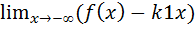
То прямаяy=k2x+b2 является наклонной асимптотой приx->-∞
Если k=0 и существует 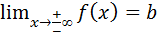 , то получаем горизонтальную асимптоту y=bкак частный случай наклонной.
, то получаем горизонтальную асимптоту y=bкак частный случай наклонной.
Если вертикальных асимптот может быть любое число , то наклонных асимптот не может быть более 2-ух.
