Классификация точек разрыва.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел 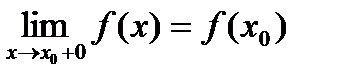, то функция называется непрерывной справа.

Если односторонний предел 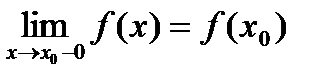, то функция называется непрерывной слева.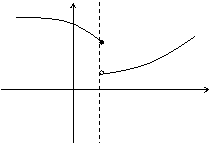

Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.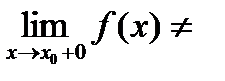

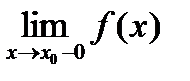
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.

Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

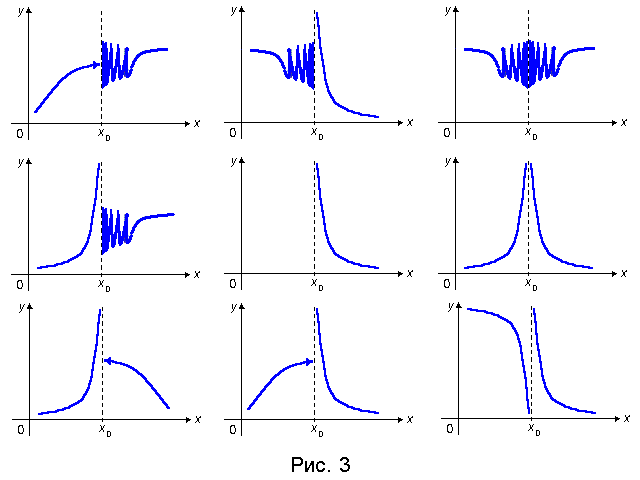
Если значения на концах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке , то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.

89. Производная. Определение. Механический и геометрический смысл производной.

Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.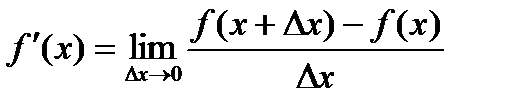

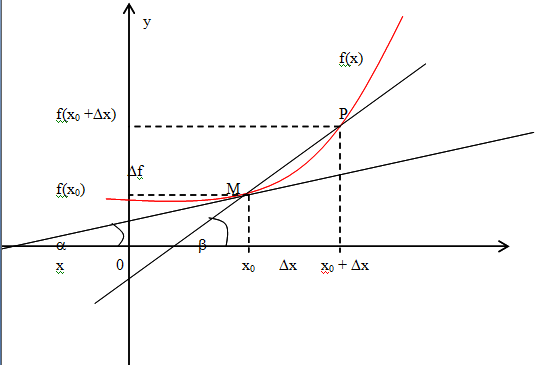
Пусть f(x)определена на некотором промежутке (a, b). Тогда 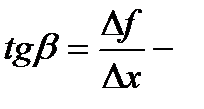тангенс угла наклона секущей МР к графику функции.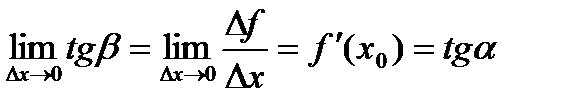

где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: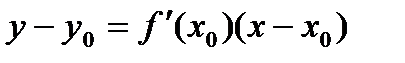

Уравнение нормали к кривой: .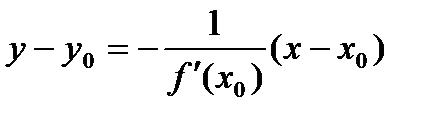

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

90. Дифференцируемость функции. Определение. Теорема о непрерывности дифференцируемой функции.

Теорема о непрерывности дифференцируемой функции.Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0. Если функция дифференцируема в некоторой точке a, то она непрерывна в этой точке. По определению производнойЭто предельное равенство означает, что выражение под знаком предела можно представить в видегде α(x) – бесконечно малая функция при x → a. Тогда Следовательно, при x → a.

91. Основные правила дифференцируемости.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1) (u ± v)¢ = u¢± v¢

2) (u×v)¢ = u×v¢ + u¢×v

3) 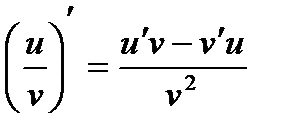, если v¹ 0

Эти правила могут быть легко доказаны на основе теорем о пределах.

92. Производная сложной функции.

Теорема.Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда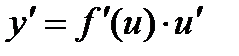

Доказательство.

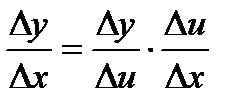
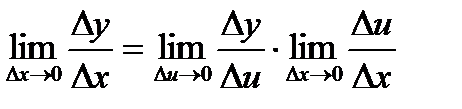
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)

Тогда 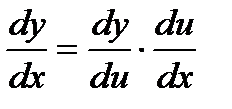. Теорема доказана.