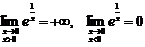Предел функции в точке. Основные теоремы о пределах.

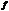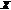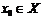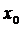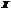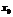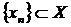Рассмотрим функцию , определенную на множестве . Пусть . Точка называется предельной или точкой сгущения множества , если в любой окрестности этой точки найдутся точки множества, отличные от . В этом случае из множества можно выделить последовательность , сходящуюся к 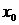. К числу предельных точек можно отнести внутренние точки множества, входящие в состав 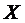вместе с некоторой окрестностью. Очевидно, что в общем случае точка сгущения может оказаться не внутренней. В качестве примера можно привести множество рациональных чисел 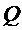, все точки которого в любой окрестности содержат кроме рациональных чисел и иррациональные, которые в 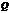не входят.

Множество 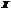называется замкнутым, если оно содержит все свои предельные точки, и множество 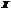называется открытым, если оно состоит из одних внутренних точек.

Функция 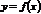, определенная на множестве имеет предел 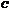в точке сгущения 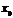: если для любого 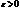найдется такое 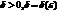, что при .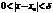

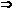
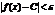Указанное определение опирается на понятие функции и именуется определением предела по Коши.

Теорема 1. (о представлении суммы в виде суммы своего предела и бесконечно малой функции). lim _х→af(x) = A тогда и только тогда, когда f(x) = A + α(x), где α(x) – бесконечно малая функция при х→a.

Теорема 2. (о пределах суммы, произведения и частного). Если функция f(x) u g(x) определены в некоторой окрестности точки а, возможно, за исключением самой точки а, и существуют пределы lim _х→af(x), lim _х→ag(x), то существуют пределы и суммы lim _х→a(f(x) + g(x)), произведения lim _х→a(f(x)g(x)) и, если g(x) ≠ 0, то и частного lim_x→xf(x)/g(x) и имеют место равенства

d) lim_x→a(f(x) + g(x)) = lim_x→af(x) + lim_x→ag(x);

e) lim_x→a(f(x)g(x)) = lim_x→af(x) * lim_x→ag(x);

f) lim_x→af(x)/g(x) = l im_x→af(x)/lim_x→ag(x), при g(x) ≠ 0 u lim_x→ag(x) ≠ 0.

Следствия:

4) постоянный множитель может быть вынесен из-под знака предела.

lim_x→acf(x) = lim_x→ac lim_x→af(x) = c lim_x→af(x)

5) предел разности равен степени пределов

lim_x→a (f(x) - g(x)) = lim_x→a(f(x) + (-1)g(x)) = lim_x→af(x) + lim_x→a(-1)g(x) = lim_x→af(x) + (-1)lim_x→ag(x) = lim_x→af(x) - lim_x→ag(x)

6) предел степени равенстепени предела

если показатель степени n?N, то lim_x→a(f(x))ⁿ = lim_x→af₁(x) * f₂(x) * …… * f_n(x) = lim_x→af₁(x) * lim_x→af₂(x) * …. * lim_x→af_n(x) = (lim_x→af(x))ⁿ

Теорема 3 (о пределах промежуточной функции). Если lim_x→af(x) = A, lim_x→af(x0 = A и в некоторой окрестности точка а (быть может, кроме точки а) имеют место неравенства f(x) ≤ ф ≤ g(x), To lim_x→aф(x)=A.

Замечательные пределы, односторонние пределы.

Односторонние пределы

В определении предела функции предполагалось, что 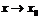произвольным образом. Если при вычислении предела функци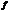и при 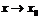считать, что 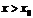, то получают односторонний предел справа или правосторонний предел функции в точке 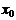. Если же считать, что 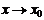и 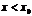, то получаютодносторонний предел слева или левосторонний предел.

Так, например, односторонние пределы функции 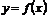, изображенной на Рис. 2, соответственно, равны: 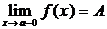и .

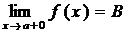Правосторонний предел обозначают символом 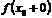, левосторонний ‑ символом 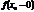. Таким образом:

.

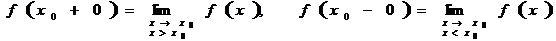В этих определениях предполагается, что функция определена на некотором промежутке соответственно справа или слева от точки сгущения .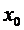

Для того, чтобы у функции 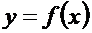в точке 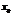существовал двусторонний предел 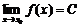, необходимо и достаточно, чтобы существовали левосторонний и правосторонний пределы 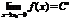и 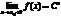функции 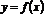в точке 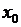, и эти пределы были равны между собой: .

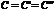Пример.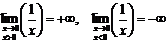

Пример.