Определите понятие абсолютной и относительной погрешности. Сформулируйте теоремы о погрешности суммы, разности, произведения, частного, степени и корня. Изложите правила округления.

Абсолютная погрешность измерения - разность между результатом измерения Х и истинным значением Хo измеряемой величины: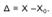

Относительная погрешность измерения - отношение абсолютной погрешности измерения к истинному значению измеряемой величины Хo: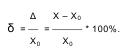

Погрешность суммы

Абсолютная погрешность суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел.

|Δu|<=|Δx1|+|Δx2|+...+|Δxn|

Следствие: За предельную абсолютную погрешность алгебраической суммы можно принять сумму предельных абсолютных погрешностей.

Δu=Δx1+Δx2+...+Δxn

Если слагаемые - одного и того же знака, тот предельная относительная погрешность их суммы не превышает наибольшей из предельных относительных погрешностей слагаемых.

δu<=max(δx1,δx2,...,δxn)

Погрешность разности

Предельная абсолютная погрешность разности равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого

Δu=Δx1+Δx2

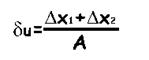
Погрешность произведения

Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышают суммы относительных погрешностей этих чисел.

δ<=δ1+δ2+...+δn

Погрешность частного

Относительная погрешность частного не превышает суммы относительного погрешностей делимого и делителя.

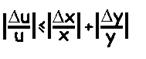
Погрешность степени

Предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа.

δu=m·δx

Относительная погрешность корня

Предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа.

δu=(1/m)·δx

При округлении числа мы заменяем его приближенным с меньшим количеством значащих чисел. В результате чего возникает погрешность округления; чтобы она была минимальной, нужно придерживаться правил округления.

1. Если первая из отбрасываемых цифр больше 5, то последняя из сохраняемых цифр увеличивается на 1.

4,57=4,6 0,6973=0,70

2. Увеличение на 1 и тогда, когда первая их отбрасываемых цифр равна 5, а за ней следует отличная от 0 цифра.

0,651=0,7 4,7756=4,78

3. Если первая из отбрасываемых цифр меньше 5, то последнее из сохраняемых остается без изменения.

0,6437=0,6 3,77532=3,775

4. Если первое из отбрасываемых цифр равно 5, а за ней не следуют оотличные от 0 цифры, то последнее из сохраняемых увеличивается на 1, если она нечетная, и остается без изменения, если четная.

5,575=5,58 5,585=5,58

Таким образом при использовании правил округления получается, что абсолютная погрешность округлений не превосходит половины единицы разряда определяемого последней оставленной значащей цифрой.

57 бИЛЕТ
Сформулируйте задачу интерполирования функций, изложите математическую постановку задачи интерполирования, определите понятие интерполяционного многочлена Лагранжа.

Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x1,x2,...,xn+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:

(xk)=yk, k=1,2,...,n+1,

где yk - известные значения функции ƒ(x) в точках xk. Функция g(x) называется интерполянтом функции ƒ(x).

В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций оказывается эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.

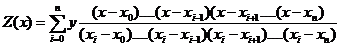интерполяционный многочлен Лагранжа

БИЛЕТ