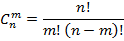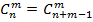Определение определенного интеграла. Геометрическая интерпритация определенного интеграла.

Пусть ф-ция f(x) непрерывна на отрезке ав. Разобьем отрехок ав произвольным образом на n частей, точками a=x0<x1<x2<…<xn=b.

∆i=xi-xi-1 ∆i- длина отрезка – (xi;xi-1)

[xi;xi-1] принадлежит ξi, i=1,2,…,n

Предположим, что существует предел конечный Sn, при условии, что n стремится к бесконечности, а максимальная длина стремится к 0.

Limn-∞Sn= Limn-∞∑f(ξi)∆i=⌠f(x)dx

, тогда он называется определенным интегралом ф-ции f(x) по отрезку ав и читается следующим образом: интеграл от а до b, f(x) до ч, чмсло а и в- пределы интегрирования.

Геометрический смысл определенного интеграла, если f(x)>0, на отрезке ав, то определенный интеграл численно равен площади криволинейной трапеции, ограниченной снизу осью х, сверху графиком ф-ции f(x) слева- прямой х=а, справа- х=в

Свойства определенного интеграла

1)а

⌠f(x0dx=0

b

2) a a

⌠f(x)dx=-⌠f(x)dx

b b

3) b b b

⌠(f(x)+g(x))dx=⌠f(x)dx+⌠g(x)dx

a a a

4)a a

⌠αf(x)dx=α⌠f(x)dx

b b

5)a c b

⌠f(x)dx=⌠f(x)dx+⌠f(x)dx

b a c b

6)m≤f(x)≤M: любое х принадлежит отрезку ав. m(b-a)≤ ⌠f(x)dx≤M(b-a)

A

7)f(x)непрерывна на отрезке ав, (то)=>существует с принадлежащая отрезку ав

b

⌠f(x)dx=f(c)*(b-a)

A

Формула Ньютона-Лейбница

Если 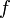непрерывна на отрезке 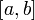и 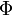— ее любая первообразная на этом отрезке, то имеет место равенство

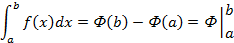
Замена переменной в определенном интеграле

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t 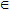[α,β].

Тогда справедливо следующее равенство:

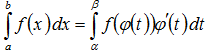
Эта формула носит название формулы замены переменной в определенном интеграле.

Интегрирование по частям в определенном интеграле

Интегри́рование по частя́м -Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией),

Если u(x), v(x) - непрерывно дифференцируемые функции, то .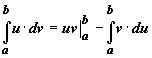

Дифференциальные уравнения. Задача Коши

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Дифференциальное уравнение с разделяющимися переменными

В качестве дифференциальных уравнений с разделяющимися переменными принято определять ОДУ первого порядка, приводящиеся к виду 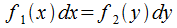(ДУ с разделенными переменными).

Запишем такие уравнения:

а)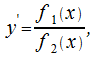

б)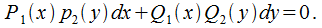

Линейное ДУ первого порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

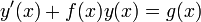
Формулы комбинаторики

· Размещение:

Размещение из n по m элементам называется любая упорядоченная выборка содержащая m-элементов.

Любые 2 размещения считаются различными, если они отличаются друг от друга составом или порядком следования элементов.

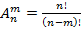
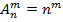
· Перестановка:

Перестановкой из n-элементов называется размещение из n по m.

2 любые перестановки отличаются только порядком следования элементов.

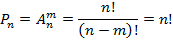
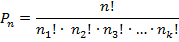
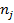- количество повторений j-ого элемента.

· Сочетание:

Сочетание из n-элементов по m-элементам называется любое подмножество одного множества. Два любых элемента отличаются друг от друга хотя бы элементом.