Линейные однородные уравнения с постоянными коэффициентами.
Линейное однородное уравнение 2-ого порядка
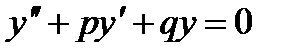 (1)
(1)
p, q — постоянные действительные числа
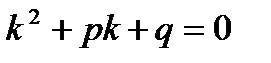 (2) характеристическое уравнение, его корни
(2) характеристическое уравнение, его корни
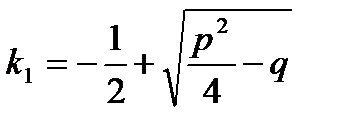 ,
, 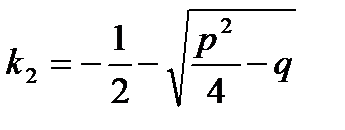
При этом возможны следующие случаи:
1. 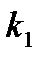 и
и 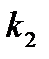 — действительные и притом не равные между собой числа (
— действительные и притом не равные между собой числа ( 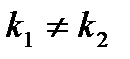 ). Тогда общее решение имеет вид
). Тогда общее решение имеет вид 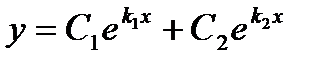 (3)
(3)
2. 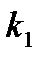 и
и 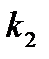 — комплексные числа
— комплексные числа
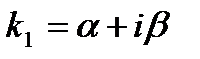 ,
, 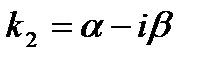 , где
, где 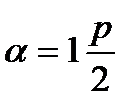 ,
, 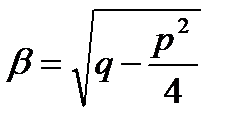
Общее решение имеет вид 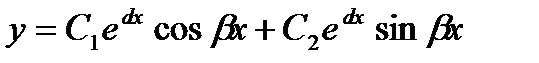 (4)
(4)
3. 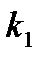 и
и 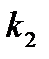 — действительные равные числа (
— действительные равные числа ( 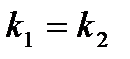 ).
).
Общее решение имеет вид 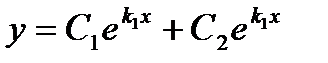 (5)
(5)
Пример 9.1. Решить уравнение
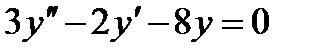
Решение. Характеристическое уравнение
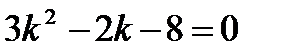
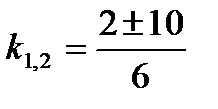 ;
; 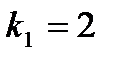 ,
, 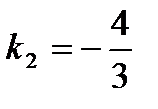
Общее решение 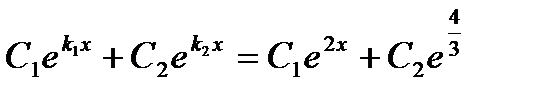
Пример 9.2. Решить уравнение
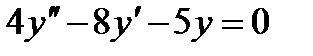
Решение
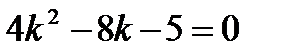
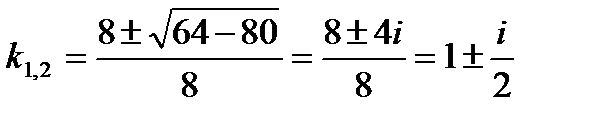 ;
; 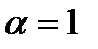 ,
, 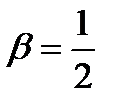
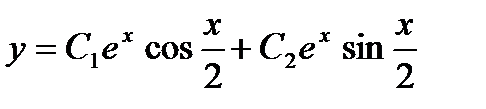
10. Неоднородные линейные уравнения 2-ого порядка с постоянными коэффициентами.
Это уравнение вида
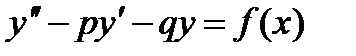 (1)
(1)
Сводная таблица видов частных решений для различных видов правых частей.
| № | Правая часть дифференциальных уравнений | Корни характеристического уравнения | Виды частного решения |
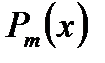  | 1. Число 0 не является корнем характеристического уравнения. | 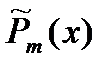 | |
| 2. Число 0 — корень характеристического уравнения кратного S. | 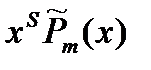 | ||
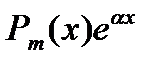 | 1. Число 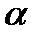 не является корнем характерного уравнения. не является корнем характерного уравнения. | 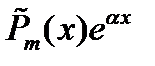 | |
2. Число 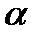 является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S. | 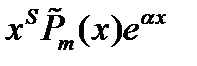 | ||
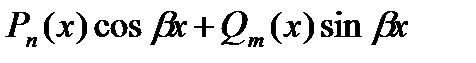 | 1. Число 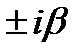 не является корнем характерного уравнения. не является корнем характерного уравнения. | 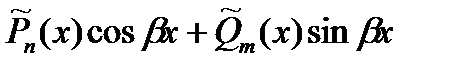 | |
2. Число 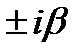 является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S. | 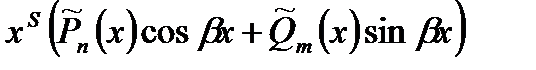 | ||
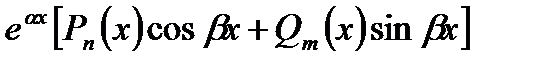 | 1. Число 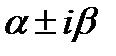 не является корнем характерного уравнения. не является корнем характерного уравнения. | 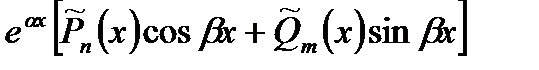 | |
2. Число 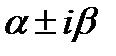 является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S. | 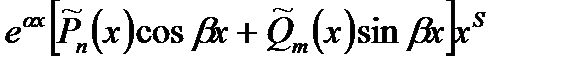 |
Пример 10.1. Решить уравнение
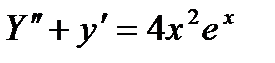
Решение. Характеристическое уравнение
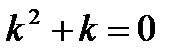
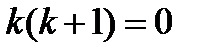 ,
, 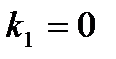 ,
, 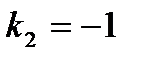
Общее решение однородных уравнений имеет вид: 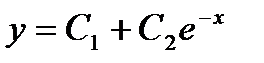
Правая часть уравнения 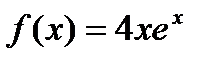 ,
, 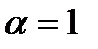 т.к.
т.к. 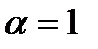 не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
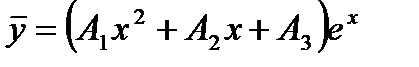
Подставляя его в исходное уравнение и сокращая обе части уравнения на 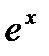 , будем иметь
, будем иметь
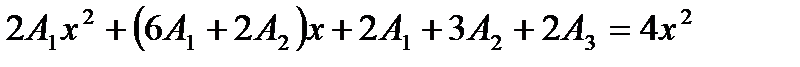
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства, получаем линейную систему уравнений для нахождения коэффициентов 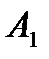 ,
, 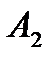 и
и 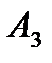 :
:
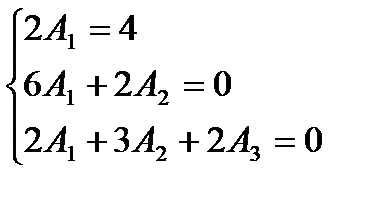
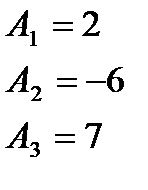
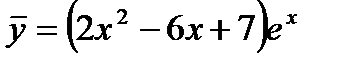
Общее решение данного уравнения 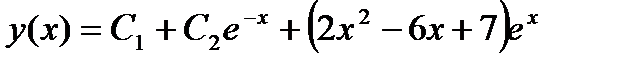
Пример 10.2. Найти общее решение уравнения
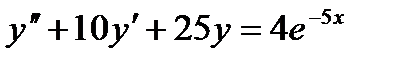
Решение: характеристическое уравнение k2+ 10k + 25=0 имеет двукратный корень k1 = k2=-5, поэтому y= (C1 +C2 x ) e-5x.
Т. к. к=-5 является корнем характеристического уравнения кратности s=2, то частное решение неоднородного уравнения ищем в виде ( см. табл., случай 2(2)):

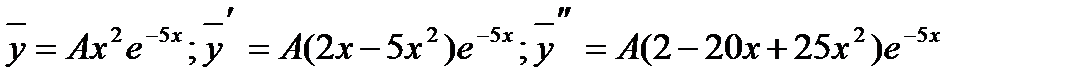
Подставляя выражения для y,y! ,y”в исходное уравнение, получаем
2Ae-5x =4e-5x, A=2, y = 2x2e-5x. Общее решение данного уравнения

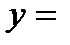
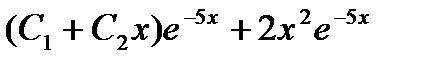
Пример 10.3 Найти частное решение уравнения

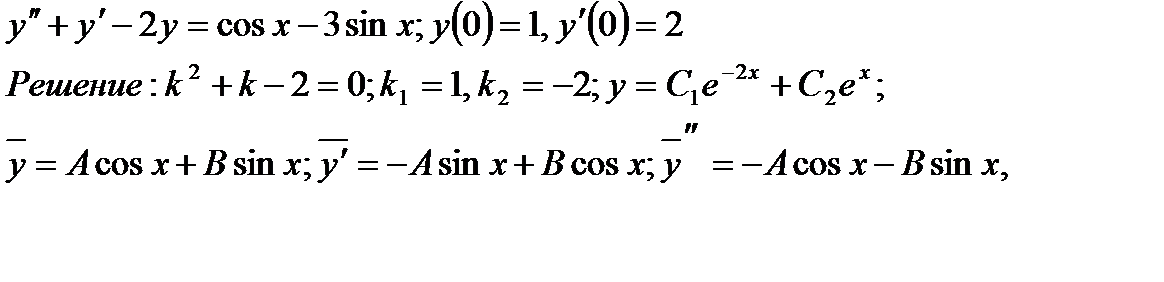
Подставляя выражения для y,y! ,y”в исходное уравнение, получаем:
(B-3A) cosx +(-3B-A) sinx = cosx –3 sinx,
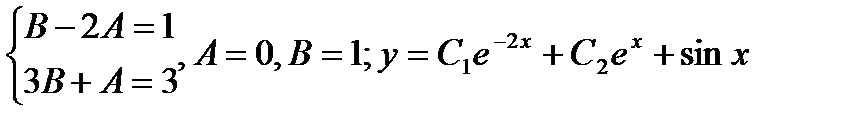
Найдем С1 и С2 , используя начальные условия:
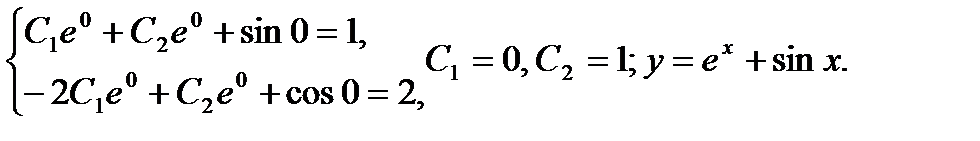
Пример 10.4. Решить уравнение:
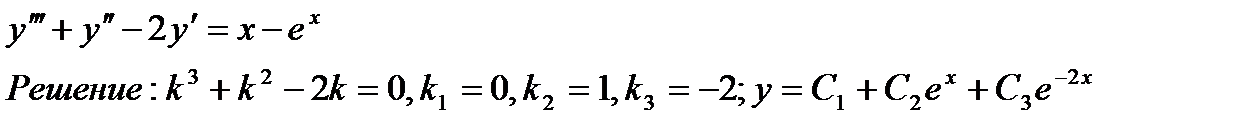
т. к. 0- простой корень характеристического уравнения, т.е.s=1, то частное решение ищем в виде:
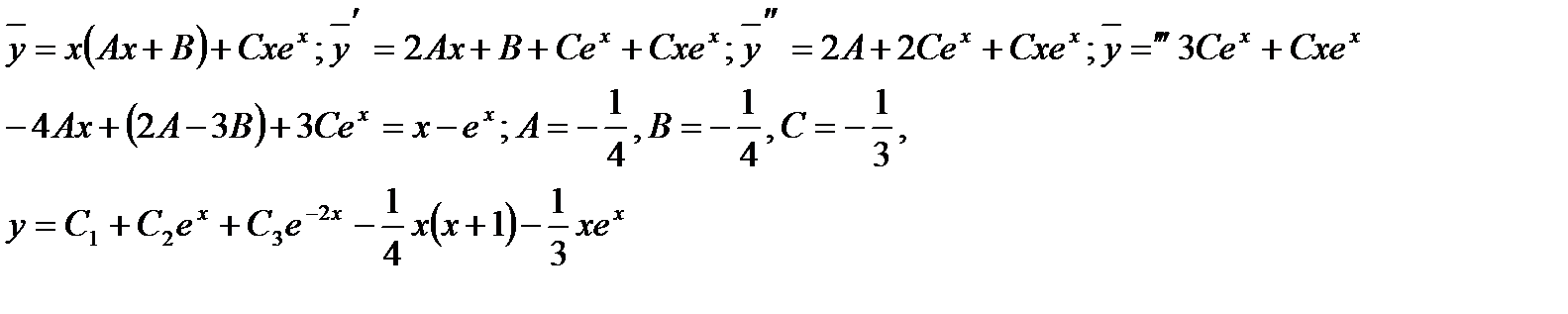
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Решить уравнения:
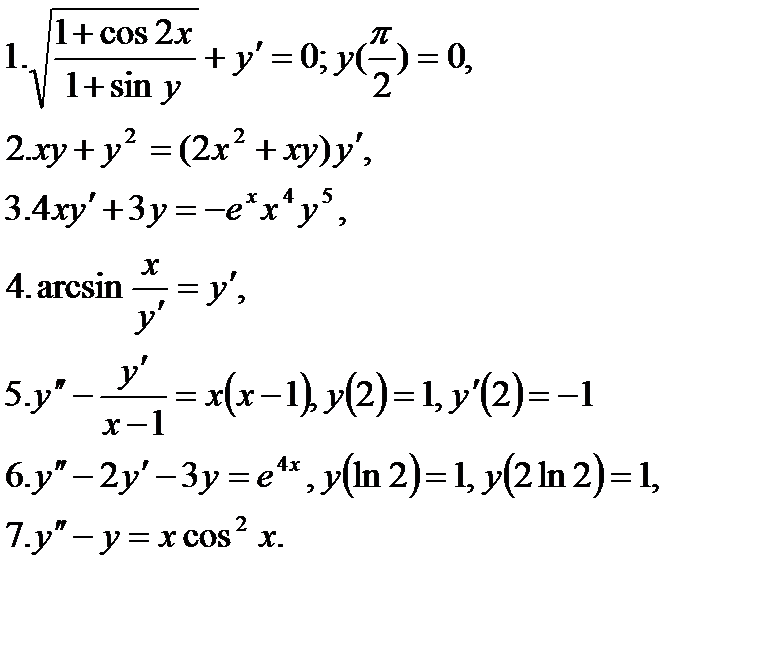
8. За 30 дней распалось 50 % первоначального количества радиоактивного вещества. Через сколько времени останется 1 % от первоначального количества?
( Закон радиоактивного распада: количество радиоактивного вещества, распадающегося за единицу времени, пропорционально количеству этого вещества, имеющегося в рассматриваемый момент).
9. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы касания.
Ответы:
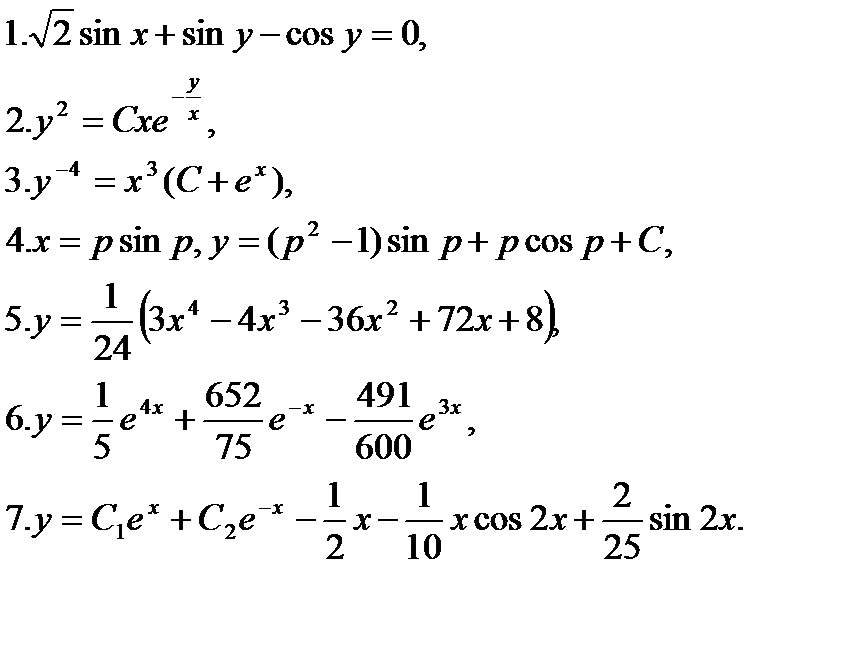
8. »200 дней.
9.y=Cx2.
