Билет 19. Классификация бесконечно малых функций.

Пусть при x→a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.

1. 
   Если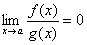 , то f(x) называется бесконечно малой высшего порядка, чем g(x) (относительно g(x)).
2. 
   Если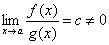 , то функции f(x) и g(x) называются бесконечно малыми одногопорядка.
3. 
   Если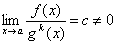 , то f(x) называется бесконечно малой k-го порядка относительноg(x).

Если 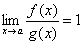, то функции f(x) и g(x) называются эквивалентными бесконечно малыми. В этом случае обе функции стремятся к нулю примерно с одинаковой скоростью. Эквивалентные бесконечно малые будем обозначать f ≈ g.

Примеры.

1. 
   Пусть f(x)=x²,g(x)=5x. Функции являются бесконечно малыми при x→0. Найдем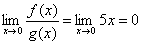 . Следовательно, f(x) – бесконечно малая высшего порядка относительно g(x).
2. 
   Пусть f(x)=x²–4,g(x)=x²–5x+6 – бесконечно малые при x→2.

.

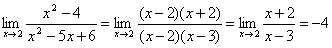Поэтому f(x) и g(x) одного порядка.

1. 
   f(x)=tg2x,g(x) = 2x – бесконечно малые при х→0.

.

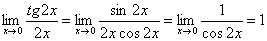Следовательно, f ≈ g.

1. 
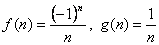   – бесконечно малые при n→∞.

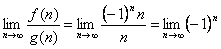– этот предел не существует. Поэтому говорят, что функции f и g не сравнимы.

При вычислении пределов полезно помнить о следующем свойстве эквивалентных бесконечно малых функций.

Теорема. Пусть f и g – бесконечно малые функции при х→а. Если 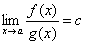и f ≈ f₁, g ≈ g₁, то 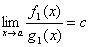, т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.

Доказательство. Имеем 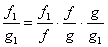. Тогда

,

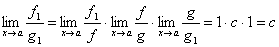что и требовалось доказать.

Примеры.

1. 
   .

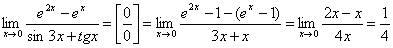Билет 20.

Непрерывные функции и их свойства. Точка разрыва функций и их классификация.

Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке:

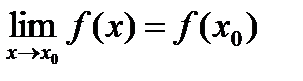
Это означает:

- функция определена в точке х₀ и в ее окрестности;

- функция имеет предел при х→х₀

- предел функции в точке х₀ равен значению функции в этой точке, т.е. выполняется равенство.

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х₀

Точки разрыва функции – это точки в которых нарушается непрерывность функции.

Точка разрыва х₀ называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)

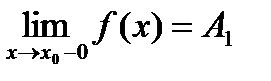и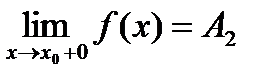

При этом, если:

- А₁=А₂ то точка х₀ называется точкой устранимого разрыва;

- А1≠А2 то точка х0 называется точкой конечного разрыва.

|A1 – A2| называется скачком функции.

Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.

Теоремы о непрерывности монотонной функции

Если ф-ииf(x)bg(x) определены на одном и том же промежутке[a,b]и обе непрерывны в т. Хо,тогда в этой точке непрерывными будут ф-ииf(x)+-g(x),f(x)*g(x),f(x)/g(x),lim(f(x)+-g(x))=limf(x)+-limg(x)