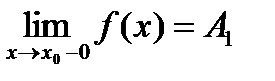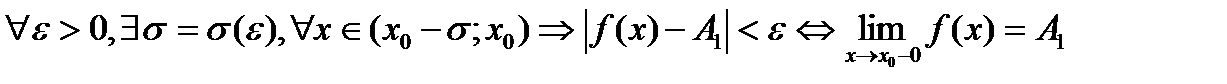Т е о р е м а 1. Если последовательность действительных чисел

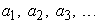(1)

не убывает (не возрастает) и ограничена сверху (снизу) числом 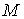(соответственно 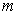), то существует действительное число 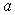, не превышающее 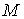(не меньшее 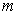), к которому эта последовательность стремится как к своему пределу:

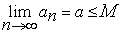(2)

(соответственно ).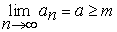

Д о к а з а т е л ь с т в о. Пусть последовательность (1) не убывает и пусть пока 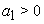, тогда и все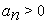 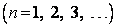. Каждый элемент последовательности разложим в бесконечную разложим в бесконечную десятичную дробь:

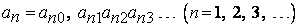. (3)

Так как последовательность 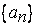ограничена сверху числом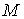 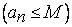и не убывает, то на основании леммы 2 § 1.6, десятичные дроби (3) стабилизируются к некоторому числу :

,

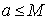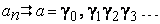но тогда 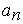стремится к 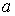как к своему пределу:

.

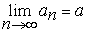В самом деле, для любого 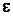найдется натуральное 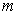такое, что 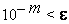. Так как 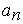стабилизируется к 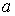, то

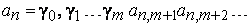
для всех 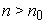, где 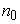достаточно велико, но тогда

,

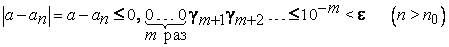т. е. 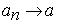при .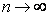

Если 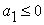, то прибавим к 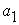число 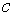настолько большое, что 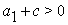, и положим .

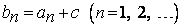Последовательность 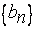не убывает, ограничена сверху числом 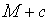и ее элементы положительны. Поэтому, по доказанному выше существует предел 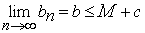, но тогда существует также предел 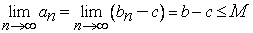, и теорема доказана для произвольной неубывающей последовательности.

Если теперь последовательность 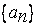не возрастает и ограничена снизу числом 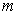, то последовательность чисел 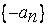не убывает и ограничена сверху числом 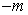, и, на основании уже доказанного, существует предел 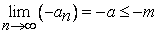, который мы обозначили через 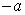. Следовательно, существует также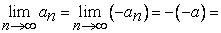 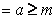. Теорема доказана.

З а м е ч а н и е. Если последовательность действительных чисел 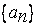сходится, то их десятичные разложения не обязательно стабилизируются. Например, если

,

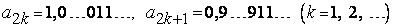где после запятой стоят 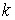нулей или 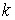девяток, то последовательность 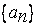имеет предел, равный 1 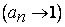, однако, как легко видеть, эта последовательность не стабилизируется.

Билет 17. Точка сгущения. Предел функции. Односторонние пределы. Свойства пределов. Монотонные функции.

Точка сгущения.Точка х0 называется точкой сгущения множества Х, если в любой проколотой окрестности точки х0 находится хотя бы элемент данного множества Х. Можно показать, что в любой окрестности точки сгущения находится бесконечное множество элементов Х. точка сгущения может принадлежать множеству, но может ему и не принадлежать.

Число А называется пределом функции y=f(x) в точке х₀, если для любой последовательности допустимых значений аргумента x_n, n?N (x_n≠x₀), сходящейся к х₀

(т.е. 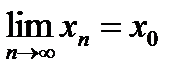), последовательность соответствующих значений функции f(x_n), n?N, сходится к числу А, т.е. 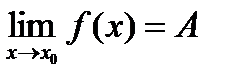. Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х₀, соответствующие значения функции как угодно мало отличается от числа А.

Односторонние пределы.

Считается, что х стремится к х₀ любым способом: оставаясь меньшим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х₀.

Число А₁ называется пределом функции y=f(x) слева в точке х₀, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х?(x₀-σ;x₀), выполняется неравенство |f(x)-A₁|<ε