Тригонометрическая запись комплексного числа

Модуль и комплексного числа 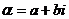связаны с его компонентами при помощи формул , . Эти формулы следуют непосредственно из определения функций и любого угла. Ясно, что , , . Эти формулы определяют модуль и аргумент по данным 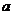и b. Для определения аргумента можно пользоваться формулой при . Однако эта формула задает 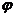лишь с точностью до целого кратного (т.е. полуоборота), а не до целого кратного .

Подставляя вместо компонент комплексного числа 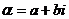их выражения через модуль и аргумент получаем .

Такая форма записи комплексного числа называется тригонометрической.

Примеры:

, где .

Умножение комплексных чисел в тригонометрической форме

Пусть и , тогда легко проверить, что .

Следовательно, модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей. В буквенной записи , .

Это правило распространяется на произведение любого числа сомножителей. Именно, , . Если мы будем перемножать несколько раз одно и тоже число, то получим

. При r = 1 получается знаменитая формула Муавра: .

. Формула верна не только для натуральных значений k, но и для всех целых значений.

Деление комплексного числа в тригонометрической форме

Пусть , тогда

.

Если , то .

Следовательно, модуль частного двух комплексных чисел равен частному их модулей, а аргумент частного равен разности аргументов. В буквенной записи: , .

Извлечение корня из комплексного числа

Пусть n – натуральное число. Извлечь корень с показателем n из комплексного числа 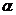- это значит найти комплексное число (или числа) 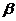так, что . Каждое число 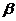такое, что - называется корнем n – й степени из 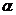и обозначается . Ясно, что если , то единственным значением является число 0, поэтому сосредоточим внимание на случае .

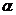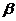Запишем в тригонометрической форме: и будем искать тоже в тригонометрической записи: . Равенство запишется в виде .

Приравнивая модули и аргументы (с учетом многозначности), получим, что последнее равенство равносильно равенствам:

и

Данное r – положительно ( ) и искомое R тоже должно быть положительно. Известно, что для любого положительного числа существует единственное значение корня n –ой степени, называемое арифметическим значением корня, т.е. . Аргумент же Q находится просто делением .

Таким образом, корни n- ой степени из комплексного числа 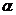существуют, и все они получаются по формуле:

(1) .

В формуле (1) 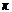- любое целое число, но однако достаточно ограничиться значениями . Действительно, пусть , . Разделим 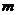на 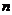с остатком: , где - целое число, а остаток 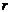может принимать только такие значения: 0, 1, …, .

Так как

, ,

то , где . Итак, мы доказали теорему:

Теорема 1:Существует ровно n корней 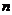- ой степени из комплексного числа . Они вычисляются по формуле (1) при .

Пример: Вычислить .

, ,

следовательно, .

;

.