Понятие первообразной и неопределённого интеграла.

Определение 1: Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x)выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx

Определение 2: Множество F(x) + C всех первообразных функций для данной функции f (x) , где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом

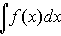
Таким образом, по определению,

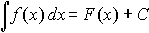
где F'(x) = f (x) или dF(x) = f(x)dx и С - произвольная постоянная. В последней формуле f(x) называется подинтегральной функцией, f(x)dx -подинтегральным выражением, а символ 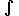- знаком неопределенного интеграла.
Неопределенным интегралом называют не только множество всех первообразных, но и любую функцию этого множества.

Свойства неопределённого интеграла.

1. 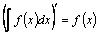; 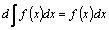–производная неопределенного интеграла равна подынтегральной функции, а его дифференциал–подынтегральному выражению.

2. 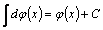– неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.

3. 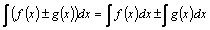–неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от этих функций.

4. 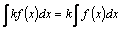, где k=const–постоянный множитель можно вынести за знак неопределенного интеграла.

Таблица интегралов.

1.		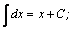11.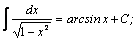
2.		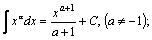12.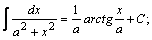
3.		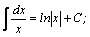13.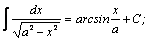
4.		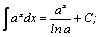14.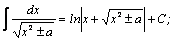
5.		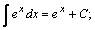15.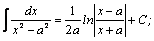
6.		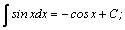16.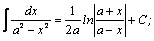
7.		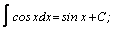17.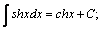
8.		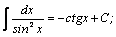18.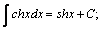
9.		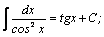19.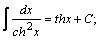
10.		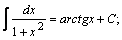20.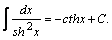

Формулы замены переменной и интегрирования по частям.

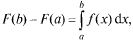Формула замены переменной.

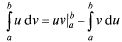Интегрирование по частям.

40,41,42,43,44,45)Есть в тетради в лекции «интегрирование функций содержащих выражение ax^2+bx+c.

Интегрирование иррациональных Функций.

Для интегрирования иррациональной функции, содержащей 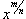используется подстановка .

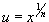Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме 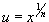, где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.

Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида 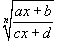, интегрируется с помощью подстановки .

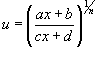Интегрирование Тригонометрических Функций.

1°. Интегралы вида

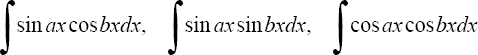
находятся с помощью тригонометрических формул

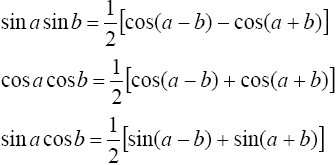
2°. Интегралы вида

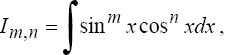
где m и n - четные числа находятся с помощью формул понижения степени

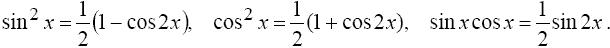
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

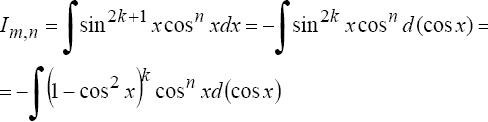
3°. Если m = -m, n = -l - целые отрицательные числа одинаковой четности, то

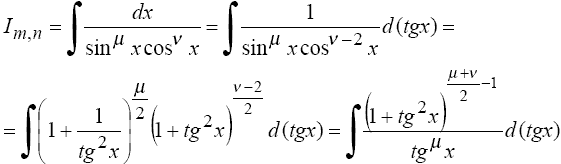
В частности, к этому случаю сводятся интегралы

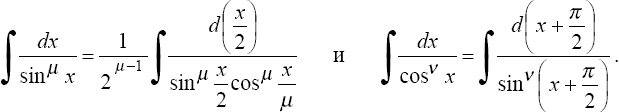
4°. Интегралы вида

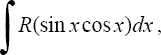
где R - рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки

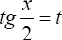
при этом

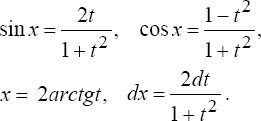
Если R{-sin x, cosx) = R(sinx, cosx), то целесообразно применить подстановку tgx = t. при этом

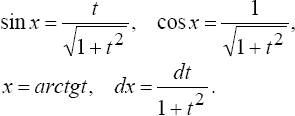
Определённый интеграл.

Пусть функция f(x) определена на отрезке [a, b]. Разобьем отрезок [a, b ] на n отрезков точками

x0 = a < x1 < … < xk − 1 < xk < … < xn − 1 < xn = b

и введем обозначения

Δxk = xk − xk − 1 (k = 1, …,n); λ =   max 1 ≤ k ≤ n Δxk.

На каждом отрезке [x _{k − 1}, x _k] выберем произвольным образом точку ξ_k (k = 1, …,n) и составим сумму

n ∑ k = 1 f(ξk) · Δxk ,

(5)

называемую (римановой) интегральной суммой функции f(x) на отрезке [a, b ].

Если существует конечный предел интегральных сумм (5) при λ → 0, причем этот предел не зависит ни от способа разбиения отрезка [a , b] на части, ни от выбора точек ξ_k, то функция f(x) называется интегрируемой (по Риману) на отрезке [a, b ], а указанный предел называется (римановым) определенным интегралом от f(x) по отрезку [a, b ] и обозначается символом

b ∫ a f(x) dx .

Таким образом,

b ∫ a f(x) dx = lim λ → 0 n ∑ k = 1 f(ξk) · Δxk .

Замечание. Данное Риманом определение интеграла оказалось неудачным. Современная терия интегрирования опирается на определение, данное Лебегом. Она гораздо более мощная и простая в применениях, чем теория Ремана.

3. Необходимое условие интегрируемости

Теорема 1. Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.

Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики : Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М. : Изд–во МЭИ, 2002. (Стр. 41.)

Замечание. Ограниченность функции не является достаточным условием ее интегрируемости.